Основные этапы эконометрического моделирования
Для описания сущности эконометрического моделирования удобно разбить весь процесс на шесть основных этапов:
1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли;
2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации, в частности, относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих;
3-й этап (параметризация) – собственно моделирование, т.е. выбор общего вида модели, в том числе состава и формы входящих в нее связей;
4-й этап (информационный) – сбор необходимой статистической информации, т.е. регистрация значений участвующих в модели факторов и показателей на различных временных или пространственных тактах функционирования изучаемого явления;
5-й этап (идентификация модели) – статистический анализ модели и в первую очередь статистическое оценивание неизвестных параметров модели;
6-й этап (верификация модели) – сопоставление реальных и модельных данных, проверка адекватности модели, оценка точности модельных данных.
Примеры спецификации и преобразования к приведенной форме моделей
Задача
1.
Требуется
составить спецификацию модели, которая
позволяет объяснять величину спроса
(
)
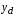и предложения (
)
товара, а также его рыночную цену (p)
величиной дохода (x)
на душу населения. При составлении
спецификации следует учесть известные
экономические законы:
-
спрос объясняется ценой товара и доходом на душу населения, причём уровень спроса падает с ростом цены и возрастает с увеличением дохода на душу населения;
2) предложение объясняется ценой товара и возрастает с ростом цены;
3) рыночная цена устанавливается при балансе спроса и предложения товара.
Первое уравнение именуется функцией спроса,
второе – функцией предложения,
третье – уравнением реакции рынка.
Задача 2. Выяснить экономический смысл коэффициентов a1, a2 и b1, входящих в структурную форму модели (1.1), и преобразовать её к приведённой форме.
Составим приведённую форму модели (1.1).
Подставим правые части первого и второго уравнения в третье:
a0 + a1 · p + a2 · x = b0 + b1 · p.
Представим переменную p как явную функцию переменной x:
p = (a0 – b0)/(b1 – a1 ) + (a2 /(b1 – a1 )) · x
yd = (a0 · b1 – b0 · a1 )/( b1 – a1) + (a2 · b1 /( b1 – a1 )) · x,
ys = (a0 · b1 – b0 · a1 )/( b1 – a1) + (a2 · b1 /( b1 – a1 )) · x.
yd = α0 + α1 · x;
ys = α0 + α1 · x;
p = β0+ β1 · x.
α0 = (a0 · b1 – b0 · a1)/( b1 – a1),
α1 = a2 · b1 / (b1 – a1),
β0 = (a0 –b0)/ (b1 – a1),
β1 = a2 / (b1 – a1).
∆p = β1 · ∆x
∆yd = ∆ys = α1 · ∆x
∆yd = ∆ys = b1∙∆p,
Задача 3.
Требуется составить спецификацию модели, которая позволяет объяснять величину спроса (yd) на конкурентном рынке нормального товара значением его цены (p), уровнем душевого дохода потребителя (x) и фактором сезонности (кварталом года).
q1={1- для первого квартала, 0- для других кварталов};
q2={1- для второго квартала, 0 - для других кварталов};
q3={1- для третьего квартала, 0 - для других кварталов}.
Учитывая решение задачи 1, получаем
yd = a0 + a1 · p + a2 · x + b1∙q1 + b2∙q2 + b3∙q3,
a1 < 0, a2 >0.
Первый квартал
yd = (a0 + b1) + a1 · p + a2 · x
a1 < 0, a2 >0;
Четвёртый квартал
yd = a0 + a1 · p + a2 · x,
a1 < 0, a2 >0.