Пример.
Органы государственной статистики получают балансы предприятий, достоверность которых никто не подтверждает. Последующее обобщение информации может содержать ошибки измерения.
После выявления отдельных соотношений их группируют в модель.
Таким образом, методика построения эконометрических моделей может быть разбита на следующие этапы:
1.Спецификация модели.
2.Идентификация модели (статистическое оценивание параметров модели по выборочным данным).
3.Верификация моделей (проверка качества построенной модели).
Проверка качества в эконометрике происходит по двум направлениям:
а) оценивается статистическая значимость каждого параметра модели и происходит оценка случайной величины (ε).
б) оценка значимости уравнения в целом.
Математическая модель – упрощенно, формализованное представление реальности (объекта, явления, процесса), записанное в виде совокупности формул, преобразование которых осуществляется на основе правил логики и математики.
В экономической модели любого типа все участвующие в ней переменные разделяются на:
-
Экзогенные («внешние», автономные, в определенной степени управляемые, задаваемые извне);
-
Эндогенные (формулируются в процессе и «внутри» социально- экономической системы в большой мере под воздействием экзогенных переменных; взаимодействуют друг с другом; в эконометрической модели – объясняемые переменные);
-
Предопределенные (факторы - аргументы, объясняющие переменные)
Множество предопределенных переменных формируется из всех экзогенных переменных («привязанных» к прошлым, текущим и будущим моментам времени) и так называемых, лаговых эндогенных переменных - эндогенных переменных, значении которых уже вычислены в прошлые по отношению к текущему моменту времени, то есть уже известных, заданных.
Эконометрическая модель, следовательно, служит для объяснения поведения эндогенных (объясняемых) переменных в зависимости от значений экзогенных и лаговых эндогенных переменных.
При
построении и анализе эконометрических
моделей различают структурную и
приведенную формы. Пусть общее число
эндогенных переменных равно m,
а предопределенных n.
Примем, что общее число уравнений в
эконометрической модели равно числу
эндогенных переменных m.
Пусть из общего числа m
мы имеем
уравнений,
включающих случайные компоненты, и
тождеств
(
).
Введем
вектор эндогенных переменных
.
Разобьем его на два подвектора
и
.
Пусть
–
вектор-столбец предопределенных
переменных.
Общий вид линейной эконометрической модели для данного момента времени t выглядит следующим образом:
(2)
где
–
матрица размерности (
)
из коэффициентов при
в
первых
уравнениях,
– матрица размерности (
)
из коэффициентов при
в этих же
уравнениях,
,
-
вектор-столбец размерности (
)
случайных остаточных составляющих,
- вектор-столбец размерности (
),
состоящий из нулей.
Остальные матрицы определяются аналогично.
Все
элементы матриц
и
являются
известными (то есть их числовые значения
определяются содержательным смыслом
соответствующих тождеств системы).
Элементы матриц
определяются
по исходным статистическим данным.
Система (2) может быть записана в виде:
,
(3)
где
;
;
;
.
Система
уравнений вида (2) или (3) называется
структурной
формой
линейной эконометрической модели. При
этом предполагается, что коэффициент
k-ой
эндогенной (объясняемой) переменной в
k
–ом структурном стохастическом уравнении
(k=1,2,…,m)
равен
единице
(правило нормировки системы), матрицы
и
–
невырождены. Матрица В
на
главной диагонали имеет коэффициенты,
равные единице.
При
реализации конечных прикладных целей
эконометрического моделирования главный
интерес представляют соотношения,
позволяющие выразить все эндогенные
переменные
через
предопределенные
.
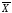Поэтому рассматривают также и приведенную
(редуцированную)
форму линейной модели. Умножим обе части
выражения (3) на обратную матрицу
,
получим
(4)
Или в другой записи:
,
(5)
где
,
.