1. Построение точечного прогноза и доверительного интервала для линейной факторной модели регрессии.

Прогнозируемое значение переменной у: ŷ прогн =a0+a1xпрогн

Данный прогноз называется точечным. Вероятность реализации точечного прогноза практически равна нулю, поэтому рассчитывается доверительный интервал прогноза с большой надёжностью.

Доверительные интервалы прогноза зависят от стандартной ошибки, удаления хпрогнот своего среднего значения ẋ, количества наблюденийnи уровня значимости прогноза α.

Доверительные интервалы прогноза: u(k)=tтабл*Sᶓ*,

где – определяется по таблице распределения Стьюдента для уровня значимости α и числа степеней свободы ϒ=n-k-1

2. Корреляция для нелинейной регрессии. Средняя ошибка аппроксимации.

3. Нелинейные модели регрессии, нелинейные по оцениваемым параметрам. Особенности использования этих моделей в экономических задачах.

Степенная функция:

*

Линеаризация: Для определения параметров степенной функции с помощью метода наименьших квадратов необходимо привести её к линейному виду путём логарифмирования обеих частей уравнения: . Это уравнение представляет собой прямую линию на графике, по осям которого откладываются не сами числа, а их логарифмы (так называемая логарифмическая шкала или логарифмическая сетка).

Пусть Y=X=,A=.

Тогда уравнение примет вид Y=A+X.

Параметры модели определяются по следующим формулам:

=;A=.

Показательная функция:

*

Линеаризация: Линеаризацию переменных проведём путём логарифмирования обеих частей уравнения:

Уравнение изображается прямой линией на полулогарифмической сетке, которая получается как сочетание натуральной шкалы для значений независимой переменной xи логарифмической шкалы – для значений зависимой переменнойy.

Пусть Y=,A=,B=.

Тогда уравнение примет вид Y=A+B.

Параметры модели определяются по следующим формулам:

;.

4. Нелинейные модели регрессии, линейные по оцениваемым параметрам. Особенности их использования.

Полином второго порядка:

Уравнение регрессии: ŷx=

Нормальные уравнения: n;

+++;

.

Гипербола:

Уравнение регрессии:

Нормальные уравнения:

n+;

.

Или заменим на новую переменнуюX. В результате получим линейное уравнение

Параметры определяются из следующих формул:

;

5. Линейная модель множественной регрессии, основные предположения. Метод наименьших квадратов, как основной метод оценивания параметров регрессии.

Из-за особенностей метода наименьших квадратов во множественной регрессии, как и в парной, применяются только линейные уравнения и уравнения, приводимые к линейному виду путём преобразования переменных. Причём из-за трудности обоснования формы связи чаще всего используется линейное уравнение, которое можно записать следующим образом: , где– параметры модели (коэффициенты регрессии);– случайная величина (величина остатка).

Коэффициент регрессии показывает, на какую величину в среднем изменится результативный признакy, если переменнуюувеличить на единицу измерения при фиксированном (постоянном) значении других факторов, входящих в уравнение регрессии.

Оценку параметров модели можно провести в матричной форме.

Y=Xa+ᶓ,

Где Y– вектор значений зависимой переменной размерности (n*1);

X– матрица значений независимых переменныхразмерность матрицыXравнаn*(k+1). Первый столбец является единичным, так как в уравнении регрессииумножается на единицу;

a– подлежащий оцениванию вектор неизвестных параметров размерности (k+1)*1;

ᶓ - вектор случайных отклонений размерности (n*1).

Y= ;X= ;a= .

Формула для вычисления параметров регрессионного уравнения по методу наименьших квадратов: A=

Где X’ – транспонированная матрицаX;

– Обратная матрица.

Оценивание достоверности каждого из параметров модели осуществляется при помощи t-критерия Стьюдента. Для любого из параметров моделизначениеt-критерия рассчитывается по формуле:

Где - стандартное (среднее квадратическое) отклонение уравнения регресси. Оно определяется по формуле.

– диагональные элементы матрицы.

Коэффициент регрессиисчитается достаточно надёжным, если расчётное значениеt-критерия с (n-k-1) степенями свободы превышает табличное, т.е.

Если надёжность коэффициента регрессии не подтверждается, то следует вывод о несущественности в модели факторного j-го признака и необходимости его устранения из модели или замены на другой факторный признак.

6. Парная регрессия. Оценка значимости отдельных параметров уравнения регрессии.

Оценка статистической значимости параметров модели

После определения параметров модели на основе МНК, требуется проведение этапа верификации модели (проверки качества), который обязательно включает проверку статистической значимости параметров, проверку общего качества модели, проверку точности модели

При проверке качества модели необходимо, прежде всего, проверить наличие линейной связи между и, т.е. проверить статистическую значимость параметраДанный анализ, как уже говорилось, осуществляется по схеме статистической проверки гипотез. Формулируется две гипотезы:

H₀:

H₁:

Рассчитывается t–статистика:

Можно доказать (доказательство опускаем), что вычисляется по формуле:

, (2.12)

здесь - стандартное отклонение случайной величиныb.

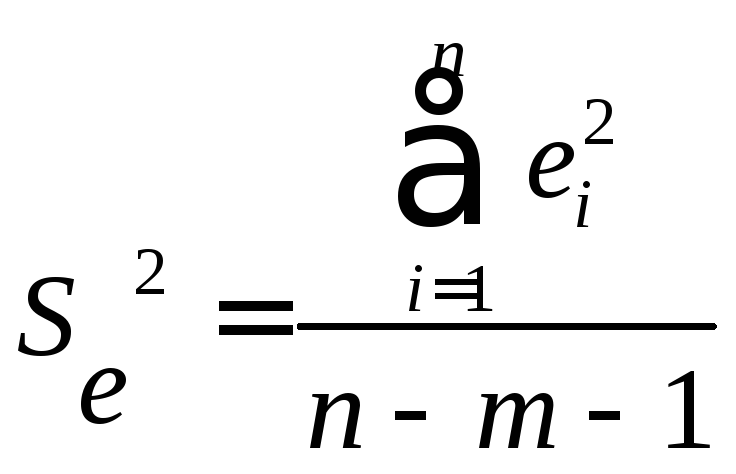–остаточная оценочная дисперсия (оценка дисперсии ошибок), а n- число наблюдений, m–число переменных модели

Величина b есть мера наклона линии регрессии. Очевидно, что чем больше разброс значений Y вокруг линии регрессии (больше), тем больше (в среднем) ошибка в определении наклона линии регрессии. Если такого разброса нет совсем (_i=0, следовательно, =0), то прямая определяется однозначно и ошибок в определении параметров нет.

Знаменатель величины зависит от диапазона изменения переменной X. Чем шире этот диапазон, тем больше и меньше ошибка в оценке величины наклона прямой. Кроме того, увеличение числа наблюдений (при прочих равных условиях) также увеличивает и, следовательно, уменьшает величину ошибки.

Если (расчетное значение статистики) будет больше теоретического ( t), то нулевая гипотеза отклоняется, а коэффициентb признается статистически значимым с выбранным уровнем доверия. В этом случае для коэффициента b можно построить доверительный интервал:

. (2.13)

Если нулевая гипотеза принимается (b=0), то это свидетельствует об отсутствии связи между зависимой и факторной переменными.

По аналогичной схеме проверяется гипотеза о статистической значимости коэффициента a:

=(2.14),

здесь и- стандартные отклонения случайных величинa и b.

Дисперсия свободного члена уравнения пропорциональна,поэтому для нее справедливы уже сделанные пояснения о влиянии разбросавокруг регрессионной прямой и разброса на стандартную ошибку.

Чем сильнее меняется наклон прямой, проведенной через данную точку , тем больше разброс свободного члена, характеризующего точку пересечения этой прямой с осью Y.

Кроме того, дисперсия и стандартная ошибка свободного члена тем больше, чем больше средняя величина. При больших по модулю значениях X даже небольшое изменение наклона регрессионной прямой может вызвать большое изменение свободного члена, поскольку в этом случае велико расстояние от точек наблюдений до оси Y.

7. Парная регрессия. Оценка значимости уравнения регрессии.

Классическая линейная модель парной регрессии

Вычисление оценок МНК не требует, вообще-то говоря, введения каких-либо дополнительных гипотез. Сам метод часто рассматривают как способ «разумного» выравнивания эмпирических данных.

В то же время оценки , вычисленные по МНК, не позволяют сделать вывод, насколько близки найденные значения параметров к своим теоретическим прототипами насколько надежны найденные оценки. Поэтому для оценки адекватности модели и ее прогностической способности необходимо введение дополнительных предположений. Можно показать, что о свойствах параметровможно судить лишь, если наложены определенные условия на реализации случайного члена.

В классической модели линейной регрессии делаются следующие четыре предположения (условия Гаусса–Маркова):

1. Математическое ожидание случайного отклонения равно нулю для всех наблюдений:, i = 1,2,…,n,

Данное условие означает, что случайное отклонение в среднем не оказывает влияния на зависимую переменную. В каждом наблюдении случайный член может быть либо положительным, либо отрицательным, но он не должен иметь систематического смещения. Отметим, что выполнимость влечет выполнимость

0. Дисперсия постоянна для всех наблюдений:дляi = 1,2,…,n, причем ее величина неизвестна. Одной из задач регрессионного анализа является оценка(стандартного отклонения). Данное условие подразумевает, что, не смотря на то, что в каждом конкретном наблюдении случайное отклонение может быть различно, не должно быть некой априорной величины, вызывающей большую ошибку. Выполнимость этого предположения называется гомоскедастичностью (постоянством дисперсии отклонений), невыполнимость этого предположения называется гетероскедастичностью (непостоянством дисперсии отклонений).

1. Случайные отклонения во всех наблюдениях должны быть независимы друг от друга, т. е. отсутствует систематическая связь между любыми случайными отклонениями. Это условие, в частности, означает, что

0. Случайные отклонения должны быть распределены независимо от объясняющих переменных. Обычно это условие выполняется автоматически, если в качестве факторной переменной рассматривается не случайная величина.

Перечисленные свойства не зависят от конкретного вида распределения величин _i, тем не менее, обычно предполагается, что они распределены нормально. Эта предпосылка необходима для проверки статистических гипотез и построения доверительных интервалов.

Если условия Гаусса–Маркова для случайного члена выполняются, то оценки, найденные по МНК определяют адекватную и надежную модель. Для проверки выполнения перечисленных свойств имеются специальные статистические критерии.