19. Анализ линейной и нелинейных моделей.

	Уравнение	R2	F	Aср.	Эср.
Линейная	у=0,9378х+54,059	0,6784	21,09842966	0,045583496	0,600793119
Степенная	у=8,7252х0,614532	0,662	17,5349	0,04730261	0,614532
Показательная	у=75,9820,0066х	0,6578	20,3316283	0,04586123	0,57250843
Равносторонняя гипербола	у=226,336462+(-7743,59071/х)	0,66252429	19,6317625	0,047462265	0,65120909

Лучшей является линейнаямодель, по ней мы будем осуществлять расчеты.

Расчеты, выполненные для степенной модели.

Приводим к линейному виду:

ln=lna+b•lnx

Производим замену:

ln= z , ln a=c, ln x=t

z=c+bt

b=, c=

b=0,6145

c=2,1662

z=2,1662+0,6145·t

ln y = 2,1662+0,6145·ln x

= 8,7251•(x^(0,61))

Индекс корреляции:

=0,662

Сила связи заметная.

F-критерий:

F==17,5349

Ошибка аппроксимации:

=1/n•∑׀(y_i-y_т)/y_i ׀ •100%

=0,0473•100%=4,7%

Модель является точной

Коэффициент эластичности:

Э==0,6145

Расчеты, выполненные для показательной модели.

Приводим к линейному виду.

ln=lna•

ln=lna+xlnb

Производим замену:

ln=z , ln a=c, ln b=d

z=c+dx

d=, c=

d= 0,00659952

c= 4,33049657

z=4,33049657+0,00659952x

=

=е^4,33049657•e^{(0,00659952)^x}

Индекс корреляции:

= 0,81872531

Сила связи высокая.

F-критерий:

F=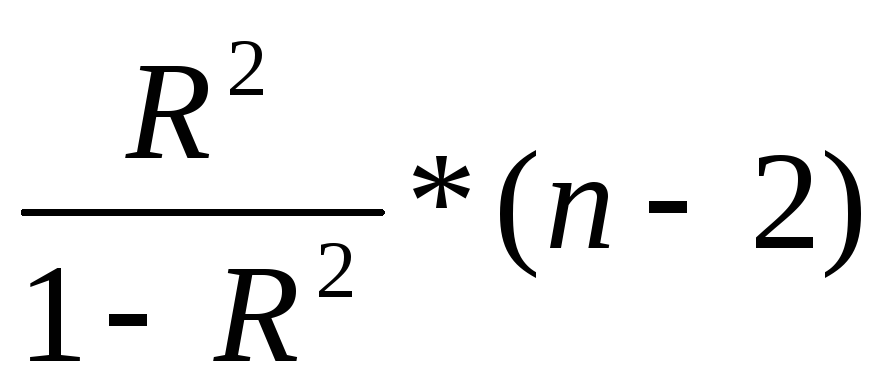=20,3316283

Ошибка аппроксимации:

=1/n•∑׀(y_i-y_т)/y_i ׀ •100%

= 0,04586123•100%= 4,5%

Модель является точной

Коэфф. эластичности:

Э== 0,57250843

Расчеты, выполненные для равносторонней гиперболы.

=a+

Произведем замену:

=a+bw

b=

a=

b=-7743,59071

а= 226,336462

=(-7743,59071)+226,336462,10/x

Индекс корреляции:

=0,81395595

Сила связи высокая.

F-критерий:

F== 19,6317625

Ошибка аппроксимации:

=1/n•∑׀(y_i-y_т)/y_i ׀ •100%

= 0,047462265•100%= 4,7%

Модель является удовлетворительной

Коэфф. эластичности:

Э= 0,65120909