
Вся эконометрика / Вся эконометрика / эконометрика 2 тихо / эконометрика шпоры
.doc
|
Билет 5 1. Типы переменных в эконометрических моделях и их назначение. Эндогенные переменные, экзогенные переменные, предопределенные переменные, лаговые переменные, фиктивные переменные, переменные - заместители. Переменные делятся на эндогенные и экзогенные, лаговые, предопределенные, фиктивные и переменные-заместители. Эндогенные переменные - переменные, объясняемые данной моделью, определенные в ней. Экзогенные – предопределенные переменные, влияющие на эндогенные, но не зависящие от них. Они принимаются извне. Переменные, значения которых в периоде t известны, называются предопределенными. Они выступают в роли факторов-аргументов или объясняющими переменными. Лаговыми переменными называют временные ряды факторных переменных, сдвинутые на один или более моментов времени. Они входят в уравнения анализируемой эконометрической системы, но измерены в прошлые моменты, а следовательно, являются уже известными, заданными Фиктивные вводятся для описания явления, в отношении которого нет данных по качественному признаку. Переменные-заместители искусственно вводятся в модель для отражения явления, кот не может быть количественно охарактеризовано, при этом эта переменная тесно коррелирует с этим явлением. |
|
2 Двухшаговый метод наименьших квадратов. Основная идея ДМНК — на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения. Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Метод получил название двухшагового МНК, ибо дважды используется МНК: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной: ŷi=δi1x1 + δi2x2+…+ δijxj и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных. Сверхидентифицируемая структурная модель может быть двух типов:
Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений. Применим ДМНК к простейшей сверхидентифицируемой модели:
Данная модель может быть получена из предыдущей идентифицируемой модели:
если наложить ограничения на ее параметры, а именно: b12 =a11 В результате первое уравнение стало сверхидентифицируемым: Н=1 (у1), D=1(х2) и D+1 > Н. Второе уравнение не изменилось и является точно идентифицируемым: Н = 2 и D=1 На первом шаге найдем приведенную форму модели, а именно:
ДМНК является наиболее общим и широко распространенным методом решения системы одновременных уравнений. Несмотря на важность системы эконометрических уравнений, на практике часто не принимают во внимание некоторые взаимосвязи, применение традиционного МНК к одному или нескольким уравнениям также широко распространено в эконометрике. В частности, при построении производственных функций анализ спроса можно вести, используя обычный МНК.
|
|
Билет 6 1. Схема построения эконометрических моделей. Проблемы, решаемые при эконометрическом исследовании. Весь процесс эконометрического моделирования можно разбить на шесть основных этапов. 1-й этап (постановочный) - определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли; 2-й этап (априорный) - предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез; 3-й этап (параметризация) - собственно моделирование, т.е. выбор общего вида модели, в том числе состава и формы входящих в неё связей между переменными; 4-й этап (информационный) - сбор необходимой статистической информации, т.е. регистрация значений участвующих в модели факторов и показателей; 5-й этап (идентификация модели) - статистический анализ модели и в первую очередь статистическое оценивание неизвестных параметров модели Непосредственно связан с проблемой идентифицируемости модели, то есть ответа на вопрос «Возможно ли в принципе однозначно восстановить значения неизвестных параметров модели по имеющимся исходным данным в соответст-вии с решением, принятым на этапе параметризации?». После положительного ответа на этот вопрос необходимо решить проблему идентификации модели то есть предложить и реализовать математически корректную процедуру оценивания неизвестных параметров модели по имеющимся исходным данным; 6-й этап (верификация модели) — сопоставление реальных и модельных данных, проверка адекватности модели, оценка точности модельных данных. Эконометрическое исследование включает решение следующих проблем
|
|
2. Косвенный метод наименьших квадратов. Процедура применения КМНК предполагает выполнение следующих этапов работ:
Пример: Приведенная форма модели, построенной на основе имеющихся данных, имеет вид:
где u1, u2 - случайные ошибки приведенной формы модели Для каждого уравнения приведенной формы модели применяет традиционный МНК и определяем δ-коэффициенты. Для первого уровня приведенной формы модели система нормальных уравнений составит:
для второго уровня:
Переходим от приведенной к структурной форме модели:
|
|
Билет 7 1. Принципы спецификации эконометрических моделей. Эконометрика – наука, дающая количественное выражение взаимосвязей экономических явлений и процессов. Основная цель: модельное описание конкретных количественных взаимосвязей, обусловленных общими качественными закономерностями, изученными в экономической теории. Модель – это такой материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает новые знания об объекте-оригинале. Она выступает в качестве средства анализа и прогнозирования конкретных экономических процессов на основе реальной статистической информации. Необходимость использования метода моделирования определяется тем, что многие объекты (или проблемы, относящиеся к этим объектам) непосредственно исследовать или вовсе невозможно, или же это исследование требует много времени и средств. Выделяют 4 принципа построения спецификации эконометрической модели:
Экзогенные (независимые) переменные – экономические переменные объекта, значения которых определяются вне данной модели объекта. Эндогенные (зависимые) переменные – экономические переменные объекта, значения которых определяются внутри модели в результате одновременного взаимодействия образующих модель соотношений.
Y t Xt Yt-1 ,…, Yt-n – прошлое Yt+1 ,…, Yt+n - будущее
|
|
2. Назначение фиктивных переменных. Спецификация и оценивание модели с фиктивными переменными. Может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть разного рода атрибутивные признаки. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены цифровые значения. Такого рода переменные принято называть фиктивными переменными. Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается зависимость потребления кофе у от цены х. В общем виде уравнение регрессии имеет вид: y=a+b*x+ε. Отдельно для лиц муж пола: y1=a1+b1*x1+ε1. Для жен: y2=a2+b2*x2+ε2 Объединив эти уравнения и введя фиктивные переменные (например пол) получим следующее выражение: y=a1*z1+a2*z2+b*x+ε, где z1 и z2 фиктивные переменные. В общем уравнении регрессии зависимая переменная у рассматривается как функция не только цены х, но и пола (z1, z2). Переменная z принимает всего два значения: 1 и 0. При этом когда z1 = 1, то z2 = 0 и, наоборот. Для лиц мужского пола, когда z1 = 1 и z2 = 0, объединена уравнение регрессии составит: ŷ = а1 + b·х, а для лиц женского пола, когда z1 = 0 и z2 = 1, ŷ =a2 + b·x. Иными словами, различия в потреблении для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии: а1 ≠ а2. Параметр b является общим для всей совокупности лиц как для мужчин, так и для женщин. Следует иметь в виду, что при введении фиктивных переменных в данную модель применение МНК для оценивания параметров а1 и а2, приведет к вырожденной матрице их оценок, и к невозможности получения их оценок. |
|
Билет 8 1. Классификация эконометрических моделей. По целевому назначению экономико-математические модели делятся на:
Экономико-математические модели могут предназначаться для исследования разных сторон народного хозяйства (производственно-технологической, территориальной) и его отдельных частей. При классификации моделей по исследуемым экономическим процессам и содержательной проблематике выделяются модели народного хозяйства в целом и его отдельных подсистем-отраслей, регионов и т.д., комплексы моделей производства, потребления, формирования и распределения доходов, трудовых ресурсов, ценообразования, финансовых связей и т. д. В исследованиях на народнохозяйственном уровне чаще применяются структурные или структурно-функциональные модели, поскольку для планирования и управления большое значение имеют взаимосвязи подсистем. Функциональные модели широко применяются в экономическом регулировании. Различают дескриптивные и нормативные модели. Дескриптивные модели объясняют наблюдаемые факты или дают вероятностный прогноз. Нормативные отвечают на вопрос: как это должно быть?, т. е. предполагают целенаправленную деятельность. Примером нормативной модели являются модели оптимального планирования, формализующие тем или иным способом цели экономического развития, возможности и средства их достижения. Примерами дескриптивных моделей являются производственные функции и функции покупательного спроса, построенные на основе обработки статистических данных. По характеру отражения причинно-следственных связей различают модели жестко детерминистские и модели, учитывающие случайность и неопределенность. В результате накопления опыта использования жестко детерминистских моделей были созданы реальные возможности успешного применения более совершенной методологии моделирования экономических процессов, учитывающих стохастику и неопределенность: проведение многовариантных расчетов и модельных экспериментов с вариацией конструкции модели и ее исходных данных; изучение устойчивости и надежности получаемых решений, выделение зоны неопределенности, включение в модель резервов; применение приемов, повышающих приспособляемость(адаптивность) экономических решений к вероятным и непредвиденным ситуациям. Получают распространение модели непосредственно отражающие стохастику и неопределенность экономических процессов и использующие соответствующий математический аппарат: теорию вероятностей и математическую статистику, теорию игр и статистических решений, теорию массового обслуживания, теорию случайных процессов. По способам отражения фактора времени экономико-математические модели делятся на: статистические и динамические. В статистических моделях все зависимости относятся к одному моменту времени. Динамические модели характеризуют изменение экономических процессов во времени. Общая классификация экономико-математических моделей включает более десяти основных признаков. С развитием экономико-математических исследований проблема классификации применяемых моделей усложняется. Наряду с появлением новых типов моделей (особенно смешанных типов) и новых признаков их классификаций, осуществляется процесс интеграции моделей разных типов в более сложные модельные конструкции. |
|
2. Проблема идентификации для эконометрических моделей в виде системы одновременных уравнений. При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификации – это единственность соответствия между приведенной и структурной формами модели. Проблема идентификации существует только для системы одновременных уравнений. Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметром структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема. Пример:
Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели. Пример
Модель содержит восемь структурных коэффициентов, что соответствует выражению п • (п — 1 + т).Структурная модель полном виде, содержащая п эндогенных и т предопределенных переменных в каждом уравнении системы, всегда неидентифицируема. Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. Пример:
Структурная модель всегда представляет собой систему сон местных уравнений, каждое из которых необходимо проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение. Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Для того чтобы уравнение было идентифицируемо, нужно, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного. |
|
Билет 9 1. Сбор статистических данных для оценивания параметров эконометрической модели. Сбор стат информации обусловлен наличием неизвестных коэффициентов в спецификации модели и заключается в сборе статистич данных об объекте – оригинале в виде конкретных значений эндогенных переменных и предопределенных переменных, входящих в спецификацию модели. Эта информация необходима для оценивания неизвестных коэффициентов, входящих в спецификацию модели. Сбор статистических данных (наблюдение) представляет собой процесс получения первичных данных об элементах исследуемой совокупности и их свойствах, которые становятся далее предметом статистической обработки и анализа. Основой любого статистического наблюдения является первичный статистический материал — фундамент эконометрического исследования, а задачей наблюдения является получение достоверной информации. Сбор статистических данных осуществляется главным образом посредством получения отчетности предприятий и организаций, а также путем проведения специального статистического наблюдения. Однако круг явлений рыночной экономики настолько велик, что полный охват отчетностью не только затруднителен, но и не всегда возможен. В таких случаях проводятся специальные обследования, статистические наблюдения. В эконометрике с точки зрения времени регистрации фактов различают текущее (непрерывное) и дискретное (прерывное), которое в свою очередь можно подразделить на единовременное, если наблюдение происходит от случая к случаю, и периодическое, если оно повторяется через определенные равные интервалы времени. В соответствии с охватом единиц наблюдаемого объекта различают сплошное и несплошное (выборочное) статистическое наблюдение. При сплошном наблюдении ставится задача получить сведения обо всех единицах изучаемой совокупности. К выборочному наблюдению прибегают в тех случаях, когда физически невозможно, трудно или нецелесообразно осуществить сплошное наблюдение, а также тогда, когда ограничения во времени или средствах не позволяют его осуществить. Несплошное наблюдение имеет свои разновидности: обследование основного массива, выборочное наблюдение, анкетное наблюдение и типическая монография. Обследование основного массива заключается в том, что наблюдение ведется за такой частью единиц объекта, которая является преобладающей в объеме исследуемого объекта. При выборочном наблюдении отбор подлежащих обследованию единиц изучаемого явления рыночной экономики организуют по принципу случайности: по жребию или механическим отбором, при котором обследуемые единицы выбирают в определенной последовательности. Сущность анкетного наблюдения заключается в том, что лицам, от которых необходимо получить сведения, рассылают анкеты с просьбой заполнить их и возвратить обратно. Типическая монография характеризуется тем, что в составе изучаемого явления выделяются однородные группы, состоящие из единиц одного типа. В каждой подлежащей обследованию группе подвергают наблюдению одну (иногда две, три) типичную единицу. Установленные при наблюдении величины признаков рассматривают как типичные (средние) величины для группы в целом. Программа наблюдения при типической монографии обычно бывает достаточно широкой, т. е. охватывает большое число признаков. |
|
2. Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели множественной регрессии
Множественная
регрессия
позволяет построить и проверить модель
линейной связи между зависимой
(эндогенной) и несколькими независимыми
(экзогенными) переменными: y
= f(x1,...,xр
), Линейное уравнение множественной корреляции: y=a+b1x1+b2x2+…+bpxp+ε Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии:
Для ее решения может быть применён метод определителей: a=∆a / ∆, b1=∆b1 / ∆,…, bp=∆bp / ∆,
∆a, ∆b1,…, ∆bp – частные определители; которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы. |
|
Билет 10 1. Оценивание параметров эконометрической модели. Понятие статистической процедуры оценивания параметров эконометрической модели. Требования к наилучшей статистической процедуре (состоятельность, несмещенность и минимальные дисперсии оценок параметров). Оценкой ân параметра a называют всякую функцию результатов наблюдений над случайной величиной X (иначе — статистику), с помощью которой судят о значениях параметра a. Статистические проверки параметров регрессии основаны на непроверяемых предпосылках распределения случайной величины. Они носят лишь предварительный характер. После построения уравнения регрессии проводится проверка наличия у оценок тех свойств, которые предполагались. Связано это с тем, что оценки параметров регрессии должны отвечать определенным критериям: быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют чрезвычайно важное практическое значение в использовании результатов регрессии и корреляции. В отличие от параметра, его оценка ã n — величина случайная. «Наилучшая оценка» ã n должна обладать наименьшим рассеянием относительно оцениваемого параметра a, например, наименьшей величиной математического ожидания квадрата отклонения оценки от оцениваемого параметра М(ã - a)2. Оценка â n параметра a называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т. е. М(ã) = a. В противном случае оценка называется смещенной. Если это равенство не выполняется, то оценка ã , полученная по разным выборкам, будет в среднем либо завышать значение a (если М(ã) > a , либо занижать его (если М(ã) < 0). Таким образом, требование несмещенности гарантирует отсутствие систематических ошибок при оценивании. Оценка â n параметра a называется состоятельной, если она удовлетворяет закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру:
В случае использования состоятельных оценок оправдывается увеличение объема выборки, так как при этом становятся маловероятными значительные ошибки при оценивании. Поэтому практический смысл имеют только состоятельные оценки. Несмещенная оценка ã n параметра a называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра a, вычисленных по выборкам одного и того же объема n.
Так
как для несмещенной оценки M(ã
n
- a)2
есть ее дисперсия
Для нахождения оценок параметров (характеристик) генеральной совокупности используется ряд методов. Указанные критерии оценок (несмещенность, состоятельность, эффективность) обязательно учитываются при разных способах оценивания. |
|
2. Логарифмическое преобразование эконометрической модели с нелинейным по коэффициентам уравнением регрессии (на примере эконометрической модели Кобба-Дугласа). Для преобразования нелинейной эконометрической модели Кобба – Дугласа к линейному виду необходимо воспользоваться операцией логарифмирования. Модель Кобба – Дугласа имеет следующий вид:
В результате логарифмирования получаем следующую систему уравнений (37.2):
Преобразовав получаем:
где yt=ln(Yt/Lt), b0=ln(a0), b1=a1, xt=ln(Kt/Lt), ut= ln(1+vt). Таким образом, yt – это логарифм производительности труда. Теперь уравнения наблюдения объекта образуют схему Гауса-Маркова : y(вектор)=X*b+ut , где X – это матрица, состоящая из значений вектора x, дополненных единицами. Коэффициенты b0 и b1 можно оценить МНК; параметр бu также оценивается МНК. Оценки a0 и a1 теперь определяются по оценкам: (~b0,~b1,~σu), а именно: a0=exp(~b0), ~a1=~b1 , ~σv=~σu при области определения параметра vt=(-1;+1). Итоги: при составлении эконометрических моделей со стандартными нелинейными по коэффициентам уравнениями регрессии следует случайные возмущения включать в модель в виде подходящего сомножителя, а затем преобразованием логарифмирования привести модель к линейной регрессии. После оценивания преобразованной модели следует вычислить оценки параметров исходной модели |





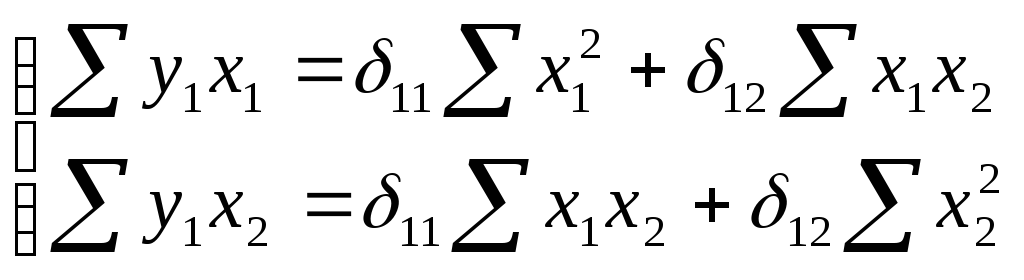





 где
у -
зависимая переменная (результативный
признак); х1,...,хр
- независимые
переменные (факторы).
где
у -
зависимая переменная (результативный
признак); х1,...,хр
- независимые
переменные (факторы).
 -
определитель системы
-
определитель системы

