11. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.

Выполнить прогноз заработной платы 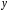при прогнозном значении среднедушевого прожиточного минимума , составляющем 107% от среднего уровня.

_{, где} - это 107% от среднего уровня значения среднедушевого прожиточного минимума

xp	94,33833333
ytxp	151,8603984

mytxp

1,042112077

интервал прогноза по линейному парному уравнению регрессии

149,538428

154,1823688

12. Найти доверительный интервал для индивидуальных значений зависимой переменной.

- индивидуальное значение среднедневной заработной платы, руб. (у)

my*

10,04971

дов интервал для индивидуальных значений зависимой переменной

129,4682388

129,4682388

13. Найти коэффициент эластичности.

Коэффициент эластичности показывает на сколько процентов в среднем по совокупности изменится среднедневная заработная плата, руб. (у) от своей средней величины при изменении среднедушевого прожиточного минимума в день одного трудоспособного, руб. ()

В общем случае:

Для линейной регрессии:

Эср

0,556481356

0,556481356

При изменении среднедушевого прожиточного минимума в день одного трудоспособного, руб. () на 1% среднедневная заработная плата, руб. (у) изменится на 0,556%.

14. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков ; построить график остатков.

e = y-yt

y	yt	у-yt
124	128,4843	-4,48427
145	133,0971	11,90293
152	137,7099	14,29013
133	141,4001	-8,40011
127	143,2452	-16,2452
138	146,0129	-8,01291
146	149,7031	-3,70315
159	150,6257	8,374294
155	151,5483	3,451734
153	154,3159	-1,31595
154	156,1611	-2,16106
168	161,6964	6,303576

Дисперсия

остаточная

90,65657435

15. Проверить выполнение предпосылок мнк.

15.1. Математическое ожидание остатков равно нулю.

сумма

8,53E-14

15.2. Дисперсия остатков постоянна

Для оценки на гомо- гетероскедастичность остаточной дисперсии воспользуемся методом Голдфельда-Квандта:

15.2.1. Упорядочим n наблюдений по мере возрастания среднедушевого прожиточного минимума в день одного трудоспособного, руб. ()

x	y
69	124
74	145
79	152
83	133
85	127
88	138
92	146
93	159
94	155
97	153
99	154
105	168

15.2.2. Разделим совокупность на две группы.

x	y
69	124
74	145
79	152
83	133
85	127
88	138

x	y
92	146
93	159
94	155
97	153
99	154
105	168

15.2.3. Определение остаточной суммы квадратов для первой регрессии и для второй по формуле:

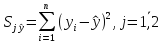
S1yt	764,6721944
S2yt	141,893549

15.2.4.Вычисляем соотношение

Fнабл

5,389055384

15.2.5. Рассчет критического значения F

Fкритич

5,050329058

Так как , то имеет место гетероскедастичность дисперсии, что приводит к ненадежности линейной модели данной регрессии.

15.3. В ряду остатков отсутствует существенная автокорреляция.

Ряд случайных величин называется автокоррелированным, если имеется корреляционная связь между последовательными значениями переменной в этом ряду.

Для проверки автокорреляции воспользуемся критерием Дарвина-Уотсона.

Рассчитаем d-статистику:

d-stat

1,326068615

Воспользуемся «схемой критерия». Так, как 1,32< 1,326068615<2, то уровень ряда остатков признается независимым.

15.4. Распределение остатков подчинено нормальному закону.

ННГУ им. Лобачевского

Отчет по лабораторной работе №2

по предмету эконометрика

«Нелинейная регрессия».

Работу выполнила

студентка 725гр.

Зотагина Анастасия

2011г

Модели разделяют на два класса нелинейности:

- регрессии, нелинейные относительно включенных в анализ объясняемых переменных, но линейные по оцениваемому параметру

- нелинейные по оцениваемому параметру

1. Степенная модель

1. Параметры уравнения степенной регрессии

y =

Необходимо линеаризовать модель (привести к линейному виду):

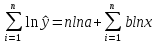
Произведем замену:

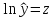
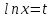
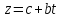
z=ln(y)	t=ln(x)
2,093422	1,838849
2,161368	1,869232
2,181844	1,897627
2,123852	1,919078
2,103804	1,929419
2,139879	1,944483
2,164353	1,963788
2,201397	1,968483
2,190332	1,973128
2,184691	1,986772
2,187521	1,995635
2,225309	2,021189

b	0,538144
c	1,117906

1.2. Степенная модель регрессии

Найдя параметры b и c, составим уравнение в линейном виде, выполнив его потенцирование, получим степенную модель.

y_тер
128,0773595
132,991107
137,7537421
141,464392
143,2887179
145,9884389
149,5228002
150,3952341
151,2633459
153,8424112
155,5413621
160,5453351

1.3. Коэффициент детерминации

Коэффициент детерминации используется для оценки качества подбора уравнения степенной регрессии.

Коэффициент детерминации характеризует долю дисперсии среднедневной заработной платы, руб. (у), объясняемую регрессией в общей дисперсии среднедневной заработной платы, руб. (у).

R^2

0,52915

Воспользуемся шкалой оценки силы связи между переменными в зависимости от . Так как , то сила связи между среднедушевым прожиточным минимумом в день одного трудоспособного, руб. () и среднедневной заработной платы, руб. (у) является заметной.

Значит уравнение регрессии объясняется 53% дисперсии среднедневной заработной платы, руб. (у) на долю прочих факторов, приходящихся на 47%.

1.4. Адекватность модели по F-критерию Фишера (α=0,05).

Оценка статистической значимости уравнения регрессии в целом осуществляется с помощью F-критерия Фишера, которая заключается в проверке гипотезы о статистической незначимости уравнения регрессии.

Fрассч

11,23821

1.5. Оценка точности модели.

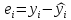
А – ошибка аппроксимации.

Аппроксимация

5,178802

Ошибка , что свидетельствует об удовлетворительной подборке модели к исходным данным.

1.6. Коэффициент эластичности.

Коэффициент эластичности показывает на сколько процентов в среднем по совокупности изменится среднедневная заработная плата, руб. (у) от своей средней величины при изменении среднедушевого прожиточного минимума в день одного трудоспособного, руб. ()

В общем случае:

Для степенной регрессии:

Э

0,538144

При изменении среднедушевого прожиточного минимума в день одного трудоспособного, руб. () на 1% среднедневная заработная плата, руб. (у) изменится на 0,538144%.

1.7. Построим точечный график по исходным данным.

2. Показательная модель

   1. Параметры уравнения показательной регрессии

y =

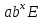
Необходимо линеаризовать модель (привести к линейному виду):

Произведем замену:

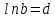
z=ln(y)
4,820282
4,976734
5,023881
4,890349
4,844187
4,927254
4,983607
5,068904
5,043425
5,030438
5,036953
5,123964

d	0,006378
c	4,41849

2.2. Показательная модель регрессии

Найдя параметры d и c, составим уравнение в линейном виде, выполнив его потенцирование, получим степенную модель.

yтеор
128,8415
133,0166
137,327
140,8756
142,6842
145,4407
149,199
150,1537
151,1144
154,0338
156,0112
162,0973

2.3. Коэффициент детерминации

Коэффициент детерминации используется для оценки качества подбора уравнения степенной регрессии.

Коэффициент детерминации характеризует долю дисперсии среднедневной заработной платы, руб. (у), объясняемую регрессией в общей дисперсии среднедневной заработной платы, руб. (у).

R^2

0,546678

Воспользуемся шкалой оценки силы связи между переменными в зависимости от . Так как , то сила связи между среднедушевым прожиточным минимумом в день одного трудоспособного, руб. () и среднедневной заработной платы, руб. (у) является заметной.

Значит уравнение регрессии объясняется 55% дисперсии среднедневной заработной платы, руб. (у) на долю прочих факторов, приходящихся на 45%.

2.4. Адекватность модели по F-критерию Фишера (α=0,05).

Оценка статистической значимости уравнения регрессии в целом осуществляется с помощью F-критерия Фишера, которая заключается в проверке гипотезы о статистической незначимости уравнения регрессии.

Fрассч

12,05936

2.5. Оценка точности модели.

А – ошибка аппроксимации.

аппроксимация

6,124207

Ошибка , что свидетельствует об удовлетворительной подборке модели к исходным данным.

2.6. Коэффициент эластичности.

Коэффициент эластичности показывает на сколько процентов в среднем по совокупности изменится среднедневная заработная плата, руб. (у) от своей средней величины при изменении среднедушевого прожиточного минимума в день одного трудоспособного, руб. ()

В общем случае:

Для показательной регрессии:

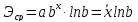
эластичность

0,562341

При изменении среднедушевого прожиточного минимума в день одного трудоспособного, руб. () на 1% среднедневная заработная плата, руб. (у) изменится на 0,562341%.

2.7. Построим точечный график по исходным данным.

3. Равносторонняя гипербола

3.1.Параметры уравнения показательной регрессии

Необходимо линеаризовать модель (привести к линейному виду):

Произведем замену:

Тогда:

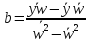
w=1/x
0,014493
0,013514
0,012658
0,012048
0,011765
0,011364
0,01087
0,010753
0,010638
0,010309
0,010101
0,009524

b	-6426,99
a	220,0962

2. Равносторонняя гипербола

Найдя параметры a и b, составим уравнение в линейном виде.

yтеор
126,9514
133,2449
138,7419
142,6625
144,4845
147,0622
150,2376
150,9887
151,7239
153,8385
155,1771
158,8867

3.3. Коэффициент детерминации

Коэффициент детерминации используется для оценки качества подбора уравнения степенной регрессии.

Коэффициент детерминации характеризует долю дисперсии среднедневной заработной платы, руб. (у), объясняемую регрессией в общей дисперсии среднедневной заработной платы, руб. (у).

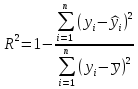
R^2

0,499468

Воспользуемся шкалой оценки силы связи между переменными в зависимости от . Так как , то сила связи между среднедушевым прожиточным минимумом в день одного трудоспособного, руб. () и среднедневной заработной платы, руб. (у) является заметной.

Значит уравнение регрессии объясняется 50% дисперсии среднедневной заработной платы, руб. (у) на долю прочих факторов, приходящихся на 50%.

3.4. Адекватность модели по F-критерию Фишера (α=0,05).

Оценка статистической значимости уравнения регрессии в целом осуществляется с помощью F-критерия Фишера, которая заключается в проверке гипотезы о статистической незначимости уравнения регрессии.

Fрассч

9,978747

3.5. Оценка точности модели.

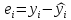
А – ошибка аппроксимации.

аппроксимация

6,360027

Ошибка , что свидетельствует об удовлетворительной подборке модели к исходным данным.

3.6. Коэффициент эластичности.

Коэффициент эластичности показывает на сколько процентов в среднем по совокупности изменится среднедневная заработная плата, руб. (у) от своей средней величины при изменении среднедушевого прожиточного минимума в день одного трудоспособного, руб. ()

В общем случае:

Для равносторонней гиперболы:

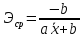
эластичность

0,495216

При изменении среднедушевого прожиточного минимума в день одного трудоспособного, руб. () на 1% среднедневная заработная плата, руб. (у) изменится на 0,495216%.

Вывод. Общая таблица.

	Fрассч	Апроксимация	R
линейная	11,63844	6,218619987	0,733389
степенная	11,23821	5,178801772	0,727427
показательная	12,05936	6,1242074	0,739377
равносторонняя гипербола	9,978747	6,360027106	0,706731

В равной степени хорошо нашу задачу описывает показательная модель регрессии, так как в ней максимален коэффициент детерминации и максимальна Fрассч.