Глава 6. Приведение матриц

6.1. Краткий обзор главы

• В предшествующих Главах обсуждалось использование ведущих степеней свободы (ВСС) в редуцированном анализе. Основная цель обращения к ведущим степеням свободы состоит в уменьшении размера матриц решаемых систем уравнений.

• В этой Главе более полно раскрывается сущность приведения матриц и даются руководящие принципы для выбора ведущих степеней свободы.

6.2. Что такое приведение матриц?

Приведение матриц - это способ уменьшить размер расчетной модели для сокращения времени счета и затрат ресурсов.

Процедура приведения связана с использованием в модели определенных ключевых степеней свободы, называемых ведущими степенями свободы.

Рассмотрим, например, трехэтажную рамную конструкцию, показанную на рис. 1 слева.

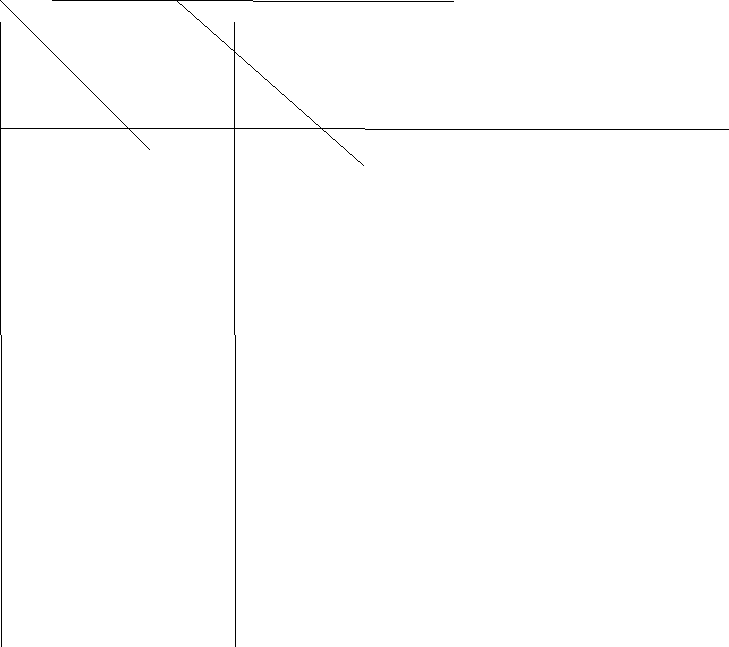
Рис.1

Расчетная модель этой рамы может быть разной в зависимости от того, нужна ли информация о напряжениях или о параметрах динамического отклика.

Если нужно получить распределение напряжений, то необходимо отобразить систему достаточно подробно. Так, для получения значений номинальных напряжений и деформаций потребуется балочная модель, показанная на рис.1 справа.

Если же интерес представляет динамический отклик рамы, то может оказаться приемлемой ее значительно более простая модель. Достаточно построить модель упрощенной геометрии, которая имеет такую же общую жесткость, массу и параметры демпфирования колебаний, как и исходная.

Показанной на рис. 2 модели достаточно для определения собственных частот и форм колебаний, для определения перемещений при динамическом переходном процессе или при воздействии гармонического нагружения.

Рис.2

Оба типа моделей имеют свои преимущества и недостатки: более подробная модель дает возможность получить более детальную картину напряжений и деформаций, но при более значительных затратах времени и вычислительных ресурсов, тогда как простая модель таких подробностей не дает, но позволяет быстрее получить результаты.

Обычно есть желание иметь подробные результаты при малых затратах. Так, например, при динамическом анализе переходного процесса предпочтение можно было бы отдать простой модели. Однако пиковые значения локальных напряжений может дать только подробная модель. Приведение матриц, или редуцированный анализ, делает возможным совмещение интересов.

Сначала рассматривается подробная модель (рис. 3), которая позволит получить информацию о перемещениях и локальных напряжениях.

Рис. 3

Затем с помощью процедуры, называемой редуцированием (приведением) способом Гуяня, программа ANSYS приводит исходную модель к более простой (с меньшим количеством степеней свободы), которая обладает эквивалентной жесткостью, приблизительно эквивалентной массой и характеристиками демпфирования.

Этапы приведения системы сохраняются (записываются) как часть процедуры Гуяня. Следует обратить внимание на то, что что метод приведения Гуяня не сводится к процедуре сосредоточения отдельных масс системы в более крупные массы.

Динамический анализ выполняется для простой, приведенной, модели (рис.4). Результаты анализа дают возможность обратить внимание на те шаги решения, для которых представляется интересным найти более подробную картину напряженного состояния.

Рис. 4

Выполняя в обратном порядке сохраненные шаги процедуры приведения, программа ANSYS в указанных шагах решения расширяет результаты, полученные для простой модели, на более детальную модель системы (рис. 5).

Рис. 5

Такая “расширенная” модель затем используется на стадии постпроцессорной обработки для получения подробных результатов.

Степени свободы, используемые для анализа простой модели, представляют собой подмножество всех степеней свободы подробной модели (рис. 6). Каждая из степеней свободы этого подмножества называется ведущей степенью свободы или просто мастер-степенью.

Рис. 6

Ведущие степени свободы могут быть заданы пользователем явно, выбраны автоматически программой или получены комбинированием двух этих способов. Удаляемые из матрицы степени свободы, называются подчиненными степенями.

Если обозначить общее число степеней свободы через n, число ведущих степеней - через m, а число подчиненных - через s, то справедливо равенство

m + s = n .

Для того чтобы приведение системы было выгодным, должно выполняться условие

m n.

Идея редуцирования, приведения, матриц заключается в предположении, что на низших частотах можно пренебречь инерционными силами, обусловленными массами с подчиненными степенями свободы, по сравнению с упругими силами ведущих степеней. Таким образом, общая масса системы может быть перераспределена между ее мастер-степенями на основе сопоставления относительных жесткостей системы, относящихся к подчиненным и ведущим степеням. Поэтому с подчиненными степенями свободы не связаны ни массы, ни силы сопротивления, и на их перемещения влияет только матрица жесткости системы.

Это сводит проблему к формированию матрицы, которая с помощью коэффициентов жесткости связывает перемещения подчиненных и ведущих степеней. Следовательно, если определить перемещения для ведущих степеней свободы, то могут быть вычислены и перемещения для подчиненных. Как только становятся известными перемещения для всех степеней свободы системы, могут быть определены напряжения и деформации.

Итак, полная процедура получения решения может быть разбита на три существенно разных шага:

шаг 1 - перераспределение общей массы системы по мастер-степеням свободы и получение “приведенных” матриц [K], [M] и [C] для системы с ведущими степенями свободы;

шаг 2 - использование редуцированных матриц в разрешающих уравнениях и получение перемещений для ведущих степеней свободы;

шаг 3 - расширение решения на полный набор степеней свободы, расчет напряжений и деформаций.