3.6.6. Приложение нагрузок и получение решения
С использованием команды LSSOLVE выполняется решение для всех шагов нагружения. Альтернатива процедурам LSWRITE - LSSOLVE заключается в использование множества команд SOLVE.
Выходные данные состоят, главным образом, из файла результатов, т.е. файла с именем Jobname. RST.
3.6.7. Диаграмма потока данных
3.6.8. Просмотр результатов (постпроцессорная обработка)
Бинарный файл Jobname.RST, содержащий результаты анализа, является файлом данных, который используется постпроцессорами программы ANSYS: POST1 и POST26.
POST1 Постпроцессор общего назначения
Используется для выбора, сортировки, печати и вывода на экран выходных данных (перемещений, напряжений и т.д.) в любой момент времени переходного процесса.
POST26 Постпроцессор истории нагружения
Выходные данные могут быть записаны как переменные.
Записанные данные могут быть представлены графически в виде зависимости от времени или других переменных.
Разрешены арифметические операции.
Записанные переменные можно дифференцировать или интегрировать.
Некоторые полезные команды постпроцессора POST26:
NSOL Задает узловые перемещения, которые будут сохранены:
NSOL, NVAR, NODE, Item, Comp, Name
NVAR - произвольное число ( 2), присваиваемое переменной;
NODE - узлы, для которых сохраняются данные;
Item - тип данных: U (смещения), ROT (повороты);
Comp - компоненты: в направлении X, Y или Z;
Name - имя переменной (до 8 символов) для вывода на печать или экран дисплея.
PRVAR Задает переменные, выводимые на печать:
PRVAR, NVAR1, NVAR2, ..., NVAR6
NVAR1 - ссылочный номер переменной (до 6 в одной строке).
PLVAR Задает переменные для вывода на плоттер (как функции вре-мени, по умолчанию):
PLVAR, NVAR1, NVAR2, ..., NVAR10
NVAR2 - ссылочный номер переменной для вывода на плоттер (до 10 переменных на один график).
3.6.9. Пример
Дано: груз массой 50/g фунтов падает с высоты 6 футов на покрытый липким веществом подпружиненный поддон массой 25/g фунтов, как показано на рисунке. После падения груза отскока груза не происходит. Жесткость пружины равна 100 фунт/дюйм.
Цель расчета: определить максимальное отклонение h поддона.
|
М1 |
|
вес |
масса |
|
72 д |
|
(ф) |
(ф-с2 / д) |
|
|
М1 |
50 |
50/г |
|
М2 |
М2 |
25 |
25/г |
|
К
|
|
k = g = |
100 ф/д 386 д/с2 |
Теоретическое решение:
h = (статическое и динамическое отклонения) = 0.25 + 7.45 = 7.70 дюйм.
Для решения задачи используется комбинированый элемент COMBIN40. Используются два элемента - один в качестве зазора и массы M1, другой - в виде пружины и массы M2. Жесткость закрытого зазора принимается равной 10000 фунт/дюйм, т.е. на два порядка больше, чем жесткость пружины. Итак, kgap=10000 фунт/дюйм.
Частота замыканий зазора (при условии, что масса M2 не движется) определяет значение шага интегрирования по времени ITS:
fgap = 1/2(kgap / M1) = 44.24 Гц,
следовательно, ITS = 1/30 fgap 0.0008с.
Контакт груза с поддоном происходит через 0.61 с, так как время падения груза с высоты 72 дюйма 0 = (2.72/g)1/2 0.61 с. Время решения принимается равным 0.72 с, чтобы число итераций составило 900.
Используются два шага нагружения. На первом шаге нагружения блок весом 50 фунтов удерживается на месте, и рассматривается статическое смещение пружины под действием массы поддона. На втором шаге нагружения задается интервал времени 0.72 с, а груз освобождается.
Ввод задается следующим образом.
ПОСТРОЕНИЕ МОДЕЛИ
/PREP7
/TITLE,элементы зазора и оптимизация шага по времени, trn–f-1
ET, 1, COMBIN40, 1, , 2, , , 2 ! Зазор закрыт, степень свободы UY, масса в узле j
ЗАДАНИЕ УЗЛОВ (ИЗ-ЗА ОСОБЕННОСТЕЙ ЭЛЕМЕНТА COMBIN40)
N, 1, , – 10
N, 2
N, 3, , 72
G = 386.4 ! Гравитацинная постоянная
! * * * * * * * * * Задание груза и зазора под грузом
R, 1, 10000, , (50/G), 72 ! Жесткость зазора, масса груза, величина зазора
REAL, 1
E, 2, 3
ЗАДАНИЕ ПОДДОНА ИПРУЖИНЫ
R, 2, 100, , (25/G) ! Жесткость пружины, масса поддона
REAL, 2
E, 1, 2
FINISH
ПРИЛОЖЕНИЕ НАГРУЗОК И ПОЛУЧЕНИЕ РЕШЕНИЯ
/SOLU
ANTYPE, TRANS ! Нелинейный анализ переходных процессов
KBC, 1 ! Ступенчатое изменение граничных условий
ACEL, , G ! Ускорение силы тяжести
D, 1, UY ! Закрепление узла 1 в направлении UY
Перед началом расчета узел 2 должен перейти в состояние статического равновесия.
D, 3, UY ! Закрепление узла 3 в направлении UY для шага 1
TIMINT, OFF ! Выполняется статический анализ
TIME, .000001 ! Фиктивный интервал времени
NSUBST, 2 Два промежуточных шага для задания нулевой начальной скорости
LSWRITE ! Запись шага нагружения 1
TIMINT, ON ! Выполняется динамический анализ
TIME, 0.72 ! Время до окончания шага нагружения 2
NSUBST, 900 ! Число итераций 900 (= .72 / 0.0008)
OUTRES, , 1
AUTOTS, ON ! Оптимизация шага интегрирования
DDELE, 3, UY ! Освобождение узла 3 в направлении UY
LSWRITE ! Запись шага нагружения 2
LSSOLVE, 1, 2
FINISH
ПРОСМОТР РЕЗУЛЬТАТОВ
/POST26
NSOL, 2, 2, U, Y ! Переменная 2 - это перемещение UY в узле 2
NSOL, 3, 3, U, Y ! Переменная 3 - это перемещение UY в узле 3
SOLU, 4, DTIME ! Переменная 4 - шаг интегрирования по времени
/GRID, 1
/TITLE, ПРИМЕР - ПЕРЕМЕЩЕНИЕ ПОДДОНА ВЕСОМ 25 ФУНТОВ trn-f-1
/AXLAB, Y, DISP ! Метка оси Y
PLVAR, 2 ! График переменной 2
/TITLE, ПРИМЕР - ПЕРЕМЕЩЕНИЕ ГРУЗА ВЕСОМ 50 ФУНТОВ trn-f-1
PLVAR,3
/TITLE, ПРИМЕР - ШАГ ИНТЕГРИРОВАНИЯ ПО ВРЕМЕНИ trn-f-1
/AXLAB, Y, SEC
PLVAR, 4
FINISH
По программе ANSYS получено решение для максимального перемещения поддона h = 8.00 дюймов. Ниже приведены графики перемещений.
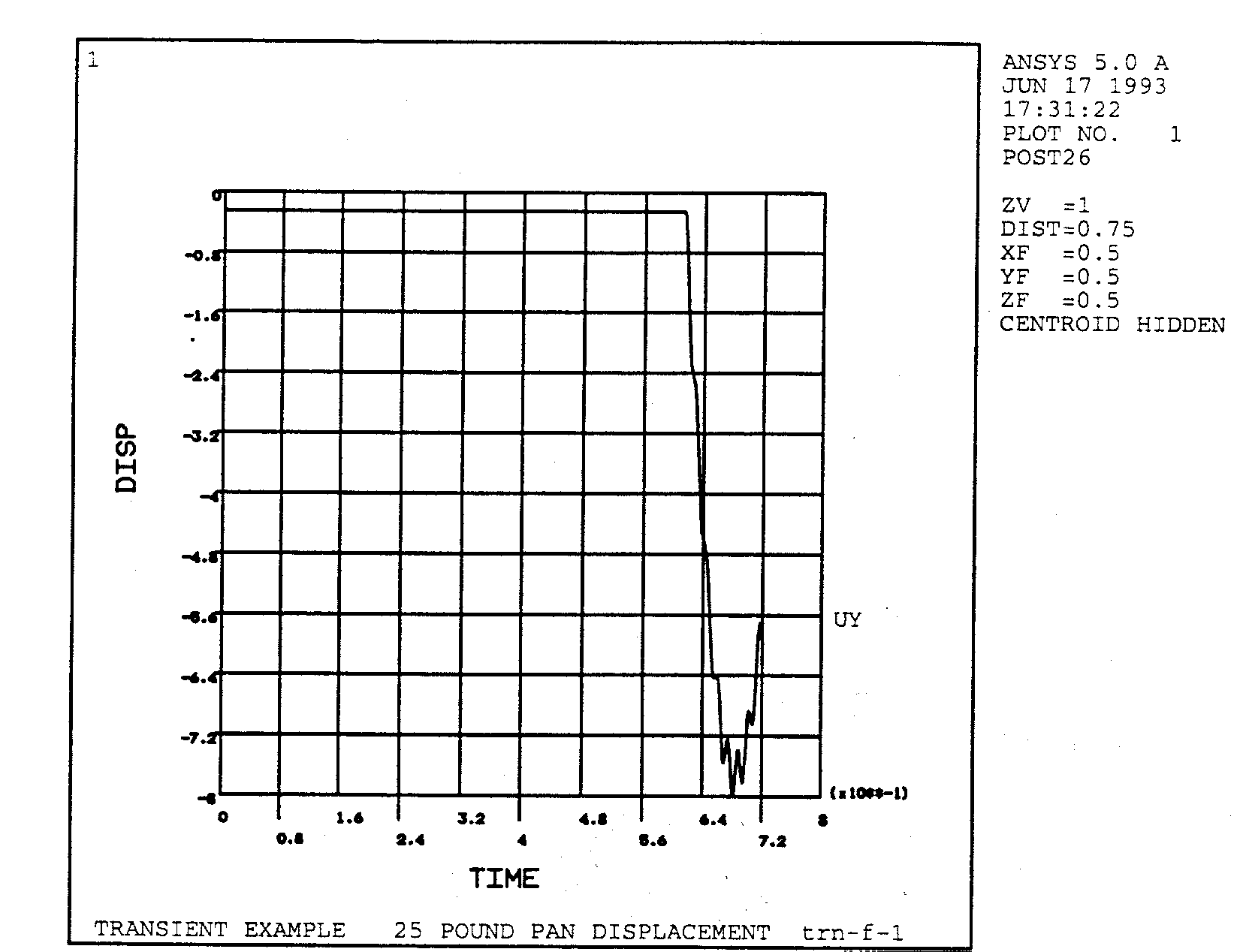
Теоретическое решение предполагает полностью неупругое соударение, т.е. считается, что вся энергия передается поддону. Однако решение по программе ANSYS более реалистично. Хорошо отражено совместное колебание обеих масс, (см. графики зависимости “перемещение-время”). Можно видеть проявление колебаний одной массы относительно другой. Следует обратить внимание на то, что можно было проследить отскок после удара, отказавшись от опции блокировки зазора.
На графике изменения шага по времени показано, как меняется шаг интегрирования от итерации к итерации. Видно, что параметр ITS увеличивается во время свободного падения и уменьшается до минимального, заданного, значения ITS непосредственно перед закрытием зазора.
ANSYS 5.0 A
ИЮНЬ 17 1993
17:31:23
РИС.№3
POST26
ZV = 1
DIST = 0.75
XF = 0.5
YF = 0.5
ZF = 0.5
CENTROID HIDDEN
пример анализа переходных процессов, размер приращения времени