4.5.4.1. Диаграмма потока данных (стадия расширения)

4.5.5. Обзор результатов двух стадий решения

• Обычно выполняется в постпроцессоре POST1 для получения:

• уровней равных напряжений;

• графиков деформированного состояния;

• распечаток результатов в табличной форме; и т.д.

• Постпроцессор POST26 можно использовать для получения:

• графиков “перемещение-частота”;

• графиков “напряжение-частота”;

• графиков “деформация-частота”;

• арифметические операции с комплексными числами; и т.д.

4.6. Пример расчета

Дано: одномассовая система с демпфером под действием гармонической силы с амплитудой 50 фунтов. Коэффициент демпфирования = 10 %.

Цель расчета: определить отклик системы в диапазоне частот 0 - 4 Гц. Найти амплитуду колебаний при резонансе.

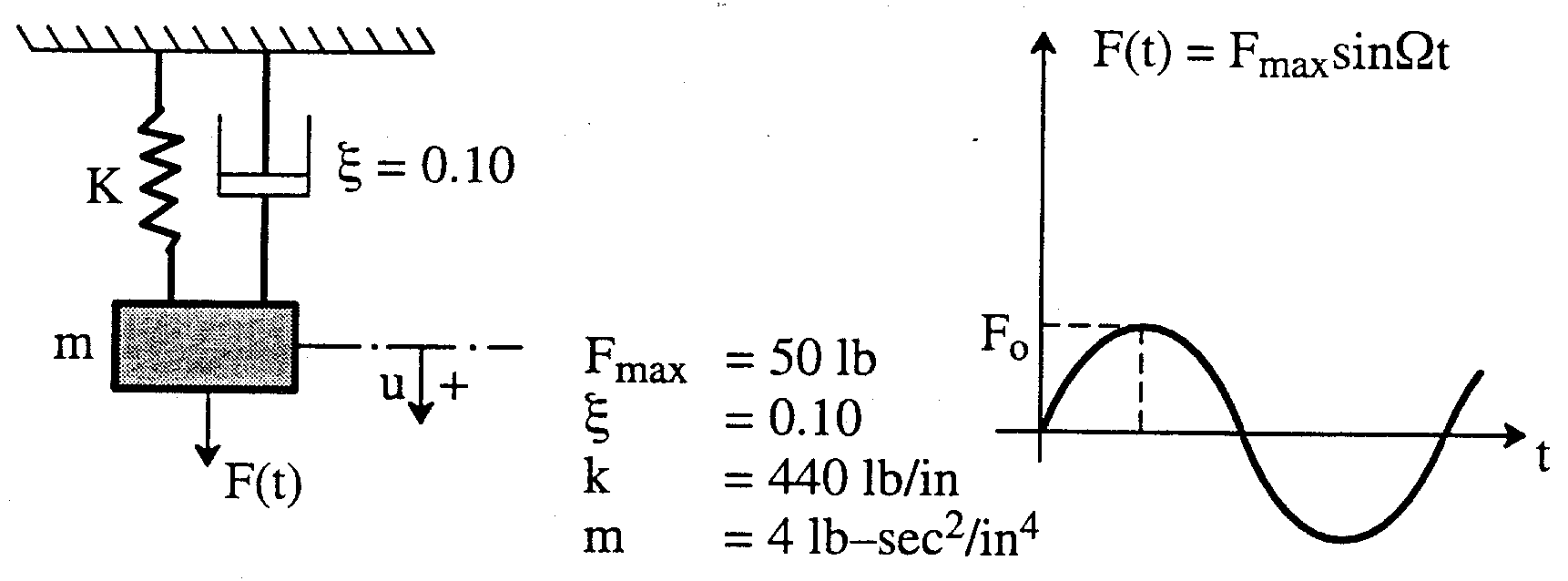
Теоретическое решение:

Резонансная частота f _n = 1/2 (k / m) = 1.6692 Гц.

Резонансная амплитуда**, u_res = (F_max / k) / 2 (1- ²)= 0.5710 д.

Используемый подход:

Для получения решения при резонансной частоте заданный диапазон частот разбивается на два шага нагружения:

шаг нагружения 1: 0.0 . . . 1.6692 Гц;

шаг нагружения 2: 1.6692 . . . 4.0 Гц.

Последовательность команд при использовании программы ANSYS будет следующим:

ПОСТРОЕНИЕ МОДЕЛИ

/PREP7

/TITLE, пример гармонического анализа hr-r-1

ET, 1, COMBIN40, , , 2, , , 2 ! Степень свободы UY, вся масса в узле J

R, 1, 440, , 4 ! Жесткость, масса: k = 440, m = 4

N, 1

N, 2

E, 1, 2

FINISH

ПРИЛОЖЕНИЕ НАГРУЗОК И ПОЛУЧЕНИЕ РЕДУЦИРОВАННОГО РЕШЕНИЯ (СТАДИЯ ПЕРЕМЕЩЕНИЯ)

/SQLU

ANTYPE, HARMIC ! Отклик на гармоническое воздействие

HROPT, REDUC ! Редуцированный метод решения

HROUT, OFF ! Результаты в виде амплитуды и фазового угла

M, 2, UY ! Перемещение UY в узле 2 - ведущая степень

D, 1, UY

F, 2, FY, 50

HARFRQ, , 1.6692 ! Интервал частот [0, 1.6692] Гц, шаг 0.16692,

NSUBST, 10 ! так как число шагов решения равно 10

KBC, 1 ! Скачкообразное приложение граничных условий

DMPRAT, 0.1 ! Коэффициент демпфирования

OUTPR, , 10 Вывод на печать каждого 10-го дополн. шага

! Сохранение данных командой OUTRES не используется

LSWRITE ! Запись данных о шаге нагружения 1

HARFRQ, 1.6692, 4 ! Интервал частот [1.6692, 4] Гц, шаг 0.15538

NSUBST, 15

OUTPR, , 15

LSWRITE ! Запись данных о шаге нагружения 2

LSSOLVE, 1, 2

FINISH

ОБЗОР РЕЗУЛЬТАТОВ

/POST26

FILE, , rfrg ! Файл перемещений

NSOL, 2, 2, U, Y

PRCPLX, 1 ! Вывод результатов (амплитуда, фазовый угол)

PRVAR, 2

/GRID, 1

PLVAR, 2

FINISH

Результаты решения при резонансе: u_res = 0.5682 l д. (ошибка = 0.49 %).

Ниже приведен график зависимости амплитуды от частоты.

4.6.1. Задача для самостоятельного решения:

прессовая машина, установленная в центре стола, испытывает действие гармонически меняющейся силы с амплитудой 150 фунтов. Частота силы находится в диапазоне 12 . . . 90 Гц. Определить реакцию стола.

Дано: стол тот же самый, как и прежде, но толщина столешницы равна 0.25 д.

Порядок решения: на основе готового входного файла для задания узлов, элементов, реальных констант и свойств материала выполнить следующее:

1. задать толщину столешницы равной 0.25 дюйма;

1. выполнить модальный анализ для определения первых 6-ти собственных частот и форм колебаний, в постпроцессоре POST1 получить графики мод колебаний;

1. сменить вид анализа и опции решения для расчета отклика на гармоническое воздействие;

1. задать коэффициент демпфирования 3 %;

1. выполнить редуцированный анализ;

1. с помощью постпроцессора POST26 получить график смещения узла в центре стола;

1. выполнить расширение решения для критических значений частоты и угла фазы;

с помощью постпроцессора POST1 получить распределение эквивалентных (по Мизесу) напряжений в столешнице стола.

_____________________________________________________________________________

Harmonic Response Analysis

11