Дискретная математика

Читал: Павлов Игорь Сергеевич

Набрал: Смирнов Вадим Евгеньевич

ННГУ, 2000 г.

Глава I. Теория множеств.

Лекция 1.

Понятие множества

Определение.Множество– объединение в единое целое объектов, хорошо различаемых нашей интуицией или мыслью. Объекты, составляющие множество, называютсяэлементами множества. Множества обозначаются большими латинскими буквами (S), элементы множеств – маленькими (x,y).

Обозначения: Элемент принадлежит множеству:xS

Элемент не принадлежит множеству: yS

Примеры множеств:N- множество натуральных чисел,Z- множество целых чисел,Q- множество рациональных чисел,R- множество действительных чисел,C- множество комплексных чисел.

Определение. Множество называетсяконечным, если оно содержит конечное число элементов.

Определение.Пустое() множество не содержит элементов.

Способы задания множеств:

1. Задание полного спискаэлементов.H= {понедельник, вторник, … воскресенье}

2. Указание некоторого характерного свойства.H= {x| свойство}H= {x|x= 2n,nN}

(иногда известны не все элементы множества)

Отношения между множествами:

Определение. Два множества называютсяравными, если они состоят из одних и тех же элементов.

(А = В)  (x  A, x  B ^ x  B x  A)

Пример.A– множество положительных четных чисел.B– множество натуральных чисел, состоящих из сумм двух положительных нечетных чисел.

Доказательство:Необходимость. Пусть хАx = 2n = (2n - 1) + 1xB

Достаточность.xBx= 2p– 1 + 2q– 1 = 2(p+q– 1)хА

Следовательно: А = В.

Примеры: {2, 4, 6} = {6, 2, 4} = {4, 4, 2, 6}

Элементами множества могут быть и сами множества:

{студенты на лекции} = {421, 422, …, 426}

{1, 2}  {{1, 2}}

Отношение включения.

Определение. Если каждый элемент множества А является элементом множества В, то А В (включено), при этом А – подмножество В. Если АВ ^ АВ, то АВ (строго включено).

Основные свойства Отношения включения:

1. А А

2. (А В ^ ВС)АС

3. (А В ^ ВА)А = В

Доказательство 2-го свойства:х  АхВх  ССледовательно: АС.

Примеры: АВ ^ ВСАС АВ ^ ВСАС

Сравнимость множеств.

Определение. Множества А и Всравнимые, если АВВА

Пример.A= {x|x> 3},B= {x|x1},C= {x| -5 <x≤ 2}

ABА и В сравнимы, А и С не сравнимые, В и С не сравнимые.

Диаграмма Венна.

Определение.U–универсальное множестводля данной задачи, если все рассматриваемые в этой задаче множества являются его подмножествами.

Определение.Диаграммой Веннаназывается схема множестваUв виде прямоугольника, а других множеств в виде кругов или в какой-то другой области.

Алгебраические операции над множествами.

Определение.Относительным дополнением множества А до множества Х называется Х\А = {x|xX^xA} (разность Х - А, Х без А).

Определение.Абсолютным дополнениеммножества А называется множество всех тех элементов, которые не принадлежат А.=U\A– абсолютное добавление.

Определение.Объединением множеств(АВ) называется множество, элементы которого принадлежат хотя бы одному из этих множеств.

Определение.Пересечением множеств(АВ) называется множество, элементы которого принадлежат каждому из этих множеств.

Определение.Симметрической разностью множествназывается множество, элементы которого принадлежат ровно одному из этих множеств: АВ=(А \ В)(В \ А).

Законы алгебры множеств.

1. Коммутативность

   1. А В = ВА

   2. А В = ВА

   3. А В = ВА

   4. А \ В В \ А

2. Ассоциативность

   1. А (ВС) = (АВ)С

   2. А (ВС) = (АВ)С

   3. А (ВС) = (АВ)С

   4. А \ (В \ С) (А \ В) \ С

3. Дистрибутивность

   1. А (ВС) = (АВ)(АС)

   2. А (ВС) = (АВ)(АС)

4. – без названия

   1. А А = А

   2. А А = А

   3. А  = 

   4. А = А

   5. А U= А

   6. А U=U

5. Законы де Моргана

   1. =

   2. =

6. Дополнение к Uи

   1. =

   2. =U

7. Поглощение

   1. А (АВ) = А

   2. А (АВ) = А

8. – без названия –

   1. Если А, АВ = А, то В =

   2. Если А, АВ = А, то В =U

9. Если А В =U^ АВ ==> В =А =

10. Двойное дополнение: = А

Полезные тождества:

1. А В = АВ(АВ)

2. А \ В = А (АВ)

3. А В = (АВ)АВ

4. А \ В = (А В)В

5. А В = А \ (А \ В)

6. А В = (АВ)(А \ (А \ В))

Нельзя выразить \ через «» и «»,или «» через «» и «\»

Лекция 2.

Определение. Равенство алгебры множеств, полученное заменой всех знаковна,на, Uна,на Uназываетсядвойственным.

Все рассматриваемые законы алгебры множеств двойственны.

Закон 9 – самодвойственный.

Для разности двойственный закон верен, т.к. А \В = А

Закон дистрибьютивности определения относительно пересечения:

А (ВС) = (АВ)(АС)

Доказательство:

а) Необходимость: x  (A  (B  C))  (x  A  x  B  C);

x ( B ( C  (x  B) ^ (x  C)  (x  A  B) ^ (x  A  C)  x  (A  B)  (A  C)

б) Достаточность: x  (A  B)  (A  C)  (x  A  B) ^ (x  A  C) 

 ((x  A)  (x  B) ^ (x  A)  (x  C)) (x  A)  ((x  B) ^ (x  C))  x  А(ВС)

Закон де Моргана:=

Доказательство:

а) Необходимость:x x  (A  B)  (x  A) ^ (x  B)  (x  ) ^ (x  )  x  ()

б) Достаточность: x  ()  (x  ) ^ (x  )  (x  A) ^ (x  B)  x  (A  B)  x 

Примеры:

 A \ B =  | A \ B = A  =   A  B 

 B \ A =  |  B \ A = B  =   B  A   A = B



A  B =   A = B

Утверждение. Отношения включения множеств могут быть определены в терминахи.

Следующие утверждения о произвольных множествах А и В попарно-эквивалентны:

1. АВ = А

2. А В = ВA  B

3. А \В =

4. А В =U

5. А В =

Примеры:

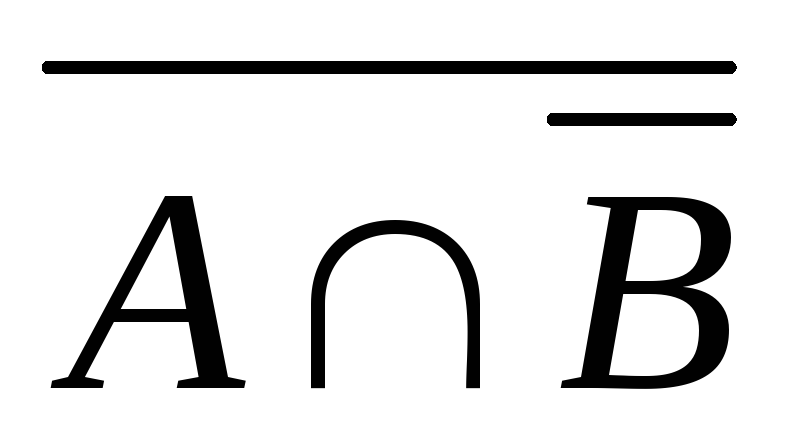1. B = (  ) B = (  B)  B =  (B  B) =  B

2. (A \ B)  (A  B) = (A  )  (A  B) = A  ( B) = A  U = A

Обобщенные тождества алгебры множеств:

1. Обобщенная дистрибьютивность

а) A  (B­₁  B₂  ...  B_n) = (A  B₁)  (A  B₂)  ...  (A  B_n)

а) A  () =(1)

б) A  () =

Доказательство утверждения (а): (методом математической индукции)

1) n = 2: левая часть (1) =A  (B­₁  B₂)

правая часть (1) = (A  B₁)  (A  B₂)левая часть = правая часть (по доказанному ранее)

2) Допустим A  () =, (k  N, k  2)- верно

Надо доказать: A  () =

Доказательство: A  ()=A  (B_k+1) = [по доказательству в 1] =

= (A  ()) (A B_k+1) = [по допущению] =  (A  B_k+1) =

Так как выполнено оба условия обобщенного принципа математической индукции, то равенство (1) верно.

2. Обобщенный закон де Морга

а) =  ... 

б) =

Доказательство утверждения (а): (методом математической индукции)

1) n = 2: левая часть =

правая часть = левая часть = правая часть (по доказанному ранее)

2) Допустим: =, (k  N, k  2)– верно. Надо доказать:=.

Доказательство: = = [по доказательству в 1] =

== [по допущению] ==.

Так как выполнено оба условия обобщенного принципа математической индукции, то равенство (1) верно.