4.4.1Одномерное течение сжимаемого газа по трубам конечной толщины.

Пусть характерный масштаб изменения всех полей и диаметра трубы в продольном направлении равен L_, а харaктерный поперечный масштаб трубы - L_ (это будет и поперечный масштаб всех полей). Пусть L_ >> L_ . Из уравнения сохранения массы для стационарного течения следует,что,

;

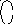
Из этого уравнения нетрудно получить оценку

, т.е. .

Запишем уравнение Эйлера для стационарного течения

.

Пусть. Проекция уравнения на продольное направление:

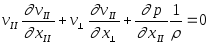.(4.32)

На поперечное направление

. (4.33)

Покажем, что существует такое решение, которое можно представить в виде

p = p( x_||) + p₁( x_|| , x_), где p₁ << p.

Подставим p в уравнение (4.32), получим оценку:

, которая с учетом уравнения непрерывности , примет вид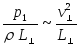, т.е..

Подставим в уравнение оценочное значение давления (4.32)

, т.е. , посколькуv_ << v_ , то p₁ << p, . Значит, с точностью до малых величинможно считать, что р зависит только от продольной координаты х. Но если р зависит только от х, т.е. сила зависит только от х, то можно считать, что v_|| зависит только от х, с точностью до малых ~(L / L_||)². Во всяком случае такое решение существует. Получается, что по сечению трубки v постоянно, р — постоянно. Значит из закона сохранения массы следует, что и  постоянно. Т.е. мы получаем, что для трубки конечной толщины применимо уравнение сохранения потока массы, полученное для тонкой трубки:

d / dx (  v S ) = 0 (4.33)

а также на любой линии тока (а они все одинаковы) справедливо соотношение , вытекающее из закона Бернулли и закона сохранения энергии для одномерного движения

(4.34)

(4.35)

Чтобы система была замкнута, необходимо включить сюда еще уравнение состояния в виде, соответствующем , например, двухпараметрическим средам, которым относится идеальная жидкость или газ:

u = u ( p,  )

Задача об истечени газа из сосуда

Рассмотрим задачу об истечении газа из сосуда, в котором поддерживается давление р₀, а плотность газа ₀. Истечение газа происходит по трубке (соплу) переменного сечения S(х). Пусть S(х) монотонно убывает. Задача состоит в том, чтобы найти скорость истечения газа из трубки и распределение параметров газа (давления, плотности, скорости) по ее длине.

Выберем линию тока, проходящую из глубины сосуда, где р = р₀ , v = 0 через сопло. Применим систему уравнений для течения жидкости вдоль линии тока. Поскольку внешние массовые силы и источники тепла отсутствуют( = 0, q = 0), то законы течения газа по тонкой трубке примут вид:

Сохранение потока импульса

Сохранение потока энергии

Считаем, газ совершенный, тогда уравнение состояния

(436)

Эти уравнения справедливы на линии тока.

Начиная с некоторого х на выбранной линии тока, которая находится внутри трубки, течение газа можно считать одномерным и добавить закон сохранения потока массы в виде

d / dx (vS (x)) = 0 (4.37)

Чтобы решить задачу, надо совместно решать систему (4.34-4.37). Исключая из уравнений (4.34) и (435) v², с учетом уравнения состояния мы получим уравнение адиабаты для совершенного газа. При постоянной удельной теплоемкости c_v = const имеем:

Отсюда , где.

Получили уравнение адиабаты.

Подставляем полученную связь в (4.34) или в (4.36), получим связь скорости с давлением

Интегрирование дает

Константу находим из условия, что в глубине сосуда на линии тока p = p₀,  = ₀, v = 0 т.е.

(4.38(а))

Подставляя сюда  как функцию р, получим зависимость скорости течения газа от давления

(4.38)

Заметим, что в силу стационарности течения p₀, ₀ в (4.37)и в уравнении адиабаты одни и те же. Чтобы получить значение скорости на выходе из сопла , приравняем значение р в (4.37), равным р = р_e , а при произвольном р_e < р < р₀ получим значения скорости вдоль трубки. Казалось бы, задача почти решена. Надо найти только распределение всех величин по трубке при заданной зависимости S(х) — зависимости сечения сопла от х. Для этого проинтегрируем уравнение (4.37), так что

 v S ( x ) = Q (4.39)

,где Q-определяется граничными усорвиями, S(х) — заданная убывающая функция по условию задачи, — растущая функция. Найдем зависимостьv от р; v определяется из (4.38);  = ₀ (p / p₀)^1/ — уравнением адиабаты. Тогда

(4.40)

Построим график функции v(р)/ ₀v₀ ,где

Рис.

Обсудим возможность реализации этой зависимости. Давление вдоль трубки должно монотонно падает от р₀ до р_e

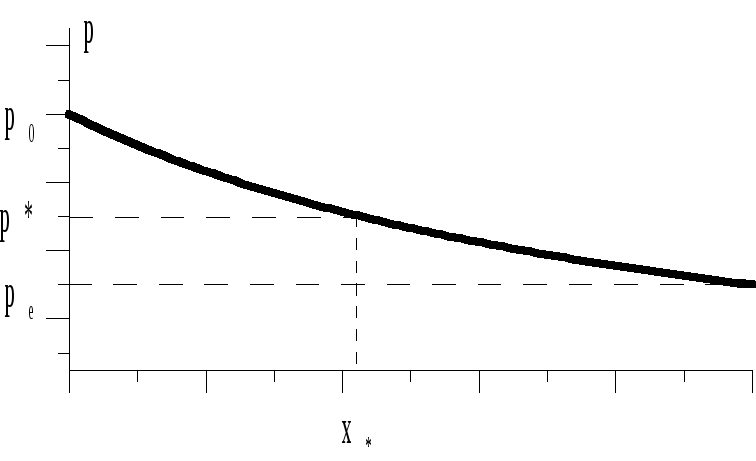
Рис.

Но тогда  v ( x ) имеет немонотонный характер:

Рис.

Значит, при монотонной зависимости S(x) условие  v S ( x ) = Q = const. не может быть выполнено, если p_e < р^*, где р^* — точка максимума функции  v(p). Это давление называется критическим.

Определим эту точку максимума:

d / dp [ v(p)] = 0

Обозначим y = p / p₀

Тогда надо найти максимум функции:

(4.41),

где f(y) = y^2/ (1 – y^{(–1)/}),

Отсюда для координаты имеем , при этом давление и плотность равны:,(4.42)

.

Скорость потока в точке максимума v найдем из уравнения Бернулли:

(4.43)

Подставляя p_* и _*, из (4.42)получим:

(4.44)

Заметим, что при р = р_* ,  ₌ _* скорость звука принимает значение:

(4.45)

т.е. в критической точке скорость потока равна скорости звука.

Заметим, что параметры потока в критической точке р_* , _*, c_* однозначно связаны с параметрами газа на линии тока в точке, где газ покоится: р₀ , ₀, c₀ — параметры торможения. Действительно,

(4.46)

Итак, соблюдение условия vS(x)=const возможно при монотонной зависимости S(x), только если давление на выходе трубки p_e  p_* (критическое давление). Когда p_e = p^*, то скорость газа в выходном сечении равна скорости звука c_*. Т.е. ,если мы снижаем выходное давление от значения p₀ до p_*, то скорость газа в выходном сечении трубки монотонно растет от 0 до c_*. Что будет, если мы теперь будем дальше понижать давление на выходе из трубки? Будем рассуждать. Газ выходит из трубки со скоростью звука. Уменьшим давление, т.е. создадим возмущение давления. Чтобы газ внутри трубки “узнал”, что давление снаружи понизилось, необходимо, чтобы возмущения давления распространились вверх по потоку. Но они распространяются со скоростью звука c^*, т.е. возмущения не смогут подняться вверх по потоку, и газ “не узнает”, что давление снаружи изменилось. На выходе внутри трубки давление так и останется p^*, а скорость v = c^*, а плотность ^*. Таким образом, зависимость плотности потока газа от давления вне сосуда p_e будет выглядеть следующим образом:

Рис.