7.Простые волны

При рассмотрении малых возмущений идеального газа мы показали, что возмущения всех гидродинамических величин удовлетворяют волновому уравнению, например, для возмущения скорости имеем так называемое волновое уравнение:

(7.1)

Решением этого уравнения являются так называемые бегущие волны:

,

где - произвольные функции

Пусть имеется решение в виде одной бегущей волны u1 = f1 ( x - c0 t ). Но тогда все гидродинамические величины также должны быть функциями ( x - c0 t ), а это, в свою очередь, значит, что все гидродинамические величины являются функциями друг друга, т.е. 1 =  ( u1 ); p1 = p1( u1 ) и т.д. Если мы будем рассматривать возмущения конечной амплитуды, то они не будут удовлетворять такому простому уравнению(7.1), но можно попробовать поискать решение одномерных уравнений гидродинамики, удовлетворяющие условию, что все величины могут быть выражены в виде функций друг друга, т.е.  =  ( u ); p = p( u ) и т.д.

Система уравнений динамики жидкости для одномерных течений имеют вид:

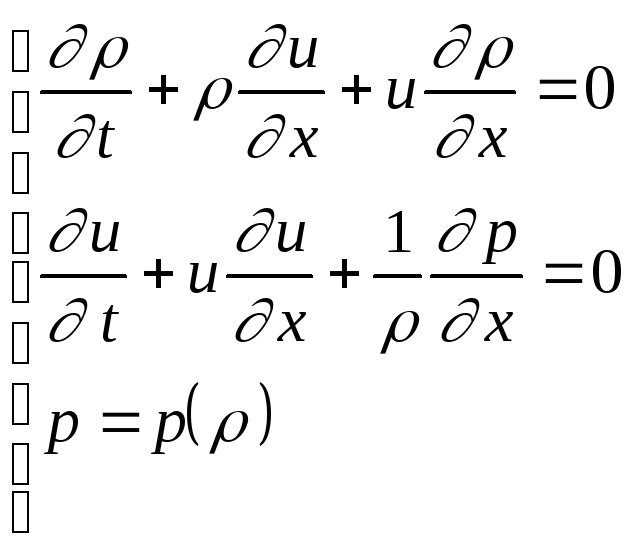(7.2)

Пусть все величины являются функциями скорости u. Тогда система примет вид:

(7.3)

Эта система совместна, если детерминант:

т.е. (7.34

- это уравнение для- . Оно дает возможность связать различные величины в волне. Кроме

того, оно входит в уравнение для u.

.(7.5)

.

Или, подставляя (7.4) в (7.5), получим:

(7.6)

Поскольку все гидродинамические величины являются функциями друг друга, то уравнение (7.6)имеет вид:

(7.7)

где - местная скорость звука, которая является функцией u.

Эту функцию можно легко найти.Действительно, из (7.3) следует, что:

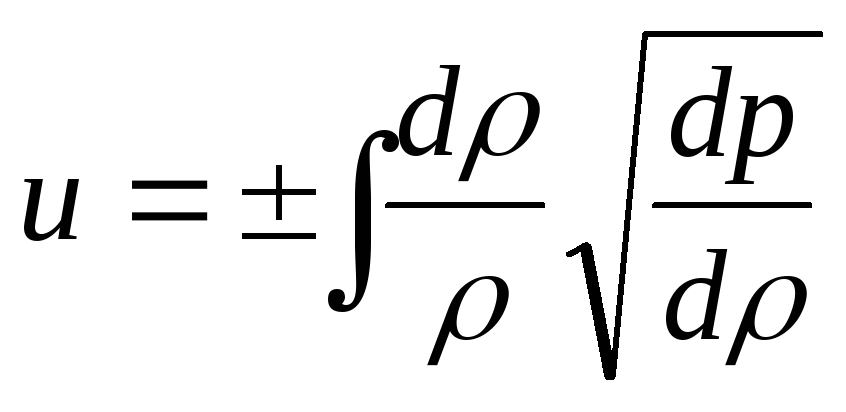(7.4)

Отсюда можно найти u = u (  ), p = (  ) , а , следовательно, c ( u )

Проделаем эту процедуру для идеального газа с постоянной теплоемкостью для к оторого p = A, где А – некоторая константа. Тогда из (7.4) имеем:

.(7.5)

Константу можно найти из условия отсутствия возмущений при . Тогда из (7.5) имеем:

(7.8)

При этом скорость звука равна

(7.7)

Сравнивая эти две формулы, легко видеть, что

(7.9)

Итак, уравнение для u в идеальном газе принимает вид:

(7.10)

Найдем теперь решение уравнения для u.

(7.11)

Заметим, что поскольку u = u( x, t ), нетрудно найти скорость, с которой перемещается u=const/ Действительно,

(7.12)

Сравнивая эти два уравнения, легко видеть, что

(7.13)

Это уравнение характеристик для u. На характеристиках(7.13) значения u сохраняются. Это значит, что решение можно легко записать

x = x₀ ( u ) + ( u  cu ) t (7.14)

x₀ ( u ) определяется начальными и граничными условиями.

Полученное решение (7.14) называется простой волной. Это точное решение одномерных уравнений идеальной гидродинамики. Оно описывает изэнтропическое течение газа без потерь. Поскольку все величины являются функциями друг друга, то все гидродинамические величины сохраняются на характеристиках.

Рассмотрим качественно, как ведет себя решение (7.14). Рассмотрим волну, бегущую вправо:

Для идеального газа уравнение простой волны имеет вид:

(7.15)

 - растущая функция u.

Таким образом, с ростом колебательной скорости возмущения, возрастает и скорость распространения возмущения. В системе отсчета, распространяющейся со скоростью с_0,

фронт сжатия укручается а , фронт разрежения растягивается.

При этом на фронте сжатия образуется “перехлест” (неоднозначность). Это предельное решение не имеет физического смысла, поскольку в одной точке в один момент времени не может быть 3 значения скорости. Эта неоднозначность означает, что решение в виде простой волны перестает существовать, а на фронте сжатия образуется разрыв.

Точка, в которой нарушается однозначность функции u(x) определяется из соотношения: . (7.16)

Для идеального газа имеем:

.,т.е. .

Надо определить, когда обращается в 0 впервые, т.е. когда минимально. Надо найти точку экстремума , отсюда определяется u, а далее и t.

Если u ( x ) задано в виде импульса, то максимально, а минимально на краю, т.е. в точке, где u = 0. Таким образом, время образования разрыва

.