лекции / Lect-11

Лекция 11

Приближение мелкой воды

Это приближение можно рассмотреть отдельно, а не как предельный случай для потенциальных волн. Рассмотрим течение жидкости средней глубины Н. Пусть на ее поверхности распространяется волна с длиной L >> Н.

Запишем проекции уравнения Эйлера

u,w — компоненты скорости.

Сделаем оценки. Пусть w ~ W; u ~ U. Тогда из уравнения неразрывности

Если масштаб по времени Т, то из 1-го уравнения

; т.е.

Сравним слагаемые во 2-ом уравнении:

; ; ; ; g

; ; ; ; g.

Отсюда видно, что всех остальных слагаемых, и ими можно пренебречь. В этом случае получается гидростатическое приближение

Если плотность постоянна, но

p = p₀ (x,t) –  gZ

На поверхности Z = h(x)t давление р = р_а , т.е.

.

Горизонтaльное лагранжево ускорение

Отсюда видно, что если в начальный момент времени горизонтальная скорость не зависела от Z, то она и не будет зависеть от Z, и горизонтальная проекция уравнения Эйлера примет вид:

Чтобы найти уравнение для h, проинтегрируем по Z от дна до поверхности уравнение неразрывности

Поскольку u не зависит от Z, a w(0) = 0

;

Учтем кинематические граничные условия на поверхности

,

тогда имеем:

Получили систему уравнений мелкой воды:

Эта система гиперболического типа. В ней возможны решения типа простых волн. В этом случае ищем решение в виде u = u(h).

Уравнение для du / dh :

; ;

Константа u₀ определяется из условия u = 0 при h = H.

;

;

Рассмотрим волну, бегущую вправо:

Скорость волны — растущая функция h (выразить скорость волны через скорость жидкости)

Из этого уравнения легко получить дисперсионное соотношение для длинных волн малой амплитуды. Пусть h = H +, где || << H, тогда линеаризация уравнения для бегущей волны дает:

Для гармонической волны  = ₀ e^{–i( t – kx)} имеем дисперсионное соотношение

 = k.

Это дисперсионное соотношение для волны без дисперсии. Все гармоники бегут с одной скоростью. Начальный импульс малой амплитуды сохраняет свою форму.

Для малой, но конечной амплитуды из уравнения для h с помощью разложения в ряд по малому параметру h/H можно получить нелинейное уравнение. Оно имеет вид:

Дополнительное слагаемое описывает эффект укручения начального импульса при распространении. Из уравнения сразу видно, что чем больше , тем больше характеристическая скорость.

Посмотрим на дисперсионное соотношение для волн на мелкой воде с другой стороны. Это волны без дисперсии. Если мы теперь учтем конечность глубины жидкости, то появится дисперсия. Дисперсионное уравнения для гравитационных волн на воде конечной глубины для волн, бегущих в одну сторону,

Пусть kH << 1, найдем разложение в ряд:

т.е.

Зная разложение в ряд дисперсионного соотношения, легко найти соответствующее ему дифференциальное уравнение. Для этого необходимо принять во внимание, что для гармонических волн

, а , тогда из дисперсионного соотношения

следует, что  удовлетворяет уравнению

;

;

Учет дисперсии приведет к тому, что разные гармоники будут иметь разные фазовые скорости, и начальный импульс будет расплываться.

Итак, мы получили, что без учета конечности амплитуды и дисперсии волн импульс для волн на глубокой водне сохраняет форму. Если учесть конечность амплитуды, то импульс укручается, если учесть дисперсию, то импульс расплывается.

Существует эвристический подход получения уравнений, описывающих эволюцию слабонелинейных слабо диспергирующих волн. Он состоит в том, что считается, что слабые нелинейность и дисперсия независимо влияют на поведение волн. При этом в уравнение для  включают нелинейные и дисперсионные добавки аддитивно. В результате получается такое уравнение:

;

Введем безразмерную переменную  = /H, тогда

.

Это уравнение называется уравнением Кортевега-де-Вриза. Оно имеет знаменитое решение — уединенную волну или солитон. Получим это решение. Это решение ищется в классе стационарных волн, т.е. волн, у которых форма не меняется в некоторой системе отсчета. Такое может получиться, поскольку в системе действуют два конкурирующих эффекта — нелинейность, укручающая фронт волны, и дисперсия, приводящая к расплыванию импульсов. Ищем решение в виде:

 =  (x – Ut) , где U = const, т.е.  =  (X), тогда .

Уравнение КдВ принимает вид:

.

Это уравнение можно проинтегрировать:

.

Поле солитона убывет при X  , т.е. const = 0. Полученное уравнение можно проинтегрировать еще раз. Для этого домножим на d / dx

;

С учетом граничных условий на  интегрирование дает

Это уравнение интегрируется в элементарных функциях. Его точное решение:  > 0

; при этом ;

Отсюда

;

Ясно, что скорость уединенной волны больше, чем скорость линейных волн на поверхности воды. Параметром в солитонном решении является амплитуда уединенной волны ₀. Она определяет ширину солитонa и его скорость С.

Чем ближе амплитуда солитона, тем он уже, и тем быстрее распространяется.

Задача о гидравлическом прыжке.

Система уравнений для мелкой воды — это гиперболическая система. Можно допустить, что могут существовать решения уравнений для мелкой воды типа ударных волн. Попробуем их найти. Будем искать решение в виде гидравлического скачка — резкого перепада уровней жидкости. Рассмотрение будем вести в СО, где скачок покоится. Скорости жидкости в слоях предполагаем постоянными по глубине (как всегда в теории мелкой воды) равными v₁ и v₂.

Рассмотрим поверхность (см. рис.) и найдем для нее законы сохранения импульса и массы. Считаем, что течение стационарно:

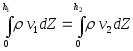
Рассмотрим вертикальную проекцию уравнения Эйлера:

p_a = const при интегрировании по замкнутой поверхности даст 0.

,

Законы сохранения массы и импульса примут вид:

Эти уравнения дают связь v₂ , h₂ при заданных h₁, v₁, как в ударной волне. Если перейти в СО, где жидкость до прохождения скачка покоится, то скачок будет двигаться со скоростью v₁. Таким образом, если мы зададим h₁ и h₂, то мы найдем скорость скачка. Исключим v₂. ;

Найдем разность потоков энергии при переходе через скачок

аналогично

=

В направлении движения жидкости поток энергии должен уменьшаться, так как внутри скачка энергия может поглощаться. Если h₁ < h₂, то g₂ < g₁, т.е. в СО, где скачок покоится, жидкость движется из мелкой стороны в глубокую. Если перейти в СО, где покоится жидкость в области h₁, то скачок движется из глубокой воды в мелкую.

Это явление наблюдается в реках и называется “бора”.

В СО, где покоится жидкость 1, а скачок движется

1. Если скачок движется со скоростью v₁.

Закон сохранения массы

;

Поток энергии, втекающей в скачок

Втекает больше, чем вытекает

2. Если скачок движется со скоростью – v₁.

Закон сохранения массы

Поток энергии в 2

Втекает 0, вытекает отлично от 0.

Это невозможно. Скачок движется из глубокой воды в мелкую.

; ;
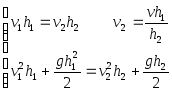