лекции / Lect-15

Лекция 15

Пограничный слой

Пусть Re >> 1. Тогда, если течение имеет достаточно большой масштаб, то можно пренебрегать вязкостью, т.е. использовать приближение идеальной жидкости. Очевидно, что это приближение нарушается вблизи твердых границ, поскольку в идеальной жидкости действует только граничное условие непротекания, а тангенциальная составляющая скорости может быть любой, и она отлична от тангенсиальной составляющей скорости движения тела. В вязкой жидкости выполняется граничное условие прилипания. Как согласовать выполнение граничных условий и пренебрежение вязкостью. Для этого Прандтлем была выдвинута гипотеза пограничного слоя. Она состоит в следующем: для достаточно широкого диапазона условий вязкость необходимо учитывать лишь в узких слоях, прилегающих к твердым границам (и в некоторых других слоях). При Re   толщина этих слоев стремится к 0. Эти слои называются пограничными слоями. Внутри пограничного слоя происходит переход от условий прилипания на поверхности к невозмущенному течению. Это предположение из разряда того: предположим, что решение имеет такой вид. Попробуем его найти. В гидродинамике такой метод применяется довольно часто ввиду сложности ее уравнений. По существу, это некоторая правдоподобная физическая модель. Найти такое решение — это большая удача. Практически может оказаться, что оно реализуется не при любых условиях; в опыте получается совершенно другое. Применимость решения ограничена. Тогда надо определить, когда это решение не применимо и почему, т.е. надо учитывать дополнительные факторы и строить дополнительные модели. Построим решение в виде пограничного слоя, а затем посмотрим, что же наблюдается в действительности.

Пограничный слой на тонкой полубесконечной пластинке.

Рассмотрим тонкую пластинку в потоке. Пусть вначале пластинки не было, тогда

Причем предположим, что v << U_p, где U₀ — масштаб скорости U. Будем считать, что масштаб изменения потока L таков, что Re = (U_pL / ) >> 1. Поместим в этот поток пластинку (это сразу дает привязку к СО). В соответствии с гипотезой Прандтля далеко от пластинки влиянием вязкости можно пренебрегать, т.е. поле скорости удовлетворяет уравнению Эйлера. Будем считать, что поле скорости далеко от пластинки потенциально. Тогда во всем потоке

(по теореме Бернулли)

И при v << U имеем

Если задан p вдоль пластинки, то известно U(x). Если бы вязкости не было, то бесконечно-тонкая пластинка не вносила бы возмущений в поток. Но на ней выполняется условие прилипания. Найдем течение, которое получается в результате.

Вблизи пластинки надо учитывать вязкость. Течение описывается системой уравнений н/с и усл. прилипания:

Перейдем к безразмерным переменным

Система уравнений примет вид:

,

— число Рейнольдса течения на пластинке. Введем функцию тока , такую, что . Уравнения в терминах функции тока имеют вид:

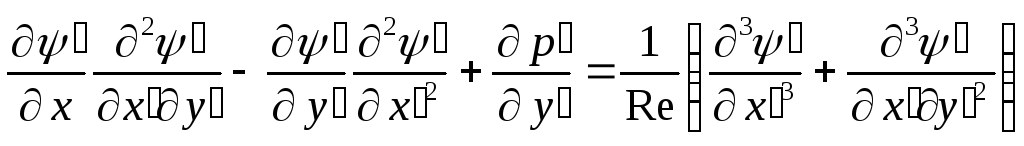
Граничные условия:

Мы рассматриваем движение в пограничном слое, где масштаб по много меньше масштаба по (1), т.е.  << 1. Тогда нужно ввести другую нормировку переменной у, т.е. переменную  = y/.

Определим  из условия, что слагаемые, входящие в уравнение н/с и описывающие движение с масштабом  << 1 , должны быть одного порядка. Сделаем оценки: u ~ 1 (т.к. y_y=0 = 0 и u_y  U/U₀ ~1).

 =

Поскольку масштаб u ~ 1 по у порядка  (такое ищем решение), то  ~ . Масштабы по x ~ 1.

Итак первое уравнение дает:

отсюда ясно, что  ~ Re^–1/2 << 1.

То есть такое решение можно искать.

Введем новые переменные

Тогда в переменных , система для функции тока примет вид:

Отсюда ясно, что величина имеет порядок Re^–1 << 1. Т.е. вертикальный градиент давления величина ~ Re^–1, т.е. можно предполагать, что p = p(x), причем p(x) определяется полем скорости далеко от поверхности, где справделива формула Бернулли, т.е. .

Пренебрегая в первом уравнении слагаемыми ~ Re^–1/2, имеем:

С г.у.

Это так называемые уравнения пограничного слоя. Найдем решение этих уравнений при условии, что , тогда U(x) постоянно: U(x) = U₀ , а . Найдем в этом случае сначала качественный вид решения. Горизонтальная скорость U() = . При y  , U()  1; при y = 0 U() = 0.

Характерный вид профиля скорости показан на рис.

Из общих соображений ясно, что толщина перехода скорости может, вообще говоря, зависеть от x. Найдем эту зависимость сначала из качественных физических соображений. Как мы видели, граница является источником завихренности. Она от границы диффундирует за счет вязкости. За время t завихренность диффундирует на расстояние . В то же время она сносится потоком (снос начинается от края пластинки). За время t частица сносится на расстояние x ~ Ut откуда t ~ X/U. Т.е. расстояние, на которое проникает завихренность, можно оценить как . Если перейти к безразмерным координатам

тогда

Итак, масштаб в безразмерных переменных по .

Будем искать так называемое автомодельное решение уравнений пограничного слоя. Т.е. такие решение, форма которых не меняется от сечения к сечению, а меняется лишь масштаб, т.е.

Такое решение, в принципе, может и не существовать, но можно попробовать его поискать.

Из граничных условий имеем . Отсюда m = 1/2.

Т.е. , где

Тогда уравнение для f примет вид

Это уравнение решается численно. Профиль скорости

(см. график)

Далеко от пластинки U = U₀. Форма кривой U(y) сохраняется. Толщина переходной области (погранслоя) растет ~).

Пограничный слой на телах, обтекаемых неоднородным потоком

Если p(x) падает, то U(x) растет. Это значит, что снос частиц происходит быстрее, чем в однородном потоке, а диффузия завихренности от твердой поверхности — с прежней скоростью. Это значит, что толщина пограничного слоя растет медленнее, чем в случае U = const (погранслой тоньше).

Если p(x) растет, то U(x) падает. В результате снос завихренности замедляется, а диффузия происходит с прежней скоростью. Это значит, что толщина пограничного слоя растет быстрее, чем в случае U = const .

В этих случаях, казалось бы, можно найти решение уравнений пограничного слоя, где U зависит от x. В случае ускоряющегося течения это действительно можно сделать, но в случае замедляющего течения, если падение U(x) происходит достаточно быстро, решение типа пограничного слоя перестает присутствовать (т.е. в решении уравнений пограничного слоя возникают особенности). Иными словами, решение, соответствующее невязкому потенциальному течению далеко от твердой поверхности с узким переходным слоем вблизи поверхности, перестает существовать. Сильно изменяется течение и вне области, прилегающей к поверхности твердого тела. Линии тока, прилегающие к границе, отклоняются от поверхности. Это явление назыается явлением отрыва пограничного слоя. Полного теоретического описания этого явления не существует до настоящего времени. В частности, не умеют находить точку отрыва погранслоя.

Рассмотрим пример обтекания сферы при Re >> 1. Казалось бы, при Re >> 1 далеко от сферы течение должно представлять собой потенциальное течение, а вблизи сферы должен образовываться погран.слой. Однако, как мы видели ранее, до точки 0 давление на поверхности сферы падает, а скорость растет, т.е. решение типа n/c существует. После точки 0 давление на поверхности сферы растет, а скорость падает. Причем падение скорости происходит достаточно быстро, так что возникает явление отрыва пограничного слоя. Вопрос состоит в том, в какой точке происходит отрыв. Это задача сложная и не решается до сих пор.

Ламинарный след

Рассмотрим обтекание тела цилиндрической формы однородным потоком. На границе тела с потоком происходит генерация завихренности (образуется погранслой, он может отрываться и т.д.). Далее эта завихренность сносится потоком и диффундирует за счет вязкости. Какое течение будет далеко за телом? Выберем координату x вдоль оси движения тела, а координату у — поперек.

Течение формируется за счет переноса завихренности и ее диффузии. За время t потоком завихренность переносится на расстояние L_k = Ut, а за счет диффузии — на расстояние , L_k — это масштаб по х; L_g — масштаб по у; ; L_k = x; при достаточно большом х L_g << L_k , т.е. течение имеет малый масштаб по у. Такое течение называется ламинарным следом. Для его описания можно применять уравнение пограничного слоя, поскольку L_y << L_x Запишем их в размерных переменных

...

Здесь р определяется свойствами течения при больших у. Поскольку мы рассматриваем обтекание тела однородным потоком, то (из уравнения Бернулли).

За счет диффузии течение "расплывается", в результате возмущения скорости малы по сравнению со скоростью основного потока, т.е.

, и

Тогда уравнение погранслоя можно линеаризовать. Тогда получим

граничные условия .

Решения уравнения диффузии, убывающее при , имеет вид:

.

О бласть возмущенного течения расширяется , т.е. ширина ламинарного следа растет .

Смысл постоянной Q.

Построим качественно график профиля в скорости U(x,y).

Ясно, что скорость внутри следа должна быть меньше U, т.к. тело экранирует поток.

Если перейти в СО, в которой тело движется, то профиль скорости в следе будет такой.

Тело увлекает за собой жидкость, т.е. есть поток массы к телу внутри следа, поскольку есть поток массы к телу, то должен быть и поток массы от тела, чтобы полный поток был равен 0. Это значит, что на большом расстоянии от тела картина течения будет такая:

Суперпозиция источника массы и течения в следе. Вычислим поток массы в следе:

,

т.е. константа Q имеет смысл объемного потока в следе жидкости к телу.