Лекция 5

5.1. Сопло Лаваля

Как все-таки добиться того, чтобы газ в сосуде двигался со сверхзвуковой скоростью? и выжимал из сосуда со сверхзвуковой скоростью? Из формулы для v(p) ясно, что надо, чтобы p_e было меньше p_* . Но этого мало, надо добиться сохранения vS(x) вдоль трубы. Поскольку зависимость v(p) немонотонная, то ясно, что этого можно добиться, только если зависимость S(x) также будет немонотонной. Такое сопло с немонотонной зависимостью S(x) называют соплом Лаваля. В нем действительно удается получить сверхзвуковой поток.

Рассмотрим задачу о течении сжимаемого газа по трубе переменного сечения более подробно. Итак, пусть задано S(x). Внешние силы и источники тепла отсутствуют. Уравнение движения жидкости по трубе (они же на трубке тока):

(5.1)

Здесь x – координата вдоль трубы в направлении потока.

Из последнего уравнения, с использованием основного термодинамического тождества

(5.2)

имеем:

(5.3)

Отсюда с учетом второго уравнения в системе (5.1) получим .

Но тогда:

Тогда 1-е и 2-е уравнения системы (5.1) принимают вид:

(5.4)

Исключая отсюда d / dx, получимсоотношение, связывающее изменение сечения сопла с изменением скорости вдоль него:

(5.4)

Определим, при каких условиях поток ускоряется, т.е. dv / dx > 0.

При v < c (в дозвуковом потоке) >0 при dS / dx < 0, т.е. сопло должно сужаться. При v > c (сверхзвуковой поток) >0 dS / dx > 0, т.е. сопло должно расширяться.

Какой это имеет физический смысл? Из уравнения Эйлера следует, что

т.е. для ускорения потока ( dv / dx > 0 ) нужен отрицательный градиент давления dp / dx < 0. В очень медленных потоках, когда v << c, и газ можно считать несжимаемым, скорость газа при уменьшении толщины трубки увеличивается (это следует из сохранения массы), а давление падает (по формуле Бернулли). При большой скорости потока (v порядка c) надо учитывать сжимаемость газа. Газ с большой скоростью поступает в узкую трубку, при этом необходимо учитывать эффект адиабатического сжатия, при котором давление растет. Возникает конкуренция эффектов гидродинамического понижения давления и адиабатического повышения. При v = c эти эффекты компенсируют друг друга. При v > c более сильным становится эффект адиабатического сжатия, поэтому при сужении трубки сверхзвуковой поток замедляется. Чтобы он ускорился, надо расширить трубку, тогда за счет понижения давления при адиабатическом расширении поток будет ускоряться.

Из этих рассуждений ясно, что для того, чтобы получить из дозвукового потока сверхзвуковой надо, чтобы газ двигался по трубке, которая сначала сужается и разгоняет его до скорости звука, а затем расширяется и разгоняет его дальше. При этом все величины: сечение трубки, давление и т.п. должны быть согласованы. Тогда течение газа будет стационарным.

Итак, качественно мы выяснили, как должно выглядеть сопло Лаваля. Рассмотрим как количественно можно рассчитать такое сопло. Пусть имеется резервуар, в котором поддерживается давление p₀, плотность ₀ при температуре T₀, давление на выходе p_e. Из сосуда выходит трубка, площадь сечения которой S(x). Рассмотрим, каким должен быть профиль сечения трубки S(x), чтобы поток на выходе из него имел заданную сверхзвуковую скорость. Удобной характеристикой потока газа является число Маха

M = v / c

В дозвуковом потоке M < 1; в сверхзвуковом M > 1. В теории сопла Лаваля принято выражать все величины как функции числа Маха. Эти формулы называются изэнтропическими. Получим их для совершенного газа. Запишем формулу Бернулли: ;(5.5)

с учетом имеем из (5.5);

(5.6)

Но v=Mc, отсюда имеем:

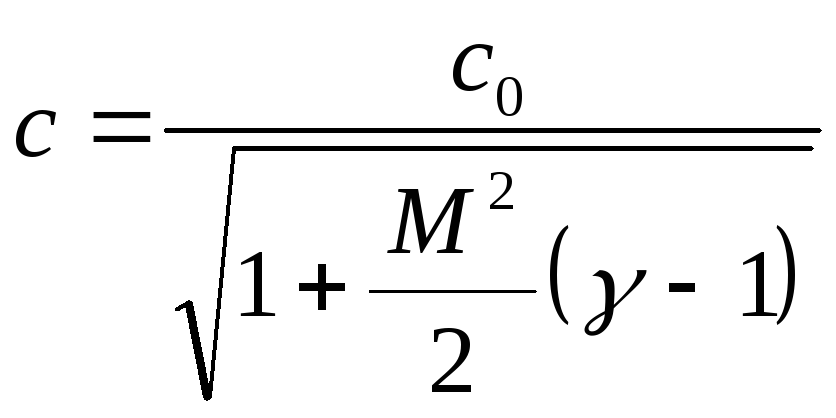, a ;

Воспользуемся тем, что

Тогда

(5.7)

С учетом уравнения адиабаты имеем из (5.7):

, (5.8)

Плотность потока газа 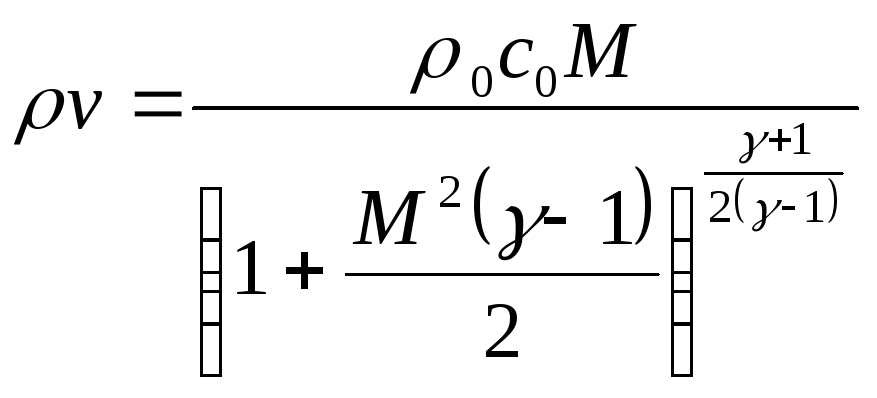(5.9)

Построим эти зависимости. с_* , v_* , _* , p_* получаются из изэнтропических формул при M=1.

Зависимости представляют собой параметрические формулы, где параметром является число Маха М. Чтобы выполнялось условие vS = Q, надо , чтобы зависимость S(M) была следующей:

(5.10)

Эта зависимость немонотонная. Она имеет минимум при М = 1.

Минимальное сечение сопла Лаваля называется критическим

(5.11)

Отсюда можно получить, что произвольное сечение зависит от М следующим образом:

(5.12)

Теперь ясно, как получить поток газа с заданными свойствами.

Пусть мы хотим получить М(x) — заданную зависимость и значение M_e на выходе.

Тогда по формуле S(M) мы находим S(x), а также все характеристики потока p, v, c,  как функции x. Они все согласованы (см.выше). Если S_* / S_e задано, то задано p_* / p_e, а поскольку p_* однозначно связано с p₀, то, значит, задано отношение p_e / p₀. Такой режим работы сопла над расчетным.

А что будет, если для заданной конфигурации сопла p_e будет другим. Подойдем к этой задаче с другой стороны. Пусть имеется сопло Лаваля с заданной формой поверхности S(x).При этом задано давление p₀ в сосуде и давление p_e на выходе из сосуда. Найдем скорость потока внутри сопла, распределение давления, плотности и т.д. Будем обозначать площадь критического сечения S_*, а площадь выходного — S_e.

Для рассмотрения удобно воспользоваться зависимостью v(p).

Из закона сохранения массы следует, что vS = const. Поскольку S зависит от x, то v также зависит от x. Мы уже получали формулу зависимости плотности потока v от давления:

Зависимость v(p) имеет вид, показанный на рисунке. Максимум зависимости имеет место при p = p^*, где v = c^*.

Когда мы перемещаемся по оси сопла, то v меняется пропорционально 1/S(x) и p меняется, т.е. мы фактически двигаемся по этой кривой.

Рассмотрим с использованием этого течения внутри сопла качественно. Нас будут интересовать распределение давления и скорости по оси сопла и характер изменения расхода через сопло Q = vS при изменении отношения p_e / p₀.

Если p_e = p₀, то v = 0, газ не течет через сопло.

Если p_e = p₁ (немного меньше p₀), то начнется истечение газа. Вдоль сечения S сначала падает, потом растет, v растет, потом падает. Зависимость v(p) монотонно падающая, поэтому v(x) ведет себя как показано на рис.

Если давление на выходе еще уменьшить (p_e = p₂), то распределение давления будет аналогичным, но более резким, а скорость истечения возрастет. При этом зависимость v(x) будет качественно такой же.

Наибольшая скорость и наименьшее давление достигаются в минимальном сечении. При этом расходе (v)_maxS_* увеличивается при переходе от зависимости 1 к 2, т.е. при уменьшении давления на выходе.

Наконец, при некотором еще меньшем значении p_e давление в самом узком сечении станет равным критическому, и поток будет равен критическому _*c_*(max). При этом расход будет максимальным _*c_*S_* . Этого можно достичь двумя способами. Стартуя с точки 3 или с точки 4 на кривой pv(). При этом при p_e = p₄ и p_e = p₃ (v)₃⁼(v)₄ , т.к. это поток через выходное сопло (одно и то же) при одном и том же потоке в критическом сечении. В первом случае получим дозвуковой, а во втором — сверхзвуковой режим. При x < x_* кривые v(x) и p(x) совпадают, поскольку двигаются по одной и той же ветке кривой v(p).

Что будет, если мы понизим выходное давление ниже p₃ (но выше p₄)? В сужающейся части трубы давление упадет от p₀ до p_*, а скорость потока вырастет до c_*. Далее в расширяющейся части трубы давление может расти, тогда поток тормозится. Но он должен тормозиться строго определенным образом, чтобы сохранялось vS. Но тогда не выполняются изэнтропические соотношения. Т.е. должны нарушаться предположения о непрерывности, стационарности, изэнтропичности и т.п., т.е. стационарное течение газа становится невозможным. Также эти предположения становятся несправедливыми при p_e < p₄, т.е. когда давление ниже, чем расчетное сверхзвуковое. При этом в сечении могут возникать скачки давления (ударные волны), течение может стать неодномерным, нестационарным. Такие режимы называют нерасчетными. Таким образом, у сопла Лаваля имеется бесконечное множество расчетных дозвуковых режимов, один расчетный сверхзвуковой режим и бесчисленное множество нерасчетных режимов, соответствующих различным значениям входного и выходного давления.