Движение шара в жидкости. Потенциальное обтекание.

Пусть шар радиуса a движется в жидкости со скоростью U. Найдем

1) поле скорости

2) распределение давления по поверхности шара

3) присоединенную массу.

Постановка задачи

Лапласиан в сферических переменных

Решение ищем методом разделения переменных

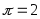
m = -2; m = 1.

При r  ; этому условию соответствует m = –2, т.е.

Из граничного условия на поверхности сферы имеем

Поле скорости

Распределение давления по поверхности сферы

Перейдем в СО, в которой тело покоится. Тогда скорость

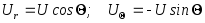
Распределение давления на поверхности сферы найдем по теореме Бернулли

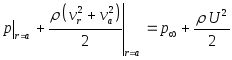
Присоединенная масса

1. Сначала находим кинетическую энергию движения жидкости.

По определению присоединенной массы

Сравнивая эти два выражения, имеем:

Присоединенная масса равна 1/2 массы жидкости в объеме тела.

Вычислим импульс жидкости непосредственно

0 — неопределенность.

Таким способом нельзя находить импульс жидкдости и присоединенную массу. А надо ее находить из кинетической энергии жидкости.