Шестаков И.Г. (513гр.)

Отчёт.

Определение коэффициента поверхностного натяжения жидкости.

Цель работы: Определение коэффициента поверхностного натяжения воды на границе раздела воздух-стекло.

ТЕОРИТИЧЕСКАЯ ЧАСТЬ

Частицы поверхностного слоя жидкости подвержены силам сцепления, равнодействующая которых не равна нулю, а направлена внутрь жидкости нормально к ее поверхности. По формуле Лапласа это поверхностное давление Р, рассчитанное на 1 см,

где К – нормальное давление на плоской поверхности, коэффициент поверхностного натяжения жидкости, R1 и R2, -главные радиусы кривизны поверхности.

R1 и R2 положительны, если они направлены внутрь жидкости ( выпуклая поверхность ).

Если в жидкость, помещенную в широкий сосуд, опустить капиллярную трубку из материала, смачиваемого жидкостью, то последняя поднимется в трубке выше уровня в широком сосуде. Если же трубка не смачивается жидкостью, то последняя опустится ниже уровня в широком сосуде. Причина этого заключается в следующем. В широком наружном сосуде можно считать поверхность жидкости плоской, поэтому нормальное давление поверх -постного слоя по формуле Лапласа равно К.

Если жидкость смачивает трубку, То поверхность жидкости внутри неё будет вогнутая. По формуле Лапласа нормальное давление в этом случае равно:

где R1 и R2, – абсолютные значения главных радиусов кривизны поверхности. Получаются избыток наружного Давления, равный

Под влиянием этого давления жидкость в капилляре поднимается на высоту h.

Если жидкость не смачивает трубку, то поверхность жидкости внутри неё выпуклая. По формуле Лапласа в этом случае поверхностное давление равно

Получается избыток давления внутри трубки. Под влияниям этого давления уровень жидкости в капилляре понизится. Пусть АВ и А'В' - стенки капилляра (рис.1), СД и ЕF – поверхность жидкости вне трубки, abc – поверхность жидкости внутри трубки. В случае смачивания избыток наружного давления над внутренним по формуле (1) равен

Если капилляр узкий, поверхность мениска можно считать сферической, т.е. R1=R2=R

тогда

Пусть 0 – центр этой сферической поверхности, – угол между стенкой и плоскостью, касательной к поверхности мениска (краевой угол). r – радиус капилляра. Тогда из треугольника имеем следовательно

(2)

Это давление уравновешивается давлением жидкости внутри трубки и равно весу столба жидкости, деленному на площадь поперечного сечения капилляра, т.е. .

Так как капилляр достаточно тонок, то последний член выражения пренебрежимо мал.

И тогда

в случае когда краевой угол равен нулю т.е. абсолютное смачивание.

Способ 1.

Для двух капилляров, радиусами r1 и r2 верно :

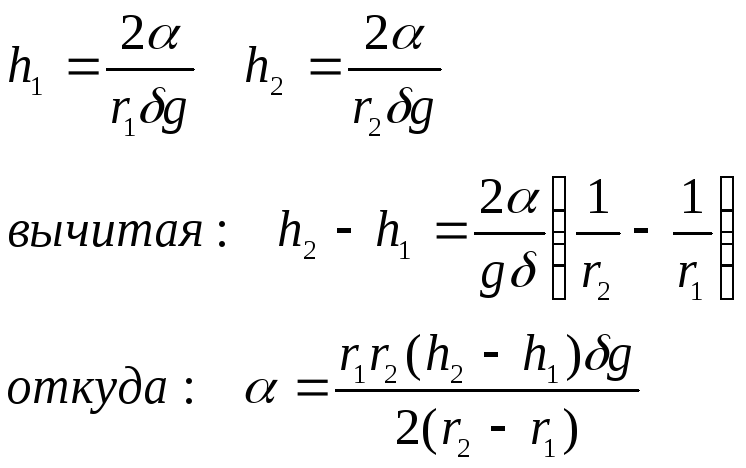
Способ 2.

Избыток наружного давления при абсолютном смачивании равен . Если скомпенсировать изменение уровня жидкости в капилляре известным давлением то можно легко определить . Для измерения давления используется жидкостной манометр с переменным углом наклона (рис2).

Давление с его помощью вычислиться как .

где - изменение положения столба жидкости.

И тогда:

Рис. 2

Практическая часть.

Приборы: стеклянные трубки различных диаметров, отсчетная трубка с окулярным винтовым микрометром (=0.06 мм), микроскоп (=0.002 мм), микроманометр (=1 мм).

1. Цена деления микроскопа составляет

Цена деления отсчетной трубки составляет

Определение диаметров трубок

№ трубки	ЧДМ	Среднее значение ЧДМ	D м
1-я трубка	473	472	944·10-6160·10-6
	471
	472
	471
	473
2-я трубка	783	782	1564·10-6265·10-6
	782
	781
	783
	782
3-я трубка	362	362	724·10-6123·10-6
	361
	363
	361
	362

(ЧДМ – число делений микроскопа, D – диаметр трубки.)

2. Определение коэффициента поверхностного натяжения воды первым способом. Для определения данной величины была использована формула указанная в теории где разности высот подъема жидкости в двух выбранных трубках, а и радиусы выбранных трубок (указаны в 1-ом пункте практической части). Экспериментально полученные данные высот подъема представлены в следующей таблице:

№ трубки	№ измерения			№ измерения
I трубка	1	511	5133	2	399	4014
		516			397
		514			403
		513			401
		512			402
II трубка	1	322	3232	2	230	2312
		325			231
		324			232
		323			233
		323			231
III трубка	1	459	4563	2	365	3643
		455			367
		457			366
		456			361
		454			363

(–число делений отсчетной трубы взятое от нуля до края поднявшейся жидкости в капиляре).

На основании полученных данных были вычислены значения

№ трубок	№ измерения			№ измерения
I-II	1	1904	1140·10-524·10-5	2	1705	1020·10-530·10-5
I-III	1	575	342·10-530·10-5	2	375	222·10-530·10-5
II-III	1	1334	798·10-524·10-5	2	1334	798·10-524·10-5

Расчет погрешностей для численного значения величины производился по следующей формуле:

На основании полученных данных были рассчитаны коэффициенты поверхностного натяжения воды:

№ трубок	№ измерения		№ измерения
I-II	1	5.2597·10-21.5779·10-2	2	4.7061·10-21.6099·10-2
I-III	1	4.0585·10-21.2175·10-2	2	3.8362·10-21.2798·10-2
II-III	1	5.0842·10-21.5761·10-2	2	5.0842·10-21.5761·10-2

Расчет погрешности для численного значения проводился по следующей формуле:

Далее все полученные результаты коэффициента поверхностного натяжения вода были усреднены по формулам для неравноточных измерений и получен окончательный результат для способа I:

3. Определение коэффициента поверхностного натяжения воды вторым способом. Для определения данной величины была использована формула указанная в теории где положение мениска в измерительной трубке при отсчете давления, начальное положение мениска, радиусы капиляров, значения указанные на дуге манометра. Экспериментально полученные данные высот подъема представлены в следующей таблице:

№ трубки
I	0.5	0.0020.001	0.060	0.0620.002	0.8	0.0050.001	0.044	0.0440.002
			0.063				0.046
			0.064				0.045
			0.063				0.043
			0.062				0.045
II	0.5	0.0020.001	0.041	0.0420.002	0.8	0.0050.001	0.031	0.0300.002
			0.042				0.029
			0.043				0.030
			0.042				0.032
			0.044				0.030
III	0.5	0.0020.001	0.088	0.0870.002	0.8	0.0050.001	0.061	0.0610.002
			0.086				0.059
			0.087				0.062
			0.086				0.060
			0.087				0.061

На основании экспериментально полученных данных были получены численные значения коэффициента поверхностного натяжения воды:

№ трубки
I	0.5	5.4869·10-21.5829·10-2	0.8	5.7064·10-21.6003·10-2
II	0.5	6.0604·10-21.7611·10-2	0.8	6.1203·10-21.5112·10-2
III	0.5	5.9616·10-21.6351·10-2	0.8	6.2842·10-21.6227·10-2

Расчет погрешности для численного значения проводился по следующей формуле:

Далее все полученные результаты коэффициента поверхностного натяжения вода были усреднены по формулам для неравноточных измерений и получен окончательный результат для способа II:

Вывод: на основании поделанных экспериментов можно заключить, что полученные численные значения коэффициента поверхностного натяжения воды первым () и вторым () способами лежат в непосредственной близости друг от друга и от табличного значения данной величины .

5