СтудФайлы vol.1 / лабы / Лабы 2 сем / Маятник Обербека

Шестаков И.Г. (гр. 513)

Отчёт

Маятник Обербека.

Маятник Обербека (рис. 1) состоит из четырёх стальных спиц, вставленных во втулку. втулка скреплена со шкивом и горизонтальной осью, которая может вращаться в подшипниках. Цилиндрические грузы одинаковой массы можно перемещать вдоль спиц и закреплять винтами. На шкив намотана нить с грузом на конце. При падении груза нить разматывается и приводит во вращение прибор.

Найдём закон движения маятника. На маятник действует сила натяжения нити

, создающая относительно оси вращения момент (-радиус шкива) и сила трения, создающая момент . Следовательно, уравнение моментов относительно оси вращения для маятника может быть записано в виде:

Из второго закона динамики для падающего груза

так как , то

подставляя (2) в (1), получим

или обозначая

Считая момент трения постоянным, а начальную скорость равной нулю, найдём из соотношения (3) зависимость угла поворота маятника от времени:

Пусть груз падает с высоты за время 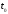. Длина нити , а угол поворота маятника до полного раскручивания нити

следовательно

Для нахождения рассмотрим изменение энергии при движении маятника. В начальном состоянии нить намотана на шкив, груз поднят на высоту , кинетическая энергия маятника и груза равна нулю. Затем нить разматывается, и груз опускается. Маятник и груз приобретают кинетическую энергию

за счёт работы силы тяжести, равной, и работы силы трения .

Следовательно,

Так как маятник продолжает вращаться, нить снова наматывается на шкив, и груз поднимается, как показывает опыт, на высоту . Приращение кинетической энергии при этом равно

складывая (7) и (8), получим

или

Подставляя полученное выражение для в (6), найдём

откуда

соотношение (10) позволяет вычислить по результатам измерений

Практическая часть.

Приборы: метровая линейка (δ=1 см), секундомер (δ=0.2 с), штангенциркуль (δ=0.05 мм), грузы на спицах, груз на нитке.

При расчете всех погрешностей использовалась доверительная вероятность .

1. В рассмотренной теории маятника Обербека делалось предположение, что при постоянных массе груза (), подвешенного на нити, и радиуса шкива () момент силы трения остаётся постоянным. Проверим это предположение экспериментально. Для этого будем изменять высоту подъёма груза () и измерять повторную высоту подъёма (). Если отношение высот в формуле (9) будет оставаться постоянным то наше предположение окажется верным.

В результате проведённых экспериментов были получены следующие результаты:

1.300.02	1.18	0.580.02	0.900.02	1.02	0.420.02
	1.20			1.03
	1.16			1.01
	1.19			1.01
	1.19			1.02
1.100.02	1.11	0.500.02	0.700.02	0.94	0.320.02
	1.10			0.92
	1.11			0.91
	1.10			0.92
	1.09			0.91

Подставив полученные результаты в выражение , были получены численные значения данной величины, которые представлены ниже

1.300.02	0.580.02	0.380.02
1.100.02	0.500.02	0.380.02
0.900.02	0.420.02	0.370.02
0.700.02	0.320.02	0.370.03

Расчет погрешностей для величины производился по следующим формулам:

Из экспериментально полученных результатов можно сделать вывод, что теоретическое предположение о постоянстве момента силы трения оказалось верным.

2. В данном задании требовалось определить: 1. Момент инерции маятника без грузов; 2.момент инерции маятника с грузами, закрепленными в середине спиц; 3. Момент инерции маятника с грузами, закрепленными на концах спиц. Расчет моментов инерций производился по формуле (10). Все экспериментально полученные данные, необходимые для расчетов представлены ниже:

Во всех проведенных опытах начальная высота подъема составляла .

№			№
1	0.50	3.2	3	0.44	8.8
	0.50	3.2		0.45	9.0
	0.51	3.2		0.46	8.8
	0.50	3.0		0.45	8.8
	0.49	3.0		0.44	9.0
2	0.46	6.0
	0.47	6.0
	0.45	6.2
	0.46	6.0
	0.45	6.2

После подстановки численных значений в формулу (10) были получены следующие результаты:

№
1	0.02680.0036	0.1329
2	0.08890.0073	0.0835
3	0.18830.0126	0.0671

Расчет погрешностей для численных значений моментов инерции производился по следующим формулам:

Из полученных результатов можно сделать вывод, что с подвешиванием грузов на спицы маятника Обербека его момент инерции увеличивается. Так же видно, что с увеличением расстояния грузов от оси вращения, момент инерции маятника увеличивается.

3. В данном задании требовалось проверить, выполняется ли на опыте пропорциональность между (моментом инерции грузов) и (квадратом расстояния до оси вращения). Вследствие того, что момент инерции величина аддитивная расчет производился по следующей формуле , где –момент инерции маятника с грузами закреплёнными на расстоянии , а –момент инерции маятника без грузов (рассчитан в предыдущем задании). Расчет моментов инерции производился по формуле (10). Все экспериментально полученные данные, необходимые для расчетов представлены ниже:

Во всех проведенных опытах начальная высота подъема составляла .

0.290.01	0.44	8.8	0.170.01	0.46	6.0
	0.45	9.0		0.47	6.0
	0.46	8.8		0.45	6.2
	0.45	8.8		0.46	6.0
	0.44	9.0		0.45	6.2
0.250.01	0.44	7.8	0.130.01	0.43	5.4
	0.46	8.0		0.42	5.4
	0.45	8.0		0.43	5.4
	0.45	7.8		0.42	5.4
	0.44	8.0		0.44	5.6
0.210.01	0.43	7.0	0.090.01	0.45	4.6
	0.44	7.2		0.43	4.6
	0.44	7.2		0.44	4.4
	0.43	7.0		0.43	4.4
	0.43	7.0		0.44	4.4

4. Подставив численные значения в формулу (10) были получены следующие значения момента инерции маятника:

0.290.01	0.18830.0126	0.0671
0.250.01	0.15560.0109	0.0702
0.210.01	0.11530.0088	0.0767
0.170.01	0.08890.0073	0.0835
0.130.01	0.06860.0062	0.0901
0.090.01	0.04630.0046	0.1038

Расчет погрешностей для моментов инерции производился по формулам, представленным во втором задании.

4. Далее по на основании полученных результатов моментов инерции маятника были рассчитаны моменты инерции грузов расположенных на расстоянии по следующей формуле :

0.290.01	0.16150.0131
0.250.01	0.12880.0115
0.210.01	0.08850.0095
0.170.01	0.06210.0082
0.130.01	0.04180.0072
0.090.01	0.01950.0059

Расчет погрешности для момента инерции грузов производился по следующей формуле:

4. Для, экспериментально полученных, численных значений момента инерции грузов была построена зависимость от 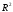, которая представлена ниже:

Рассчитаем коэффициент корреляции (G) для полученной зависимости по формуле:

где пар числовых значений, полученных экспериментально (i=1,…); и средние статистические результаты измерений.

Подставив, экспериментально полученные, численные значения в выражение получим численное значение приближенного значения коэффициента корреляции:

G=0.996

Оценка коэффициента корреляции, столь близкая к единице, является убедительным доказательством наличия линейной зависимости между величинами.

Из полученных результатов можно сделать вывод, что наличие линейной зависимости между величинами и является экспериментальным доказательством теоретической пропорциональности данных величин.

4. Расчет численного значения момента силы трения (). При оценке численного значения момента силы трения были использованы экспериментальные данные, которые были получены при подтверждении его постоянства. После подстановки численных значений в формулу (9) были получены следующие результаты:

Расчет погрешностей для каждого момента трения производился по следующим формулам:

Выводы:

1. В первом задании из экспериментально полученных результатов видно, что теоретическое предположение о постоянстве момента силы трения оказалось верным.

2. Во втором задании нетрудно заметить, что для полученных экспериментальных результатов выполняется следующая закономерность. С подвешиванием грузов на спицы маятника Обербека его момент инерции увеличивается. Так же видно, что с увеличением расстояния грузов от оси вращения, момент инерции маятника увеличивается.

№
1	0.02680.0036	0.1329
2	0.08890.0073	0.0835
3	0.18830.0126	0.0671

где 1–момент инерции маятника без грузов; 2–момент инерции маятника с грузами, закрепленными в середине спиц; 3–Момент инерции маятника с грузами, закрепленными на концах спиц.

3. В третьем задании из полученных результатов можно сделать вывод, что наличие линейной зависимости между величинами и является экспериментальным доказательством теоретической пропорциональности данных величин.

4. В четвертом задании был определен момент силы трения для данной установки, численно равный .

7