СтудФайлы vol.1 / лабы / Мои лабы / Адиабата

Министерство обра­зования Российской Федерации

Нижегородский государ­ственный университет им. Н.И.Лобачевского

Физический факультет

ОТЧЕТ

по лабораторной работе

«Определение адиабатической

постоянной воздуха»

Выполнил:

студент группы №511

Кучин Д.П.

Проверил:

Позднеев Д.Б.

г. Нижний Новгород

2004 г.

Цель работы: Измерение адиабатической постоянной воздуха двумя методами: методом кле­мана-дезорма и методом измерения скорости звука.

Теоретическая часть.

Теплоемкость системы в заданном процессе определяется как отношение количестве пе­реданной системе теплоты к изменению ее температуры:

Из этого определения следует, что теплоемкость является дифференциальной характери­стикой бесконечно малого процесса. Эта величина зависит от массы системы, ее молекулярного строения, от начальных условий и, наконец, от условий теплообмена. Процесс теплообмена можно осуществить множеством способов и каждый из них характеризуется своим значением С. Важную роль в физике огреют теплоемкости при иэохорическом (Сv ) и изобарическом (Ср) нагревании газа. Эти величины определяют значение показателя адиабаты , нахождение которого для воздуха в составляет цель настоящей работы.

Определение γ методом клемана-дезорма.

Уравнения процессов, с которыми придется иметь дело в настоящей работе, записывают обычно для фиксированной массы газа. Однако в предстоящем опыте полная касса газа в сосу­де будет изменяться. В подобных случаях удобнее оперировать с удельным объемом V, кото­рый определяется как объем, занимаемый единичной массой газа V = V0/m, где V - занимаемый газом объем, а m - его масса. Выделяя мысленно единичную массу воздуха, которая при всех изменениях остается внутри сосуда, для адиабатического процесса можно записать

PV^γ= const (1)

Уравнение изотермы в этих обозначениях имеет вид

PV= const (2)

В ходе дальнейшего изложения мы везде будем пользоваться именно удельным объе­мом.

Описание установки и эксперимента.

Большой стеклянный сосуд при помощи крана может сообщаться о наружным воздухом.

Через трубку он соединяется с водяным манометром, а через другую трубку - с нагнета­тельным насосом.

Закроем кран К и накачаем в сосуд воздух; при этом его удельный объем уменьшится, а давление и температура повысятся по сравнению со значениями этих параметров для воздуха в комнате (P0,V0). Процесс изменения состояния воздуха в сосуде на данной стадии опыта изо­бражается на плоскости (P,V) кривой 0 1 (рис. 2). Через несколько минут выдержки темпера­тура воздуха в сосуде уменьшатся до комнатной (T0), а давление несколько снизится; воздух изохорически переходит из состояния 1 в состояние 2, лежащее на пересечений изотермы T0 и изохоры V1. Если теперь открыть ненадолго кран К, то воздух в сосуде станет расширяться до тех пор, пока его давление не сравняется с атмосферным, после чего кран закрывают. Ввиду скоротечности этого процесса модно пренебречь теплообменом между воздухом в сосуде и комнате и считать расширение газа 2  3 адиабатическим. Спустя некоторое время температу­ра воздуха сравняется с комнатной, причем процесс выравнивания температур протекает изохори­чески (34).

В адиабатическом процессе бесконечно малые изменения параметров P и V связаны меж­ду собой соотношением

(3)

которое получается путем взятия дифференциалов от обеих частей формулы (1). Соотношение (3), переписанное в виде

(4)

определяет направление касательной к адиабате в точке с координатами (P,V). Учитывая отно­сительную малость изменений давления и удельного объема в описанном опыте, можно счи­тать, что участок кривой (2  3) на рис.2 практически совпадает с отрезком касательной к адиабате в точке 2. Выражая тангенс угла наклона отрезка (2  3) через конечные разности, получим вместо (4)

(5)

Применяя аналогичные рассуждения к состояниям 2 и 4, лежащим на изотерме Т0, т.е. дифференцируя (2) и заменяя дифференциалы конечными разностями, найдем

(6)

Исключим теперь из (5), (6) неизвестное отношение P2/V1 и выразим 

(7)

Входящие сюда разности давлений определяются, очевидно, соответствующими показа­телями манометра в состояниях 2 и 4:

; (8)

(коэффициент k в (8) зависит лишь от плотности жидкости в манометре). После подстановки (8) в (7) получаем формулу, которая выражает искомый показатель адиабаты  через измеряемые величины

(9)

Замерим эти величины на установке и найдем γ для каждого измерения, принимая во внимание, что:

и

Найдем  методом нахождения средневзвешенного значения. Предварительно следует отметить, что погрешности для каждой из 5 рассчитываются исходя из приборных погрешно­стей:

h2, м	0,409	0,405	0,425	0,348	0,398
h4, м	0,340	0,340	0,344	0,326	0,337
γ	1,29	1,308	1,296	1,273	1,279

Результирующая погрешность  находится как средневзвешенное.

 = 1,289

 = 0,021

Определение γ методом измерения скорости звука.

Скорость распространения звуковой волны в воздухе υ зависит от атмосферного давле­ния , плотности воздуха и от величины адиабатической постоянной . Эта зависимость вы­ражается формулой

(10)

Для определения , как видно из (10) необходимо установить значения величин , , υ.

В настоящей работе измеряется скорость распространения монохроматической звуковой волны, источником которой служит динамик, запитываемый от генератора синусоидальных на­пряжении (он называется звуковым генератором - ЗГ). Чтобы понять сущность эксперимента, необходимо иметь в виду, что плоская монохроматическая волна представляет собой периоди­ческие колебания давления воздуха, передающиеся с определенной скоростью от одной точки пространства к другой. Это значит, что если в некоторой точке, например, в начале координат, давление изменяется во времени по закону

то на расстоянии x. от начала в направлении распространения волны точно такое же колебание будет наблюдаться по истечении времени  = x/υ. Таким образом, запаздывание колебания в точке x определяется временем, за которое волна проходит расстояние x. Поэтому

(11)

Уравнение (11) выражает то наиболее характерное свойство плоской монохроматиче­ской волны, что фаза соответствующего колебания линейно возрастает в направлении ее рас­пространения

(12)

Расстояние, на котором фаза изменяется на 2, называют длиной волны . Согласно этому определению,  = 2/ = T и дело сводятся к измерению , потому что период колеба­ний в волне задается звуковым генератором.

(13)

М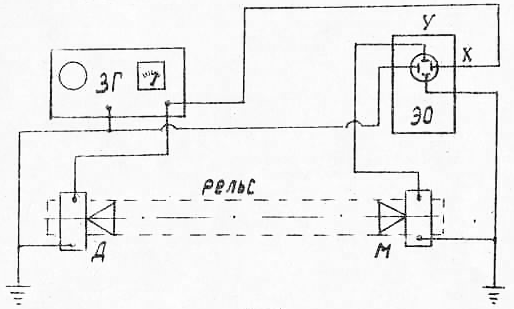етод измерения  основывается на том, что бы установить минимальное расстояние между точками, в которых колебания давления происходят синфазно. Это достигается следую­щим образом. Колебания с ЗГ подаются на горизонтально отклоняющие, а колебания, регист­рируемые микрофоном, - на вертикально отклоняющие пластины осциллографа.

В результате суперпозиции вза­имно перпендикулярных гармонических колебаний луч на экране осциллографа будет вычерчивать эллипс, форма и ори­ентация которого зависят от фазы сиг­нала с микрофона. При перемещении микрофона вдоль рельсов фаза колеба­ния с микрофона будет изменяться со­гласно (12), в то время как фаза сигнала с ЗГ остается неизменной.

Найдем значения длин волн, со­ответствующие нескольким частотам:

ν, Гц	4000	5000	6000	7000	8000
λ, см	9,5	7,5	6	5	4,5
	9	7,5	6	5	4,4

Методом наименьших квадратов найдем , по формулам (10) и (13), принимая во внима­ние, что коэффициент, получаемый этим методом, имеет вид:

k фактически имеет смысл скорости звука в воздухе.

k = 345,81 м/с

k = 20,27 м/с

Выразим отсюда :

 = 1,41

Погрешность находится тем же методом:

так как и близки к нулю, то

 = 2_k

 =0,16

Вывод:

Исследуя адиабатическую постоянную воздуха двумя методами: метод клемана-дезорма и метод измерения скорости звука, можно прийти к заключению, что они оба дают приемлемые результаты, которые лишь незначительно отличаются от табличного значения этой величины. Дос­таточно большая погрешность в методе измерения скорости звука объяс­няется особенностями обработки исходной таблицы методом наименьших квадратов: величина, откладываемая по оси X составляется из последо­вательной суммы значений измерений длин волн, приведенных в таблице данных рассматриваемого метода, соответствующих выбранной частоте.