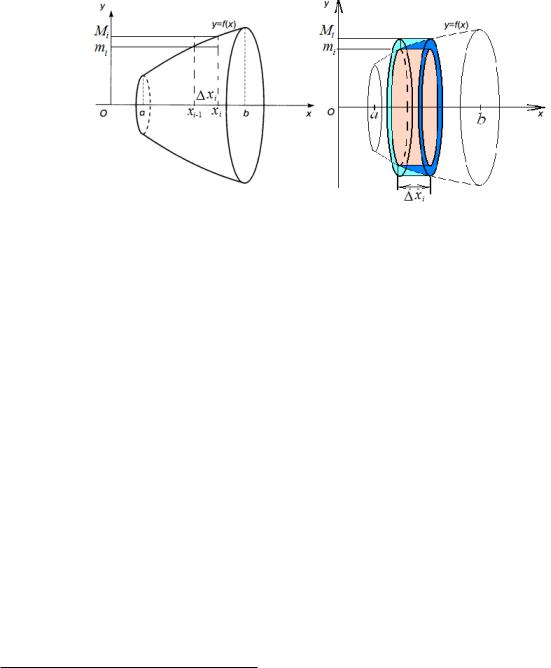
Лекция 20. Тело вращения

20.1.Объем тела вращения

Пусть функция y = f(x) непрерывна и неотрицательна на отрезке [a; b]. Тело T, образованное вращением вокруг оси абсцисс криволинейной трапеции

= f(x; y) : a x b; 0 y f(x)g;

называется т е л о м в р а щ е н и я.

Рис. 1: Тело вращения.

Теорема 20.1.1. Тело вращения кубируемо и его объем выражается формулой

Доказательство. Разобьем отрезок [a; b] на частичные отрезки точками a = x0 < x1 < : : : < xn = b:

Пусть mi è Mi точные грани f(x) на частичном отрезке [xi 1; xi]. На каждом таком отрезке построим два прямоугольника с высотами mi è Mi (íà ðèñ. 1 эти прямоугольники изображены только на одном отрезке [xi 1; xi]). В результате получатся две многоугольных фигуры, одна из которых содержится в криволинейной трапеции, а другая содержит ее. При вращении криволинейной трапеции и этих многоугольных фигур мы получим тело T и два ступенчатых1 тела, являющихся объединением конечного числа круговых

цилиндров, одно из которых Q содержит T, а другое P содержится в T. Очевидно, объемы тел Q и P равны соответственно

XX

1Ступенчатым телом называется объединение конечного числа цилиндрических тел, расположенных так, что верхнее основание каждого предыдущего из этих тел находится в одной плоскости с нижним основанием последующего.

1

Легко видеть, что эти выражения представляют собой верхнюю и нижнюю суммы Дарбу для функции f2(x). Поскольку эта функция интегрируема, то разность указанных сумм

для некоторого разбиения отрезка [a; b] будет меньше наперед взятого положительного числа ". Следовательно, согласно теореме 19.2.2 тело T кубируемо. Поскольку предел ука-

b

занных сумм при стремлении диаметра разбиения отрезка [a; b] к нулю равен R f2(x) dx,

a

то объем V = jTj тела T вычисляется по формуле (20.1).

Пример 20.1. Найти объем V шара радиуса r. Рассмотрим этот шар как результат враще- p

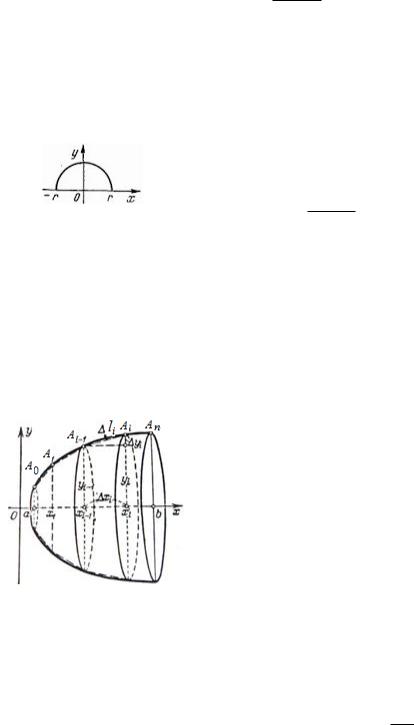
ния криволинейной трапеции, ограниченной полуокружностью y = r2 x2, r x r, вокруг оси Ox (рис. 2). По формуле (20.1) получим

p

Рис. 2: Криволинейная трапеция = f(x; y) : r x r; 0 y r2 x2g.

20.2.Площадь поверхности вращения

Пусть нам дана поверхность, образованная вращением кривой , описываемой в прямоугольной системе координат xOy функцией y = f(x), a x b, вокруг оси Ox. Функцию f(x) предположим непрерывной и имеющей непрерывную производную во всех точках отрезка [a; b]. Определим площадь этой поверхности на промежутке a x b.

Рис. 3: Тело вращения.

Для этого произведем разбиение отрезка [a; b] на частичные отрезки точками

a = x0 < x1 < : : : < xn = b:

Обозначим xi длину частичного отрезка [xi 1; xi], ( ) = max xi диаметр разбиения

i=1;n

отрезка [a; b]. Впишем в кривую ломаную n с вершинами Ai(xi; yi), ãäå yi = f(xi), i = 0; n (ðèñ. 3). Длины звеньев A0A1, A1A2, : : :, An 1An ломаной обозначим через `1, `2, : : :,

`n.

2

Каждое звено ломаной длины `i (i = 1; n) при вращении опишет усеченный конус, площадь поверхности2 Pi которого равна

данного положительного числа " можно указать такое положительное число , что для любого разбиения отрезка [a; b], диаметр которого меньше , выполняется неравенство

8 " > 0 9 > 0 : 8 [a; b]; ( ) < ) jPn P j < ":

Поверхность вращения называется к в а д р и р у е м о й, если существует предел P площадей Pn. При этом число P называется п л о щ а д ь ю рассматриваемой п о в е р х н о с т и.

Заметим, что сумма (20.2) не является интегральной суммой для функции

p

2 f(x) 1 + f02(x); (20.3)

так как в слагаемом, соответствующем отрезку [xi 1; xi], фигурирует несколько точек этого отрезка xi 1, xi, i.

2За площадь боковой поверхности конуса принимается площадь развертки его боковой поверхности.

Поэтому площадь боковой поверхности прямого

кругового конуса равна площади соответствующего кругового сектора (Sá.ê. = 12L2') с централь-

R

ным углом ' = 2 L и вычисляется по формуле Sá.ê. = RL; ãäå R радиус основания, a L длина

образующей конуса.

Аналогично за площадь боковой поверхности усеченного конуса принимается площадь соответствующей развертки. Поэтому в случае прямого кругового конуса площадь боковой поверхности усеченного конуса вычисляется по формуле

= (r1 + r)l; ãäå r1 è r радиусы оснований, a l длина образующей усеченного конуса.

3

Теорема 20.2.1. Если на отрезке [a; b] функция f(x) имеет непрерывную производную f0(x), то поверхность, образованная вращением графика этой функции вокруг оси Ox, квадрируема и ее площадь P может быть вычислена по формуле

Доказательство. Докажем, что предел суммы (20.2) равняется пределу интегральной суммы для функции (20.3), ò. å.

Действительно, Pn можно представить в виде суммы:

выражения (20.6) представляет собой интегральную сумму функции (20.3), которая, в

Замечание 20.1. Если поверхность получается посредством вращения вокруг оси Ox кривой , определяемой параметрическими уравнениями

x = x(t); y = y(t); t ;

4

где x(t), y(t) непрерывно дифференцируемы на [ ; ], то осуществляя замену переменных

под знаком определенного интеграла в формуле (20.4), получим следующее выражение для площади P этой поверхности

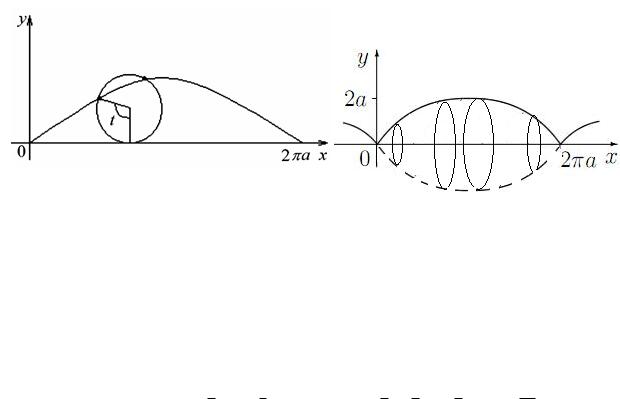
Пример 20.3. Найдем площадь P поверхности, образованной вращением вокруг оси Ох циклоиды, определяемой параметрическими уравнениями

x = a(t sin t); y = a(1 cos t); 0 t 2 :

Ц и к л о и д а плоская кривая, которую описывает точка окружности радиуса a, катящаяся без скольжения по прямой линии (рис. 4).

Рис. 4: Циклоида и поверхность, образованная вращением циклоиды вокруг Ox.

По формуле (20.7) имеем

Òàê êàê x0(t) = a(1 cos t), y0(t) = a sin t, то согласно формуле (20.4)

Замечание 20.2. Формулы (20.4) è (20.7) можно единообразно записать в виде

где d` дифференциал дуги, A, B граничные точки кривой вращения. Эта формула справедлива и в случае, если кривая расположена ниже оси Ox.

5