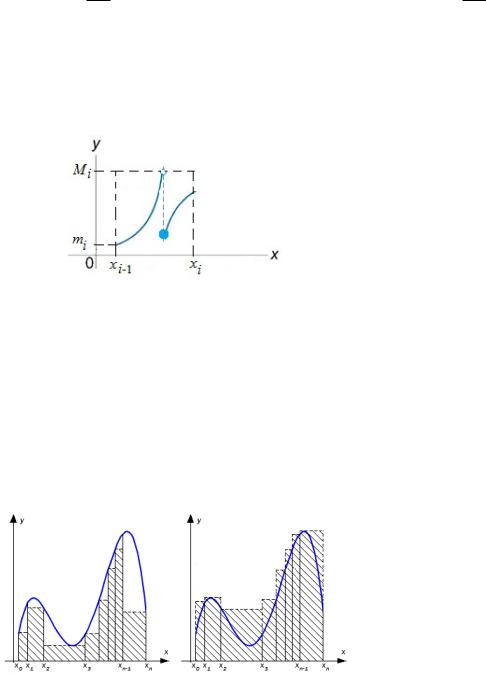
Лекция 9. Суммы Дарбу и их свойства

9.1.Нижняя и верхняя суммы Дарбу

Пусть функция f(x) ограничена на отрезке [a; b] и = fx0; x1; : : : ; xng некоторое разбиение отрезка [a; b].

Так как f(x) ограничена на отрезке [a; b], то она ограничена на каждом частичном

отрезке разбиения [xi 1; xi], i = 1; n. Следовательно, существуют числа mi, Mi (i = 1; n), являющиеся соответственно точной нижней и точной верхней гðàíями множества значе- ний f(x) на соответствующем частичном отрезке [xi 1; xi] (i = 1; n):

Рис. 1: Точные грани множества значений f(x) на отрезке [xi 1; xi]

Определение 9.1. Назовем нижней суммой Дарбу, соответствующей разбиению , вы-

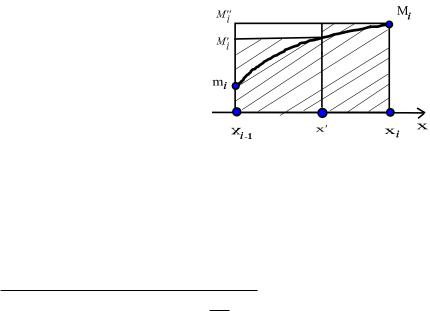
Рис. 2: Геометрическая интерпретация нижней и верхней сумм Дарбу.

Замечание 9.1. Cуммы Дарбу, вообще говоря, не совпадают с интегральными суммами. Как видно из рис. 1 точная верхняя грань множества значений f(x) на отрезке [xi 1; xi] не достигается. Поэтому при любом выборе точки i 2 [xi 1; xi] имеем f( i) 6= Mi.

1

9.2.Свойства сумм Дарбу

1.О связи сумм Дарбу с интегральными суммами. Пусть задано разбиение отрезка

[a; b] è ( ) интегральная сумма, отвечающая данному разбиению 1. Тогда при

любом выборе промежуточных точек i справедливы неравенства s ( ) S;

ãäå s è S соответственно нижняя и верхняя суммы Дарбу, отвечающие тому же разбиению. Более того

s = inf ( ); S = sup ( );

Поэтому имеем следующие соотношения:

nn

PP

(a) 8 = f 1; : : : ; ng ( ) = f( i) xi mi xi = s;

i=1 i=1

(b) 8" > 0 9 = f 1; : : : ; ng :

означающие, что s = inf ( ) при фиксированном разбиении отрезка [a; b].

Д/З: Доказать, что S = sup ( ) при фиксированном разбиении отрезка [a; b].

2. При добавлении в разбиение = fx1; : : : ; xng отрезка [a; b] новых точек верхняя сумма S не увеличивается, а нижняя сумма s не уменьшается.

Рис. 3: Иллюстрация свойства 2.

Доказательство читайте в [1] на стр. 331 332 (свойство 2 ). Èç ðèñ. 3 видно, что точная верхняя грань функции на части отрезка [xi 1; xi] не превосходит точную

верхнюю грань Mi этой функции на всем отрезке [xi 1; xi]. Очевидно, что при добавлении точки x0 в разбиение верхняя сумма Дарбу уменьшится на величину

площади незаштрихованного прямоугольника.

1Если разбиение отрезка [a; b] задано, то интегральные суммы зависят только от выбора точек i íà

частичных отрезках [xi 1; xi], i = 1; n; = f 1; : : : ; ng.

2

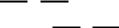
3.Нижняя сумма Дарбу для функции f(x) на отрезке [a; b] не превосходит верхнюю

сумму Дарбу всегда, даже если они соответствуют различным разбиениям отрезка [a; b].

Доказательство. Пусть 0 è 00 некоторые разбиения отрезка [a; b] и разбиение отрезка [a; b], содержащее все точки разбиений 0 è 00, при этом общие точки разбиений 0 è 00 учитываются один раз:

= 0 [ 00:

Докажем, что s( 0) S( 00). Cогласно свойствам 1 и 2 справедливы неравенства

свойство 2

z }| {

s( 0) s( ) S( ) S( 00);

|{z }

свойство 1

что и требовалось доказать.

Следствие 9.2.1. Множество fsg нижних сумм Дарбу, данной функции f(x), отвечающих всевозможным разбиениям отрезка [a; b], ограничено сверху. Множество fSg верхних сумм Дарбу ограничено снизу.

Действительно, любая нижняя сумма s( ) не больше любой фиксированной верхней суммы, следовательно, множество нижних сумм fsg ограничено сверху любой верхней суммой S. Аналогично проводятся рассуждения для верхних сумм.

В силу теоремы о существовании точных граней ограниченного множества существуют точная верхняя грань множества fsg и точная нижняя грань множества fSg.

Определение 9.2. Точную верхнюю грань множества нижних сумм fsg данной функции f(x) для всевозможных разбиений отрезка [a; b] называют н и ж н и м и н -

ò å ã ð à ë î ì Ä à ð á ó:

supfsg , I :

Точную нижнюю грань множества верхних сумм fSg данной функции f(x) для всевозможных разбиений отрезка [a; b] называют в е р х н и м и н т е г р а л о м Д а р -

á ó:

inffSg , I :

4. Нижний и верхний интегралы Дарбу удовлетворяют соотношению

I I :

Доказательство. Так как множество нижних сумм fsg ограничено сверху любой

верхней суммой S (S верхняя грань множества fsg) и I = supfsg, то согласно

определению точной верхней грани числового множества число I есть наименьшая из всех верхних граней этого множества: I S для всех S, а, значит, I является нижней гранью множества fSg.

Поскольку I = inffSg и нижняя грань множества не превосходит точной нижней

грани множества, то I I .

3

Список литературы

[1]Ильин В.А., Позняк Э.Г. Основы математического анализа: В 2-х ч, Часть 1. М.: ФИЗМАТЛИТ, 2005.

[2]Кудрявцев Л.Д. Математический анализ Òîì 1.

4