интегрирование / Лекция13.Интеграл с переменным верхним пределом, формула Ньютона-Лейбница

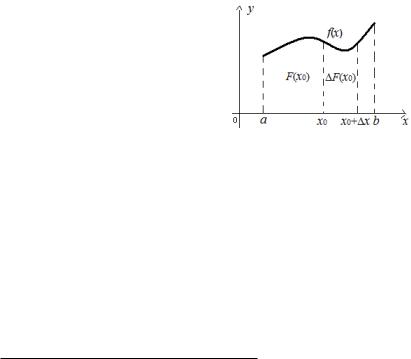
Лекция 13. Интеграл с переменным верхним пределом, формула Ньютона Лейбница

13.1.Определенный интеграл как функция переменного верхнего предела

Пусть функция f(x) интегрируема на отрезке [a; b], тогда1 она интегрируема и на лю-

a

которую называют и н т е г р а л о м с п е р е м е н н ы м в е р х н и м п р е д е л о м.

Теорема 13.1.1 (Непрерывность интеграла с переменным верхним пределом) . Если функция f интегрируема на [a; b], то функция (13.1) непрерывна на этом отрезке.

Доказательство. Пусть x0, x0 + x 2 [a; b]. Тогда

Рис. 1: Геометрическая интерпретация интеграла с переменным верхним пределом.

Функция f ограничена на [x0; x0 + x] (поскольку она интегрируема), поэтому согласно

x0+ x

Z

f(t)dt = x:

x0

Следовательно, в произвольной точке x0 2 [a; b] приращение функции F (x0) = x стремится к нулю при x ! 0, откуда следует непрерывность функции F . Теорема доказана.

1Лекция 11-12, пункт 11.1, свойство 3.

1

Теорема 13.1.2 (Дифференцируемость интеграла с переменным верхним пределом) . Если функция f непрерывна на интервале (a; b), то функция (13.1) дифференцируема на

этом интервале.

Доказательство. Пусть x0, x0 + x 2 (a; b). Согласно формуле (13.2) и следствию 11.4.2 приращение функции F в точке x0 равно F (x0) = f( ) x; ãäå 2 [x0; x0 + x]. Тогда

тервале (a; b), что и требовалось доказать.

Доказанные теоремы показывают, что операция интегрирования с переменным верх-

ним пределом приводит к улучшению свойств функции: из интегрируемой функции

получается непрерывная функция, а из непрерывной функции получается дифференцируемая.

Напомним, что операция дифференцирования в определенном смысле ухудшает свой-

ства функции: например, производная непрерывной функции, если она существует, может быть уже разрывной функцией2.

Замечание 13.1. Если функция f непрерывна на отрезке [a; b], то функция (13.1) дифференцируема на интервале (a; b) и в точках a, b существуют соответствующие односторонние производные. В точках x0 = a è x0 = b приведенные выше рассуждения достаточно применить для x > 0 и x < 0, соответственно.

Замечание 13.2. При доказательстве теоремы 13.1.2 мы установили, что производная от интеграла с переменным верхним пределом от непрерывной функции равна подинтегральной функции в точке верхнего предела:

p0

Так как функция f(t) = 2 + t2 непрерывна, то согласно формуле (13.3) имеем

Данная функция сложная функция, в которой внешняя функция интеграл с пе- p

x. Применяем формулу (13.3)

2Об этом мы уже говорили в первом семестре: лекция 28, пункт 28.4, замечание 28.3.

2

Замечание 13.3. Из формулы (13.3) дифференцирования по верхнему пределу легко получить и формулу дифференцирования по нижнему пределу, так как 3

Z b Z x

f(t) dt = f(t) dt:

xb

Производная от этого интеграла по x, очевидно, равна f(x) (если x есть точка непрерывности).

Следствие 13.1.3. Если функция f непрерывна на интервале (a; b), то она имеет на

этом интервале первообразную4, причем одной из ее первообразных является интеграл с переменным пределом (13.1), ò. å.

a

Действительно, поскольку в любой точке x 2 (a; b) функция (13.1) дифференцируема и имеет место равенство (13.3), то функция (13.1) является первообразной функции f. Таким образом, установлена связь между неопределенным и определенным интегралом.

Замечание 13.4. Утверждение 13.1.3 справедливо не только для интервала, но и для полуинтервала или отрезка, если под производной функции (13.1) в граничной точке, принадлежащей рассматриваемому промежутку, понимать соответствующую одностороннюю производную.

Замечание 13.5. Интеграл с переменным верхним пределом часто используется для определения новых функций. Мы уже отмечали в лекции 2 (пункт 2.5), что первообразные

13.2.Формула Ньютона Лейбница

Поставим теперь следующую задачу: зная одну из первообразных F (x) функции f(x) на [a; b] вычислить определенный интеграл от функции f(x), или, что тоже самое, по известному неопределенному интегралу найти определенный интеграл.

Теорема 13.2.1 (Основная теорема интегрального исчисления) . Пусть функция f непрерывна на отрезке [a; b] и пусть функция является какой-либо ее первообразной на этом отрезке, тогда

3Лекция 11-12, пункт 11.1, свойство 2.

4Мы установили факт, о котором упоминали еще в первой лекции этого семестра (конец пункта 1.2).

3

Доказательство. Из результатов предыдущего пункта следует, что непрерывная на отрезке [a; b] функция f имеет на этом отрезке первообразную, например

Пусть (x) любая другая первообразная функции f на том же отрезке [a; b]. Так как две первообразные отличаются друг от друга постоянным слагаемым, то получаем

равенство

x

Z

f(t) dt = (x) + C; C 2 R:

a

Подставим в это равенство значение x = a:

a

Z

f(t) dt = (a) + C ) (a) + C = 0 ) C = (a);

f(t) dt = (x) (a) 8 x 2 [a; b]:

a

b

R

Полагая здесь x = b, получаем f(t) dt = (b) (a), что то же самое, что и (13.5).

a

Формула Ньтона Лейбница дает правило вычисления определенного интеграла: зна- чение определенного интеграла на отрезке от непрерывной функции f(x) равно разности

значений любой ее первообразной в точке верхнего и нижнего пределов интегрирования. Разность (b) (a) в правой части равенства (13.5) обычно для краткости обозначают

следующим образом:

b

(b) (a) = (x) ;

a

тогда формула Ньютона Лейбница принимает вид:

b

Z

b

f(x) dx = (x) = (b) (a):

a

a

Формула Ньютона Лейбница позволяет вычислять определенный интеграл не по

определению (т. е. вычисляя предел интегральных сумм), а сводит вычисление определенного интеграла к задаче нахождения неопределенного интеграла.

4