Лекция 18. Классы квадрируемых фигуры

18.1.Площадь криволинейной трапеции

К р и в о л и н е й н о й т р а п е ц и е й называется фигура, ограниченная графиком заданной на отрезке [a; b] непрерывной и неотрицательной функции f(x), перпендикулярными к оси Ox прямыми x = a, x = b и отрезком оси Ox между точками a и b (рис. 1):

= f(x; y) : a x b; 0 y f(x)g:

Рис. 1: Криволинейная трапеция с вписанным и описанным многоугольниками.

Теорема 18.1.1. Криволинейная трапеция представляет собой квадрируемую фигуру , площадь S = j j которой вычисляется по формуле

Доказательство. Непрерывная на отрезке [a; b] функция f(x) интегрируема, поэтому для любого положительного числа " можно указать такое разбиение отрезка [a; b], для которого разность между верхней суммой Дарбу S и нижней суммой Дарбу s будет меньше ". Но S и s равны соответственно jQj и jP j, где jQj и jP j площади многоугольников, первый из которых содержит криволинейную трапецию , а второй содержится в криволинейной трапеции (на рис. 1 изображены также и указанные многоугольники). Таким образом, jQj jP j < ", и в силу теоремы 17.2.1 криволинейная трапеция квадрируема. Поскольку для любой интегрируемой функции предел при стремлении диаметра разбие-

Замечание 18.1. Если функция f(x) непрерывна и неположительна на отрезке [a; b], то

b

R

значение интеграла f(x) dx равно взятой с отрицательным знаком площади криволи-

a

нейной трапеции, ограниченной графиком функции jf(x)j, перпендикулярными к оси Ox прямыми x = a, x = b и отрезком оси Ox между точками a и b (рис. 2).

b

R

Поэтому если f(x) меняет знак, то f(x) dx равен сумме взятых с определенным зна-

a

ком площадей криволинейных трапеций, расположенных выше и ниже оси Ox, причем площади первых берутся со знаком плюс, а вторых со знаком минус (рис. 3).

Некоторые случаи расположения плоской фигуры и соответствующие формулы площади представлены на рисунке (рис. 4).

1

Рис. 2: Площадь фигуры = f(x; y) : a x b; f(x) y 0g.

Рис. 3: Площадь, ограниченная прямыми x = a; x = b; y = 0 и знакопеременной y = f(x).

Рис. 4: Плоские фигуры и соответствующие формулы площади.

2

Замечание 18.2. Нетрудно догадаться, что площадь фигуры

= f(x; y) : 0 x g(y); c y dg;

изображенной на рис. 5, можно вычислить по формуле

c

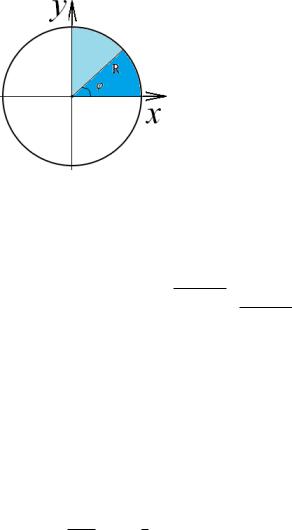
Пример 18.1. Вычислить площадь фигуры, ограниченной кривой в декартовых координатах: x2 + y2 = R2 (ðèñ. 6).

Рис. 6: Круг с границей x2 + y2 = R2.

Очевидно, что это круг с центром в начале координат и радиусом R. Площадь его, известная из школьной программы, равна R2. Убедимся в этом, вычислив искомую пло-

щадь с помощью формулы (18.1).

Окружность x2 + y2 = R2 симметрична относительно координатных осей. Ее часть, p

лежащая в первой четверти, задается функцией y = R2 x2p, 0 x R. Вычислим площадь части круга, ограниченную графиком функции y = R2 x2, 0 x R è

координатными осями (равную, очевидно, 1/4 площади S всего круга):

Таким образом, площадь круга S = a2.

Замечание 18.3. Зная площадь круга, легко определить площадь кругового сектора с центральным углом, величина которого ' выражена в радианах (рис. 6):

Sêðóã.ñåêò. = R2 ' = 1R2':

2 2

18.2.Площадь криволинейного сектора

Пусть кривая L задана в полярной системе координат уравнением r = r('), ' (рис. 7), причем функция r(') непрерывна и неотрицательна на отрезке [ ; ].

Назовем к р и в о л и н е й н ы м с е к т о р о м плоскую фигуру , ограниченную кривой r(') и двумя лучами, составляющими с полярной осью углы и :

= f(r; ') : 0 r r('); ' g:

Åñëè r(') = const, òî ýòî ê ð ó ã î â î é ñ å ê ò î ð.

3

Рис. 7: Площадь криволинейного сектора.

Теорема 18.2.1. Криволинейный сектор представляет собой квадрируемую фигуру j j, площадь S = j j которой может быть вычислена по формуле

Доказательство. Рассмотрим разбиение промежутка [ ; ] точками

= '0 < '1 < : : : < 'i 1 < 'i < : : : < 'n =

èдля каждого частичного промежутка ['i 1; 'i] построим круговые секторы, радиусы

Обратим внимание на то, что первая из этих сумм является нижней суммой Дарбу s а

вторая верхней суммой Дарбу S функции 12r2(') на промежутке [ ; ] для указанного разбиения этого промежутка. Так как непрерывная на [ ; ] функция 12r2(') интегрируема

на этом промежутке, то для любого " > 0 найдется разбиение, для которого разность S s = jBj jAj меньше ".

Так как A и B две квадрируемые фигуры, первая из которых содержится в криволинейном секторе , а вторая содержит то в силу теоремы 17.2.6 криволинейный сектор

квадрируем.

Справедливость для его площади формулы (18.3) вытекает из того, что эта площадь заключена между s = jAj и S = jBj, а обе суммы s и S стремятся к интегралу, стоящему

в правой части (18.3), при стремлении диаметра разбиения к нулю.

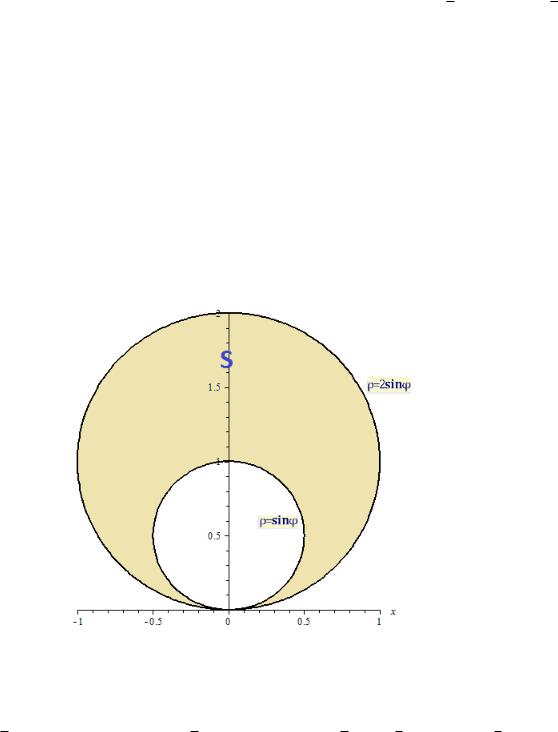
Пример 18.2. Найти площадь фигуры, ограниченной линиями, заданными в полярных координатах:

Используя связь декартовых и полярных координат x = r cos ', y = r sin ' нетрудно

4

заданная в полярных координатах, есть окружность с центром в точке (0; a2) и радиусом a2. Умножив обе части уравнения (18.5) на r, получим r2 = ar sin '. Учтем, что r2 = x2 + y2,

r sin ' = y: Тогда уравнение имеет следующий вид в декартовых координатах:

x2 + y2 = ay:

Приведем это уравнение к уравнению (x x0)2 + (y y0)2 = R2 окружности радиуса R с центром в точке (x0; y0). Для этого перенесем все члены уравнения в левую часть и сгруппируем слагаемые, содержащие y, выделив полный квадрат:

Фигура, ограниченная окружностями (18.4), изображена на рис. 8.

Рис. 8: Фигура, ограниченная окружностями r = sin ', r = 2 sin '.

Вычислим ее площадь:

18.3.Площадь фигуры с параметрически заданной границей

Лемма 18.3.1. Если криволинейная трапеция (рис. 1) ограничена графиком функции, заданной уравнениями в параметрической форме

x = x(t); y = y(t);

5

ãäå t0 t T , осью Ox и прямыми x = a, x = b, причем x(t0) = a, x(T ) = b, то ее площадь при y(t) 0 вычисляется по формуле

Доказательство. Формула (18.6) получается из формулы (18.1) с помощью перехода к переменной t: x = x(t), y = y(t), dx = x0(t)dt. Пределы интегрирования определяются из

равенств x(t0) = a, x(T ) = b.

y y

где x(t) и y(t) непрерывно дифференцируемы на [t0; T ], причем x(t0) = tg , x(T ) = tg , то его площадь вычисляется по формуле

Доказательство. Используя связь декартовых и полярных координат x(t) = r cos '; y(t) = r sin ';

перейдем в интеграле (18.3) к переменной t: r2 = x2(t) + y2(t), ' = arctg xy + C (C зависит от четверти, в которой расположена точка),

Пределы интегрирования определяются из равенств xy (t0) = tg , xy (T ) = tg . Подставив все это в (18.3), получим (18.7).

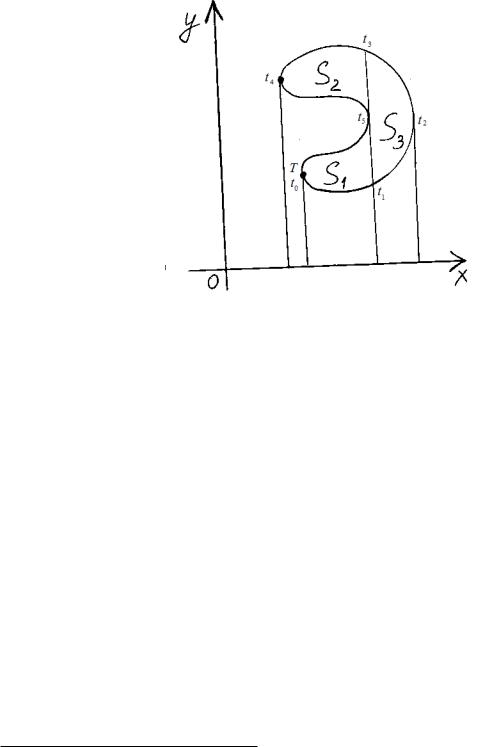
Теорема 18.3.3. Пусть граница @ плоской фигуры простая замкнутая кривая (рис. 9), заданная параметрически уравнениями:

x = x(t); y = y(t); t0 t T;

где x(t) и y(t) непрерывно дифференцируемы на [t0; T ], причем точка (x(t); y(t)) при изменении t от t0 до T пробегает границу @ так, что фигура остается слева от движущейся точки. Тогда фигура квадрируема и ее площадь S = j j может быть вычислена по любой из следующих формул:

6

Рис. 9: Фигура с гладкой границей.

Доказательство. Согласно теореме 15.5.1 граница @ фигуры является спрямляемой кривой, поэтому фигура квадрируема. Это следует из достаточного условия

квадрируемости1.

Разбив фигуру на части как указано на рис. 9, вычислим площадь каждой, используя формулу (18.6):

ZZ

ZZ

ZZ

Сложив вс¼, используя свойство определенного интеграла

ba

ZZ

f(x) dx = f(x) dx

ab

1Теорема 17.2.5

7

и свойство аддитивности по промежутку интегрирования получим формулу (18.8):

ZZ

Д/З: Аналогично, разбивая область прямыми, параллельными оси Ox, и используя формулу (18.2), осуществив в ней переход к переменной t: y = y(t), x = x(t), dy = y0(t)dt,

получите формулу (18.9).

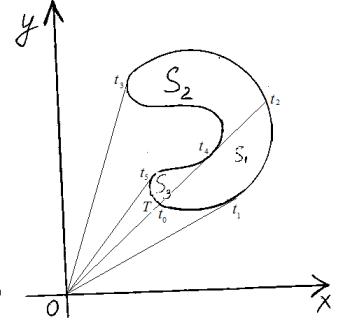
Формулу (18.10) докажем, используя лемму 18.3.2 и разбивая фигуру на части с помощью лучей, выходящих из начала координат, как это сделано на рис. 10.

Рис. 10: Разбиение фигуры на части с помощью лучей, выходящих из начала координат.

Площадь каждой части вычислим, используя формулу (18.7):

Сложив вс¼, используя свойство определенного интеграла

ba

ZZ

f(x) dx = f(x) dx

ab

èсвойство аддитивности по промежутку интегрирования получим формулу (18.10).

8

Замечание 18.1. Формула (18.10) бывает особенно эффективна, если в параметризации кривой участвуют тригонометрические функции.

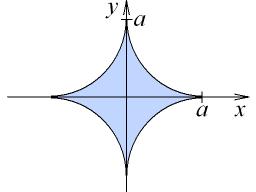
Пример 18.3 (Площадь внутри астроиды.). Астроиду можно параметризовать следу-

Рис. 11: Площадь внутри астроиды.

9