Лекция 17. Площадь плоской квадрируемой фигуры

17.1.Понятие квадрируемости плоской фигуры

П л о с к о й ф и г у р о й будем называть любое ограниченное множество точек плос-

кости.

Множество называется о г р а н и ч е н н ы м, если существует круг, содержащий все точки этого множества.

Для приближенного вычисления площади на практике используют, например, палеткупрозрачную пластину или лист бумаги, на который нанесена квадратная сетка. Накла-

дывая ее на фигуру, подсчитывают число квадратов, содержащихся в фигуре. Это число, умноженное на площадь одного квадрата, равно приближенному значению площади фигуры с недостатком. Чтобы получить приближенное значение площади фигуры с избытком, считают все квадраты сетки, имеющие с фигурой общие точки. Взяв среднее арифмети-

Рис. 1: Приближенное измерение площади с помощью палетки.

ческое между этими значениями, получим приближенное значение площади этой фигуры. Чем мельче квадратная сетка палетки, тем более точный результат можно получить.

Встает вопрос: для каких плоских фигур можно обобщить этот метод отыскания площади? Естественно, надо определить, что такое площадь и квадрируемая фигура.

Для введения понятия площади плоской фигуры будем отправляться от специального частного вида плоских фигур, так называемых многоугольников.

Многоугольником будем называть часть плоскости, ограниченную простой замкнутой ломаной линией, т. е. замкнутой кривой без самопересечений, состоящей из конечного числа прямолинейных звеньев (отрезков), соединенных таким образом, что начало следующего отрезка совпадает с концом предыдущего, начало первого отрезка совпадает с концом последнего. Точки этой ломаной являются граничными 1 точками многоугольника. Совокупность всех граничных точек множества называется г р а н и ц е й этого множества.

Площадь любого многоугольника можно вычислить, разбив его на непересекающиеся треугольники (без общих внутренних точек). Из курса средней школы известны следующие формулы вычисления площади треугольника.

1. Формула площади треугольника по стороне и высоте. Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к

1Напомним, что точку M называют граничной точкой множества A, если в любой -окрестности точ- ки M найдутся как точки, принадлежащие множеству A, так и не принадлежащие A.

1

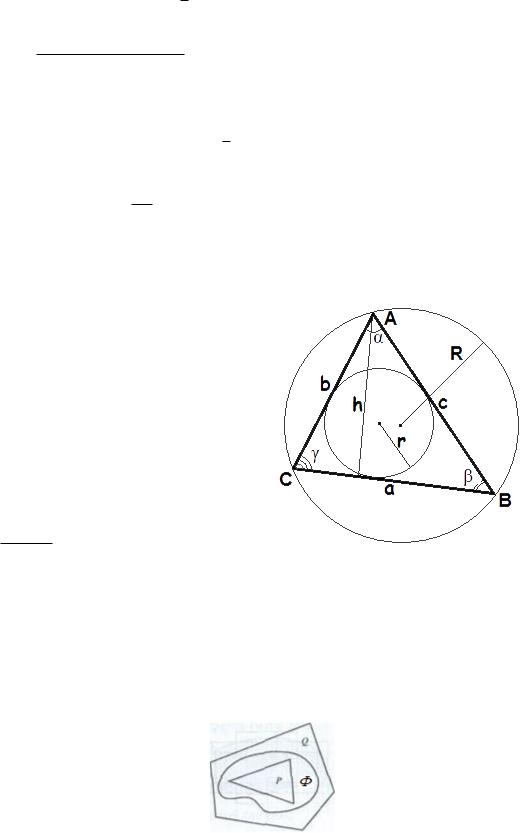
этой стороне высоты: S = 12ah:

2. Формула площади треугольника по трем сторонам (Формула Герона):

p

S = p(p a)(p b)(p c):

3. Формула площади треугольника по двум сторонам и углу между ними.

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними: S = 12ab sin :

4.Формула площади треугольника по трем сторонам и радиусу описанной окружности: S = abc4R :

5.Формула площади треугольника по трем сторонам и радиусу вписанной

окружности. Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности: S = pr:

Здесь S площадь треугольника,

a, b, c длины сторон треугольника,

h высота треугольника,

угол между сторонами a и b,

r радиус вписанной окружности,

R радиус описанной окружности,

p= a+b +c полупериметр треугольника.

2

Будем говорить, что многоугольник P в п и с а н в фигуру , если каждая точка многоугольника P принадлежит фигуре . Если все точки плоской фигуры принадлежат некоторому многоугольнику Q, то будем говорить, что указанный многоугольник Q о п и - с а н вокруг фигуры . На рисунке 2 показано, что многоугольник Q содержит фигуру ,

ò.е. Q описанный многоугольник для фигуры , а многоугольник P содержится в ,

ò.е. P вписанный многоугольник для фигуры . На теоретико-множественном языке это означает, что P F Q.

Рис. 2: Вписанный и описанный мноугольники для плоской фигуры .

Обозначим площади вписанного и описанного многоугольников соответственно jP j и jQj. Ясно, что площадь любого вписанного в фигуру многоугольника не больше площади

2

Следовательно, fjP jg множество площадей вписанных в плоскую фигуру многоугольников ограничено сверху (площадью любого описанного вокруг фигуры многоугольника), а fjQjg множество площадей описанных вокруг фигуры многоугольников ограничено снизу (площадью любого вписанного в фигуру многоугольника). Как из-

вестно2, всякое непустое, ограниченное сверху (снизу) множество, имеет точную верхнюю (точную нижнюю) грань. Обозначим s = supfjP jg и назовем это число в н у т р е н н е й

ïо щ а д ь ю фигуры ; число S = inf fjQjg назовем соответственно в н е ш н е й п л о -

Q

щ а д ь ю фигуры .

Утверждение 17.1.1. Внутренняя площадь фигуры не больше внешней площади:

s = supfjP jg inf fjQjg = S:

P Q

Доказательство. Так как для любых вписанных и описанных многоугольников P и Q, соответствующих фигуре , справедливо неравенство (17.1), то любая площадь jQj является верхней гранью множества fjP jg. Тогда

так как точная верхняя грань множества это наименьшая из его верхних граней. Из

соотношений (17.2) следует, что s нижняя грань множества fjQjg и s inf fjQjg, òàê

Q

как точная нижняя грань множества это наибольшая из его нижних граней. Таким образом, утверждение доказано: s S.

Определение 17.1 (Понятие площади по Жордану3). Плоская фигура называется к в а д р и р у е м о й (или имеющей площадь), если внешняя площадь S этой фигуры совпадает с ее внутренней площадью s. При этом число S = S = s называется площадью фигуры .

Пример 17.1 (Неквадрируемая фигура). Рассмотрим плоскую фигуру:

где D(x) функция Дирихле: D(x) = 1, если x число рациональное, и D(x) = 0, если xчисло иррациональное.

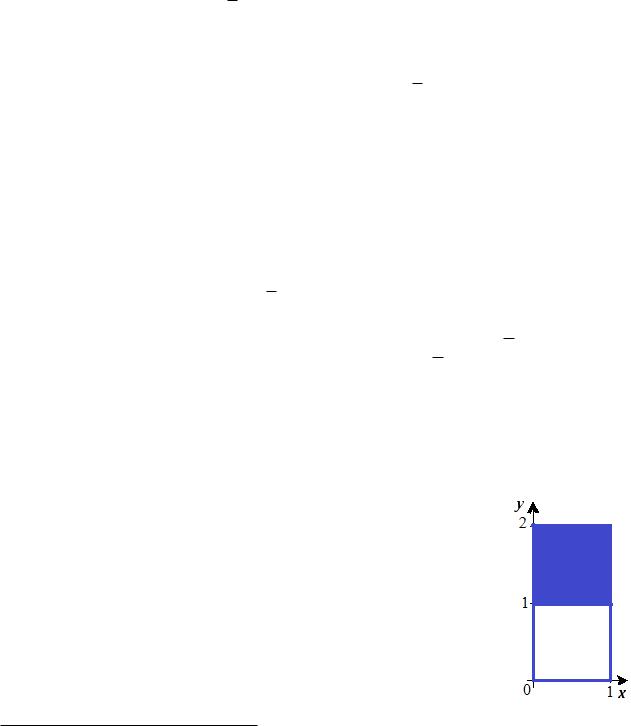
Как видно из (17.3) у всех точек фигуры c рациональной абсциссой x ордината y 2 [0; 2], в то же время все точки фигуры c иррациональной абсциссой x имеют ординату y 2 [0; 1]. Следовательно, точки из множества = f(x; y) : 0 x 1; 1 y 2g являются

граничными. Все множество граничных точек фигуры (17.3) отме- чено синим цветом на рисунке. Среди этих точек есть принадлежащие (те, у которых x рациональное) и не принадлежащие

(те, у которых x иррациональное); граница y = 0, очевидно, принадлежит .

Нетрудно видеть, что максимальная площадь вписанного в многоугольника равна 1,

2Семестр I, лекция 3.

3Камилл Жордан французский математик (1838 1922).

3

и минимальная площадь описанного вокруг многоугольника равна 2, т. е. s( ) = 1,

S( ) = 2. Согласно определению 17.1 фигура (17.3) не является квадрируемой.

17.2.Критерии квадрируемости

Теорема 17.2.1. Для того чтобы плоская фигура была квадрируемой, необходимо и достаточно, чтобы для любого положительного числа " можно было указать такой описанный вокруг фигуры многоугольник Q и такой вписанный в фигуру многоугольник P , разность jQj jP j площадей которых была бы меньше ": jQj jP j < ".

Доказательство. Необходимость. Пусть фигура квадрируема, т. е. s = S = S. Òàê êàê

то согласно определению точной верхней грани множества fjP jg для любого числа " > 0 можно указать такой вписанный в фигуру многоугольник P , площадь которого отли- чается от s меньше чем на "=2:

8 " > 0 9 P : jP j > s 2";

соответственно, согласно определению точной нижней грани множества fjQjg для того же числа " > 0 можно указать такой описанный вокруг фигуры многоугольник Q, площадь которого отличается от S меньше чем на "=2:

9 Q : jQj < S + 2":

Складывая полученные неравенства, найдем (с учетом равенства s = S), ÷òî

8 " > 0 9 P; Q; P ; Q : jQj jP j < S s + " = ":

Достаточность. Пусть 8 " > 0 9 P; Q; P ; Q : jQj jP j < ":

С учетом того, что jP j s S jQj, имеем

8 " > 0 0 S s jQj jP j < ":

В силу произвольности " это означает, что S s = 0. Таким образом, фигура квадрируема. Теорема доказана.

Определение 17.2. Будем говорить, что граница @ плоской фигуры и м е е т п л о - щ а д ь , р а в н у ю н у л ю , если для любого положительного " можно указать такой описанный вокруг фигуры многоугольник Q и такой вписанный в фигуру многоугольник P , разность площадей которых меньше ": jQj jP j < ".

При этом теорему 17.2.1 можно сформулировать следующим образом.

Теорема 17.2.2. Для того чтобы плоская фигура была квадрируемой, необходимо и достаточно, чтобы е¼ граница @ имела площадь, равную нулю.

Если Q многоугольник, взятый вместе с границей и содержащий плоскую фигуру , а P многоугольник, содержащийся в фигуре , взятый без границы, то разность множеств Q n P представляет собой многоугольную фигуру, взятую вместе с границей и содержащую все точки границы @ фигуры . В силу свойства аддитивности площади многоугоугольника справедливо равенство jQ nP j = jQj jP j, тогда теорему 17.2.1 можно также сформулировать следующим образом.

4

Теорема 17.2.3. Для того чтобы плоская фигура была квадрируемой, необходимо и достаточно, чтобы е¼ граница @ могла быть помещена в многоугольную фигуру сколь угодно малой площади.

Определение 17.3. Множество точек плоскости назовем м н о ж е с т в о м п л о щ а д и н у л ь, если оно содержится в могоугольной фигуре сколь угодно малой площади.

Лемма 17.2.4. Всякая спрямляемая кривая имеет площадь нуль.

Доказательство. Пусть L спрямляемая кривая, а ` ее длина. Разобьем эту кривую с помощью n+1 точек на части, длина каждой из которых равна `=n. (Возможность такого разбиения не вызывает сомнений.) Примем каждую из этих n + 1 точек за центр квадрата со стороной 2`=n. Объединение этих квадратов представляет собой многоугольную фигуру, описанную вокруг кривой L, а площадь этой многоугольной фигуры не превосходит

4`2

но, а n можно выбирать произвольно большим, то число n2 (n + 1) может быть сделано меньшим любого наперед заданного числа " > 0. Следовательно, кривую L действительно

можно заключить внутрь многоугольной фигуры сколь угодно малой площади. Лемма доказана.

Из этой леммы и теоремы 17.2.2 вытекает следующий достаточный признак квадрируемости плоской фигуры.

Теорема 17.2.5. Всякая плоская фигура, граница которой состоит из одной или нескольких спрямляемых кривых, квадрируема.

Теорема 17.2.1 допускает простое, но важное обобщение: в ее формулировке вместо описанного и вписанного многоугольников Q и P можно взять произвольные описанную

и вписанную к в а д р и р у е м ы е плоские фигуры Q è P . Именно справедлива теорема.

Теорема 17.2.6. Для квадрируемости плоской фигуры необходимо и достаточно, чтобы для любого " > 0 нашлись такие содержащая квадрируемая плоская фигура Q è такая содержащаяся в квадрируемая плоская фигура P , для которых разность пло- щадей меньше ":

j Qj j P j < ":

Доказательство. Необходимость доказательства не требует, ибо существующие при этом описанный и вписанный многоугольники Q и P являются квадрируемыми.

Достаточность. Фиксируем произвольное " и построим по нему квадрируемые плос-

кие фигуры Q è P , первая из которых содержит , а вторая содержится в , такие, что

Òàê êàê Q è P квадрируемые плоские фигуры, то найдется многоугольник Q, содержащий Q, и многоугольник P , содержащийся в P , такие, что

Из двух последних неравенств и из (17.4) вытекает, что jQj jP j < ":

5

Но тогда, поскольку многоугольник Q содержит , а многоугольник P содержится в , фигура квадрируема в силу теоремы 17.2.1.

Теорема 17.2.3 также допускает аналогичное обобщение.

Теорема 17.2.7. Для того чтобы плоская фигура была квадрируемой, необходимо и достаточно, чтобы е¼ граница @ могла быть помещена в плоскую фигуру сколь угодно малой площади.

6