практикаинтегралы / Занятие 10 Интегрирование дифференциального бинома

Занятие 10

1.5.10. Интегрирование дифференциального бинома

Интеграл от дифференциального бинома

где m, n и p -рациональные числа, может быть приведен к интегрированию рациональных функций лишь в следующих трёх случаях ( теорема Чебышева ):

Случай 1. Пусть p - целое. Тогда полагая , где N - общий знаменатель дробей m и n.

Случай 2. Пусть - целое. Тогда полагаем , где N - знаменатель дроби p.

Случай 3. Пусть - целое. Тогда применяем подстановку , где N - знаменатель дроби p.

Если , то эти случаи эквивалентны следующим:

1) p -целое; 2) m - целое; 3) m+n - целое.

№1985 = перепишем подинтегральное выражение в виде дифференциального бинома = теперь понятно, что . Убедимся, что этот дифференциальный бином принадлежит к одному из трех указанных случаев. 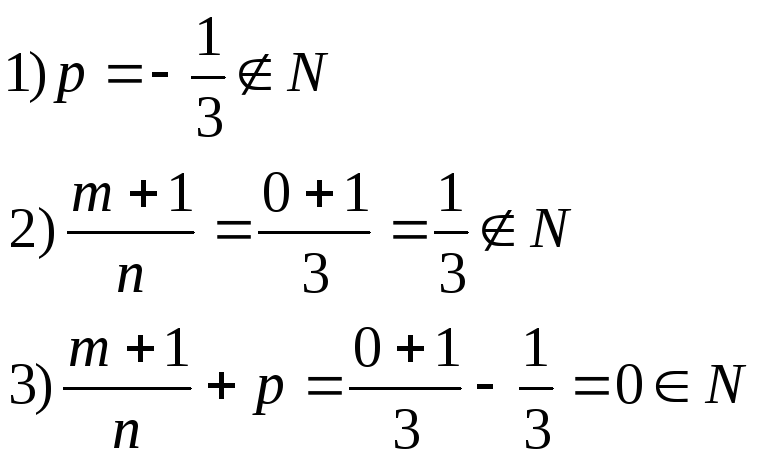Проверка показала, что подинтегральную функцию приведет к рациональному виду подстановка . Действительно = = = , и задача свелась к нахождению интеграла от правильной рациональной дроби, которую надо представить в виде суммы элементарных дробей. = = =  Поиск интегралов от этих элементарных дробей – задача уже известная. = = + = = = =

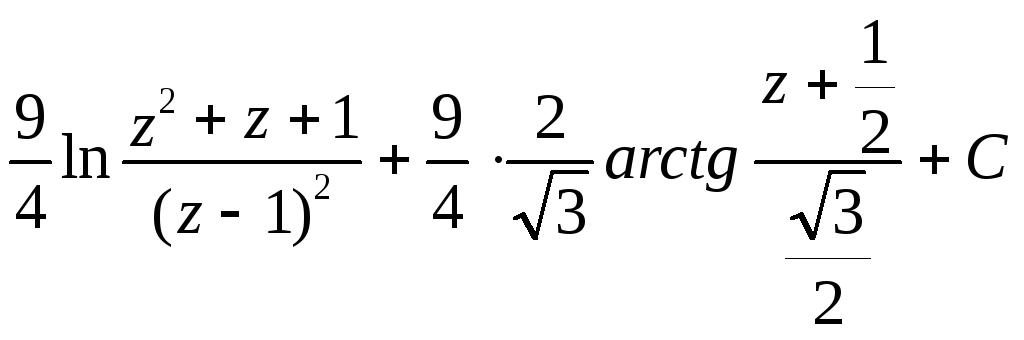Аналогично решаются №№ 1981, 1983, 1989.

Домашнее задание №№ 1982, 1986, 1988.