2.4.2. Максимальный (критический) момент

Для определения максимального момента необходимо взять первую производную от М по S и приравнять к нулю

.

Определим из полученного выражения критическое скольжение - S_крсоответствующего максимальному моменту

, (1)

обычно , то,

критическое скольжение определяется соотношением активного сопротивления ротора к суммарному индуктивному сопротивлению обмотки ротора и статора.

Если подставим выражение (1) в общее уравнение момента и сделаем необходимые преобразования, то получим выражение максимального момента.

Знак + ­­­­­­­­­­­­- соответствует двигательному режиму

Знак - - соответствует генераторному режиму

При генераторном режиме

Из выражения М_крвидно, что величина максимального момента не зависит от активного сопротивления роторной цепи, но сильно оно влияет на его расположение. Если сопротивление роторной цепи увеличивать , то увеличивается S_кри кривая момента смещается вправо

,

Как видно из кривых, чем больше активное сопротивление в роторной цепи, тем больше пусковой момент и меньше пусковой ток. Это ценное свойство используется в двигателях с фазным ротором.

2.4.3. Расчетная формула момента

Расчетная формула момента показывает, что момент асинхронного двигателя пропорционален потоку и активной составляющей тока ротора.

Запишем известное выражение момента

для вывода расчетной формулы используем нижнюю часть векторной диаграммы асинхронного двигателя

,,,

тогда

тогда , т.е. момент зависит от потока и активной составляющей тока ротора.

2.4.4. Влияние высших гармоник магнитного поля на работу асинхронной машины

Высшие гармоники магнитного поля возникают:

a) вследствие ступенчатого распределения намагничивающей силы статора и ротора;

б) зубчатого строения поверхности статора и ротора;

в) неравномерным насыщением магнитной цепи машины.

Вращающие моменты, обусловленные высшими гармониками поля, могут быть разбиты на три группы:

1. Асинхронные

2. Синхронные

3. Вибрационные

1. Асинхронные моменты, cозданные высшими гармониками магнитного поля.

Гармонические магнитного поля, имеющие пространственный период меньше 2 могут возникать в асинхронной машине как в результате несинусоидальности намагничивающих сил, так и вследствие зубчатости воздушного зазора. Высшие гармоники поля передвигаются в направлении движения ротора и создаются током статора. Это поле наводит в обмотке ротора ЭДС и ток соответствующей частоты, который создает магнитное поле, передвигающееся по поверхности ротора, и вращается в воздушном зазоре синхронно с полем статора. Магнитные поля статора и ротора будут иметь одинаковые пространственные периоды и создадут результирующее поле. Это поле взаимодействуя с током в роторе создает вращающий момент, который по его природе следует рассматривать как асинхронный. Высшие гармоники поля создают соответствующие моменты, которые искажают момент от первой гармоники поля.

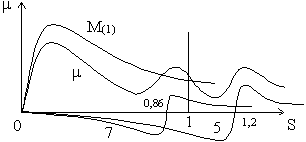
Рассмотрим влияние 5 и 7 гармоники поля на момент от первой гармоники поля

,

седьмая гармоника поля вращается в сторону первой гармоники

,

пятая гармоника поля вращается против первой гармоники.

Асинхронные моменты, обусловленные высшими гармониками поля могут быть ослабленны за счет рационального размещения зубцов в слое обмоток статора и ротора (Z₁и Z₂). Обеспечение синусоидальности намагничивающей силы и максимального снижения зубцовых гармоник.

2. Cинхронные моменты от высших гармоник магнитного поля.

Не все высшие гармонические магнитного поля, созданные статором и ротором сцепляются с обеими обмотками и образуют асинхронные вращающие моменты. Это особенно характерно для зубцовых высших гармоник. При определенных скоростях вращения ротора отдельные гармонические зубцового поля статора могут двигаться синхронно с соответствующими гармоническими зубцового поля статора. Под действием магнитных сил в этом случае возникают механические воздействия между статором и ротором и создаются синхронные моменты для какого-то одного значения скольжения. При этом пространственный период основной зубцовой гармоники статора и ротора должен быть одинаков. То есть

т.е. при

синхронные моменты будут сильно проявляться.

Синхронные моменты могут быть ослаблены за счет скоса и правильного выбора соотношений зубцов статора и ротора.

3. Вибрационные силы и моменты

Зубцовые и другие магнитные поля статора ротора, образующие синхронные моменты, проявляющиеся не только при взаимном синхронном их вращении, но и при любых других скоростях вращения. В этом случае они образуют периодически меняющиеся вращающиеся моменты, которые в течение одного полупериода направлены в сторону вращения ротора, а в течении другого полупериода в обратном направлении. Такие периодически меняющиеся моменты могут создавать вибрации ротора и статора, которые становятся особенно заметными при наличии резонансных явлений. При неблагоприятных соотношениях зубцов статора и ротора могут возникнуть не только тангенциальные, но так же и радиальные магнитные силы притяжения, действующие на статор и ротор и перемещающиеся вдоль окружности воздушного зазора при вращении ротора, эти силы вызывают вибрацию машины.

Анализ этих процессов показывает, что вибрационные силы и моменты проявляются особенно сильно, если

2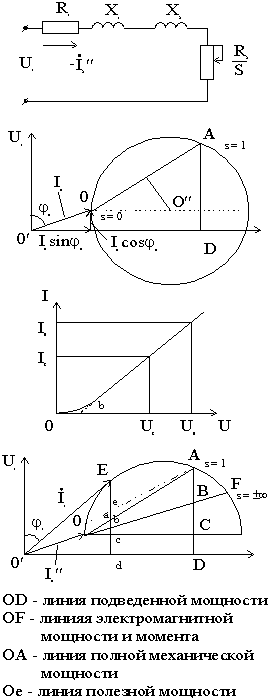.5. Круговая диаграмма асинхронной машины

Рабочие и другие характеристики асинхронного двигателя, определяющие рабочие свойства машины, могут быть получены:

1. Путем непосредственной нагрузки.

2. Расчетным путем (определение параметров и расчет характеристик).

3. Косвенный метод (по данным опыта холостого хода и короткого замыкания). Используя данные опыта холостого хода и короткого замыкания можно построить упрощенную круговую диаграмму, а из нее получить данные для построения рабочих характеристик.

Из Г–образной схемы замещения

,

Обозначим в рабочей ветви

,,,

тогда

ток -

Геометрическим местом тока является окружность.

Построение круга диаграммы.

Из опыта холостого хода для U_Ннаходим

Р₀ иI₀,I₀= , ,

и определяем ,

а по ним строится вектор тока хх – I₀, задавшись масштабом токаm_I(A/см)

Для построения точки А, где S= 1 приводим токI_к, мощность Р_киCos_кк номинальному напряжениюI_пU_н. Из рис. 2

, откуда

,,

Откладываем отрезок ,получаем точку А. Соединив точку А с О получим хорду окружности. Опуская перпендикуляр из середины хорды до линииполучим центр окружности.

Построение линии OF. Определение точки В.

,,r₁- известно

откуда отрезок .

Получим точку В. Соединив точку О с В и продлив до окружности получим точку F где S=. Мощность, т.е.

,

Задавшись m_I, определим масштаб мощности

Тогда мощность

,,

Как получить данные из круговой диаграммы для построения рабочих характеристик?

P₁, I₁, , Cos₁, S, n = f(P₂)