3.2. Кинетическое условие химического равновесия. Константа равновесия

Пусть в системе протекает простая обратимая реакция

_AA + _BB  _DD + _EE.

Скорости прямой и обратной реакции определяются законом действующих масс: прямая реакция, обратная.

Рассмотрим изменение концентраций реагентов и соответственно скоростей реакций во времени. Пусть в момент времени t = 0 в реакционном объеме находятся только исходные вещества A и B и их концентрации равны С_A0 и С_B0. В ходе реакции эти вещества будут расходоваться и соответственно будет уменьшаться скорость прямой реакции.

Поскольку в начальный момент времени (t=0) веществ D и E в реакционном объеме нет, то скорость обратной реакции равна нулю. В ходе реакции эти вещества будут образовываться, их концентрация будет увеличиваться и соответственно будет увеличиваться скорость обратной реакции.

В определенный момент времени скорость прямой реакции станет равной скорости обратной реакции (). Это значит, что число молекул веществA и B, израсходованных в единицу времени в результате прямой реакции, будет равно числу этих же молекул, образовавшихся в результате обратной реакции. И наоборот, число молекул веществ D и E, образовавшихся в единицу времени в результате прямой реакции, будет равно числу этих же молекул, израсходованных в результате обратной реакции. Поскольку концентрации реагирующих веществ (исходных веществ и продуктов реакции) не изменяются во времени при условии постоянства температуры и давления в реакционной смеси, то система находится в состоянии равновесия. Концентрации реагентов соответствуют равновесным. Отметим, что это состояние является динамическим равновесием, так как в системе протекают химические реакции.

Поскольку в состоянии равновесия скорости прямой и обратной реакции равны и соответственно=, то можно написать:

.

Таким образом, состояние равновесия характеризуется постоянной величиной – константой равновесия (К), которая равна отношению констант скоростей прямой и обратной реакций. С другой стороны, она равна отношению произведения равновесных концентраций продуктов к произведению равновесных концентраций исходных веществ, взятых в степенях, равных соответствующим стехиометрическим коэффициентам. Величина константы равновесия зависит от природы реагирующих веществ и температуры и не зависит от концентрации реагирующих веществ.

Константа равновесия определяет соотношение концентраций всех реагирующих веществ в состоянии равновесия – соотношение равновесных концентраций (С_iр). Константа равновесия представляет собой постоянную величину для данной химической реакции при определенной температуре и не зависит от первоначального состава реагирующей смеси. Зная исходную концентрацию реагентов, уравнение химической реакции и константу равновесия, можно определить равновесную концентрацию всех веществ.

Пример. В системе при температуре 700 К протекает гомогенная обратимая реакция взаимодействия водорода и газообразного иода: H₂ + I₂  2HI. Порядок реакции по каждому компоненту совпадает со стехиометрическими коэффициентами. Константа равновесия реакции при данной температуре К=55,56. Константа скорости прямой реакции H₂ + I₂  2HI равна: =0,1 лмольс. Константа скорости обратной реакции 2HI  H₂ + I₂ равна: = 0,0018 л мольс.

Пусть в момент времени t = 0 начальные концентрации реагирующих веществ равны С_Н20 = С_I20 = 0,01 мольл; С_НI0 = 0. Тогда при t = 0 начальные скорости прямой и обратной реакций в соответствии с кинетическими уравнениями будут соответственно равны:

= С_H2¹С_I2¹ = 0,1 (0,01)¹(0,01)¹ = 10^-5 мольлс,

= С_HI²= 0,0018 (0)² = 0.

На рис. 3.1 приведены зависимости от времени концентраций реагентов и скоростей прямой и обратной реакции. Видно, что изменение скоростей реакций соответствует изменению концентрации реагентов. Начиная с момента t = t_р, концентрации реагентов в системе не меняются и, соответственно, . Система пришла в состояние равновесия.

Рис. 3.1. Изменение концентрации реагирующих веществ и скорости прямой и обратной реакции H₂ + I₂  2 HI во времени (при t = 0 С_Н20 = С_I20 = 0,01 мольл; С_НI0 = 0)

Равновесные концентрации реагентов можно рассчитать, зная их начальные концентрации и константу равновесия. Пусть за время прихода системы в состояние равновесия концентрация водорода изменится на величину x. Тогда в соответствии с уравнением реакции можно написать:

(с_H2)_p = (с_I2)_p = (0,01 – x) мольл, (с_HI)_p = (2 x) мольл,

.

Решение квадратного уравнения относительно x позволяет рассчитать равновесные концентрации реагентов:

(с_H2)_p = (с_I2)_p = 0,00212 мольл, (с_HI)_p = 0,0158 мольл.

В состоянии равновесия скорости прямой и обратной реакций равны:

= 0,1 (0,00212)¹(0,00212)¹ = 4,510^-7 мольлс,

= 0,0018(0,0158)² = 4,510^-7 мольлс.

Рассмотрим константу равновесия сложной реакции. Сложная обратимая реакция протекает через ряд промежуточных элементарных реакций, и химическое равновесие установится, если существуют равновесия в каждой стадии. Это положение получило название принцип микроскопической обратимости или принцип детального равновесия.

Пусть в системе протекает сложная обратимая химическая реакция

_AA + _BB  _DD + _EE,

стадиями которой будут:

1. _AA  _A1A₁ + _A2A₂ ,

2. _ВВ  _В1В₁ + _В2В₂ ,

3. _A1A₁ + _В1В₁  _DD ,

4. _A2A₂+ _В2В₂ _EE ,

где – константы скоростей прямой и обратнойi-й элементарной реакции.

В состоянии равновесия системы каждой элементарной реакции будет соответствовать константа равновесия K_i:

1. =,,

2. =,,

3. =,,

4. =,.

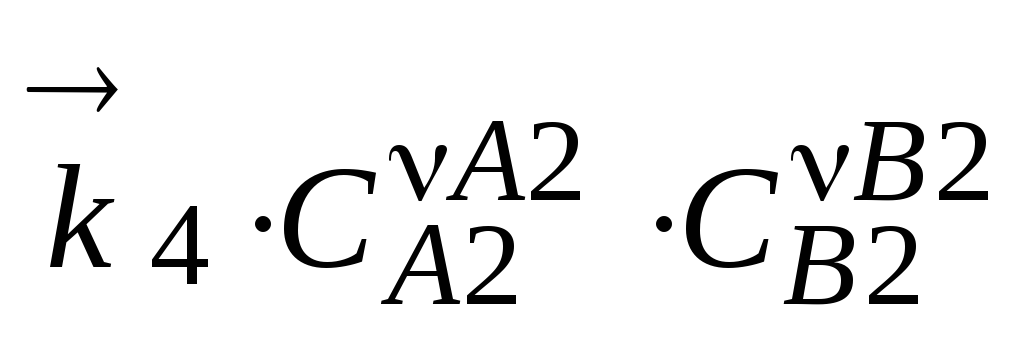Уравнение сложной химической реакции получается сложением всех элементарных реакций. При этом константа равновесия суммарного процесса (К) будет представлять собою произведение констант равновесия каждой элементарной стадии. Очевидно, что концентрации промежуточных продуктов, входящие в выражение констант равновесия отдельных стадий, являются одними и теми же:

,

.

Таким образом, в выражение константы равновесия сложной реакции входят концентрации только исходных веществ и продуктов реакции в степенях, равных их стехиометрическим коэффициентам в уравнении суммарной реакции. Константа равновесия сложной реакции не зависит от промежуточных стадий, т. е. от ее механизма. Поэтому изменение скоростей отдельных промежуточных реакций, например при использовании катализаторов, только ускоряет приход системы в состояние равновесия, но не изменяет величины равновесных концентраций.

Необходимо отметить, что поскольку в кинетические уравнения гетерогенных реакций не включаются концентрации реагентов, находящихся в твердой фазе, то соответственно они не включаются и в константу равновесия.

Пример.

1. Гетерогенная гомофазная реакция взаимодействия твердого углерода с диоксидом углерода: C _тв+ CO_{2 газ}  2CO _газ.

Константа равновесия .

2. Гетерогенная гетерофазная реакция окисления металла: x Me + y/2 O₂  Me_xO_y.

Константа равновесия .

Очевидно, что величина константы равновесия, полученная из кинетического условия, имеет размерность. Она зависит от того, в каких единицах задаются концентрации реагирующих веществ и стехиометрических коэффициентов в уравнении реакции. Для реакции _AA+ _BB  _DD+ _EE константа равновесия может быть выражена следующим образом:

 K_X – концентрации задаются мольными долями реагентов (безразмерная величина):

 K_p [(Па)^] – (для газовых реакций) концентрации задаются парциальными давлениями (Па) реагентов:

 K_C [(моль/л)^] – концентрации задаются молярной концентрацией реагентов (моль/л):

Из термодинамических условий была получена стандартная константа равновесия К⁰, которая рассчитывается из термодинамических характеристик реакции: изменения энергии Гиббса, энтальпии и энтропии в ходе реакции _rG⁰(T), _rH⁰(T); _rS⁰(T). Отметим, что стандартная константа равновесия является безразмерной величиной, так как в ее выражения входят безразмерные концентрации реагентов (см. подразд. 3.1). Поскольку система находится в состоянии равновесия, то и константы равновесия, полученные из кинетических и термодинамических условий, должны быть связаны между собой. Эта связь выражается следующими соотношениями:

, ,,

где  = (_D + n_E) – (n_A + n_B) – изменение числа молей в ходе реакции; р⁰ = 1,01310⁵ Па – стандартное давление; – относительное давление, безразмерное по сущности, но имеющее размерность «физическая атмосфера» (атм).

В какую сторону будет смещаться равновесие при изменении температуры и концентрации взаимодействующих веществ, подробно рассмотрено при анализе термодинамических условий равновесия. С точки зрения кинетических условий смещение равновесия обусловлено изменением соотношения скоростей прямой и обратной реакций при изменении равновесных параметров в соответствии с законом действующих масс и уравнением Аррениуса. Результат влияния изменения равновесных параметров на смещение равновесия с точки зрения кинетики и термодинамики, естественно, будет одинаков.