Управление в ТС. Лабораторные работы / Теория / Лабораторная работа №1 (АФХ)

Примерный график АЧХ представлен на рис. 14.

Выражение для ФЧХ:

.

П

роанализируем его:

- при  = 0 ;

- при , и , .

Примерный график представлен на рис. 15.

Пример 6.

;

,

где , , , .

Прежде всего отметим, что следствием указанного выше правила умножения комплексных чисел являются следующие отношения: , , n - натуральное число.

С учетом этого составим выражение для АЧХ:

.

Проанализируем его:

-

при  = 0 A(0) = k;

- при , , , , ;

- все сомножители в выражении для АЧХ изменяются монотонно.

Примерные графики АЧХ для различных соотношений постоянных времени показаны на рис. 16.

Составим выражение для ФЧХ и проанализируем его:

- при  = 0 (0) = 2^.0 – 0 – 3^.0 = 0;

-

при каждый арктангенс достигает значения , .

Отметим также, что в зависимости от соотношения постоянных времени график  может иметь разный вид. На рис. 17 показаны примерные графики для следующих случаев:

- значение T₁ значительно превышает T₂ и T₃;

- значения постоянных времени примерно одинаковы;

- значение T₁ значительно меньше T₂;

2. Вещественная и мнимая частотные характеристики

Вещественной частотной характеристикой (ВЧХ) называется вещественная часть частотной передаточной функции: .

Мнимой частотной характеристикой (МЧХ) называется мнимая часть частотной передаточной функции: .

Для получения ВЧХ и МЧХ выражение для ЧПФ необходимо преобразовать к виду суммы

.

Основная задача, которую приходится решать при таком преобразовании, состоит в исключении комплексных выражений из знаменателя ЧПФ. Способ решения этой задачи известен из математики – домножение числителя и знаменателя на выражение, комплексно сопряженное к знаменателю.

Комплексно сопряженными являются выражения, отличающиеся знаком мнимой части: и .

Произведение комплексно сопряженных выражений оказывается вещественным:

.

В частном случае для чисто мнимого выражения получим: . Отметим особо следующий результат: j(-j)=1.

Получаемые в результате указанного преобразования выражения для ВЧХ и МЧХ справедливы как для положительных, так и для отрицательных частот. Тем не менее, для контроля правильности построения графиков этих характеристик следует помнить, что ВЧХ U() является четной функцией, а МЧХ V() - нечетной.

Пример 7.

Апериодическое звено 1 порядка.

.

Таким образом, использование указанного выше способа позволило избавиться от комплексного выражения в знаменателе. Осталось разбить полученное выражение на два слагаемых. Первое из них не должно содержать в своем составе символа j, для второго символ j должен быть общим сомножителем:

.

В результате: , .

Проанализируем полученное выражение для ВЧХ и построим её график (рис. 18):

• при  = 0 ;

• при знаменатель стремится к бесконечности, и .

Д

ля МЧХ (рис. 19):

• при  = 0

;

• при T >> 1,

, ;

• при  > 0 V()< 0 .

Пример 8.

, .

В знаменателе содержатся два комплексных сомножителя: (удобнее рассматривать отдельно j) и . Комплексно сопряжёнными для них будут соответственно: - j и .

Выполним преобразование:

;

, .

П

роанализируем полученные выражения и построим их примерные графики (рис. 20 и 21):

• при  = 0 ;

• ;

• при , при ;

• при  > 0 , при  < 0 ;

• ;

• п

  

  ри  > 0 .

3. Амплитудно-фазовая частотная характеристика

Амплитудно-фазовой частотной характеристикой (амплитудно-фазовой характеристикой, АФХ) называется годограф частотной передаточной функции.

Годограф комплексной функции одного вещественного аргумента строится на комплексной плоскости, показанной на рис. 2. Любому значению аргумента на комплексной плоскости соответствует точка. Множество точек, соответствующее плавному изменению аргумента от -  до , образует кривую, которая и называется годографом.

П

усть задана ЧПФ W(j). Для некоторой частоты ₁ (для определенности ₁ > 0) соответствующая точка на комплексной плоскости может быть построена в декартовых координатах (рис. 22) на основе представления ЧПФ в алгебраической форме: W(j₁ ) = U(₁ ) +jV(₁ ), где U(₁) – значение ВЧХ, V(₁) – значение МЧХ на частоте ₁ .

Представление ЧПФ в показательной форме даёт полярные координаты такой точки:

,

где А(_) - значение АЧХ, (_) - значение ФЧХ частоте _.

При плавном изменении частоты от 0 до  множество соответствующих точек образуют кривую, например, как показано на рис. 22.

Для получения второй половины годографа, соответствующей отрицательным частотам, определим положение изображающей точки для  = -_ на основе свойств четности и нечетности частотных характеристик.

ВЧХ является четной функцией, следовательно, при изменении знака аргумента  горизонтальная координата изображающей точки сохраняет свое значение U(-_) = U(_). МЧХ – нечетная функция, следовательно, при изменении знака  изменяется знак вертикальной координаты изображающей точки V(-_) = - V(_).

Таким образом, точки годографа, соответствующие частотам _ и -_, симметричны относительно горизонтальной оси. Поскольку значение _ выбиралось произвольным, можно сделать вывод о том, что участки АФХ, соответствующие  > 0 и  < 0, симметричны относительно горизонтальной оси. Участок соответствующий  < 0, принято показывать пунктирной линией (рис. 22).

Итак, АФХ может быть построена двумя способами: с использованием ВЧХ и МЧХ (декартовых координат) или с использованием АЧХ и ФЧХ (полярных координат). При правильном построении оба способа должны давать одинаковый результат.

Точное построение АФХ требует численного расчета и может быть выполнено с помощью компьютера. Однако для решения практических задач, как правило, можно ограничится приближенным построением АФХ вручную с точным расчетом отдельных точек.

Требования к приближенному построению АФХ:

1. Построение подробно выполняется для . Для отрицательных частот вторая половина АФХ строится с учетом ее симметрии относительно горизонтальной оси.

2. Должны быть определенны квадранты, в которых проходит АФХ.

3. Должны быть найдены и указаны точки АФХ, соответствующие частотам  = 0 и . При отсутствии таких точек (асимптотический характер кривой) должны быть найдены соответствующие асимптоты и правильно показан вид участков, соответствующих и .

4. Должны быть найдены и указаны частоты, соответствующие точкам пересечения АФХ с осями координат, и координаты таких точек.

5. Направление увеличения частоты указывается на АФХ стрелкой.

Пример 9.

Апериодическое звено 1-го порядка.

На рис. 6 и 7 показаны АЧХ и ФЧХ данного звена. По этим графикам может быть установлено следующее:

- при  > 0 значения ФЧХ лежат в пределах от 0 до , следовательно, АФХ при  > 0 лежит в 4 квадранте, точек пересечения АФХ с осями координат при 0 <  <  нет;

- при =0 А()=k, ()=0, следовательно, вектор, направленный в точку АФХ при  = 0 имеет длину k и совпадает с положительной вещественной полуосью;

- при А()= 0, , следовательно, при АФХ приходит в начало координат вдоль вертикальной оси. АФХ показана на рис. 23 (точный расчет позволяет установить, что АФХ в данном примере представляет собой окружность).

П

роверим результат по второй паре частотных характеристик. ВЧХ и МЧХ данного звена показаны на рис. 18 и 19. По этим графикам может быть установлено следующее:

- при  > 0 горизонтальные координаты всех точек АФХ положительны (U() > 0), вертикальные координаты – отрицательны (V() < 0)), следовательно, при >0 АФХ лежит в четвертом квадранте и не пересекает оси координат;

- при  = 0 точка АФХ имеет декартовы координаты (U(0); V(0)) = (k; 0);

- при точка АФХ имеет координаты (0; 0).

Представленная на рис. 23 АФХ полностью соответствует указанным результатам.

Пример 10. Идеальное дифференцирующее звено.

W(s) = ks; W(j) = kj; A() = k;

; U() = 0; V() = k

Г

рафики частотных характеристик показаны на рис. 24.

По АЧХ и ФЧХ можно установить следующее:

-

при  > 0 , следовательно, на всех положительных частотах векторы, направленные в точки АФХ (и сами точки АФХ) лежат на положительной вертикальной полуоси;

- при  = 0 A() = 0, при , при увеличении частоты точки АФХ удаляются от начала координат.

Аналогичные выводы можно сделать, анализируя ВЧХ и МЧХ.

АФХ представлена на рис. 25. Характеристика совпадает с вертикальной осью.

Следующий пример требует особого внимания. Он показывает, что в ряде случаев только одна пара характеристик (АЧХ и ФЧХ или ВЧХ и МЧХ) не дает всей необходимой информации для приближенного построения АФХ.

Пример 11. Интегрирующее звено с замедлением.

; .

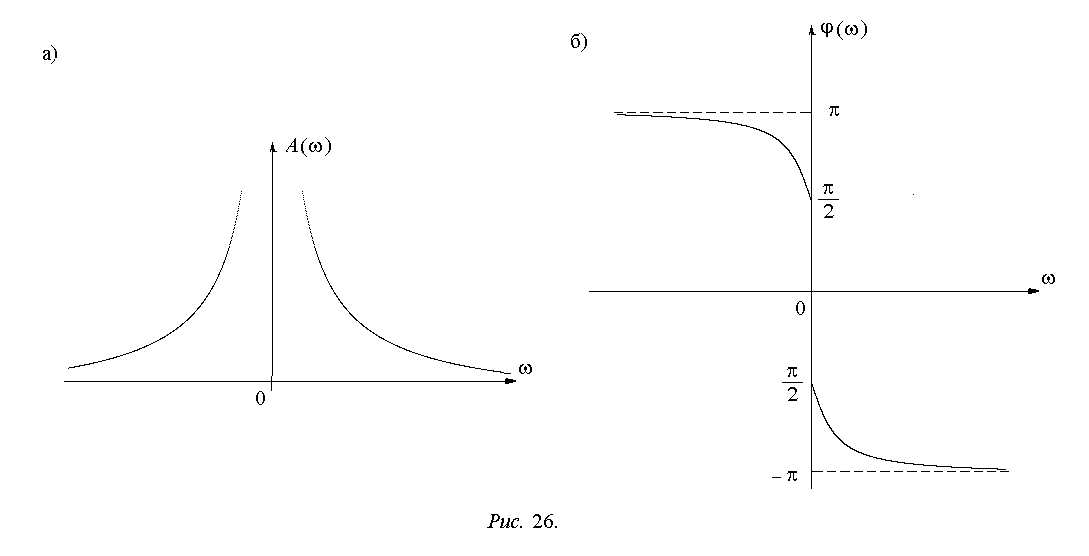
Выражения для АЧХ и ФЧХ имеют вид:

, .

Их графики показаны на рис. 26.

П

о АЧХ и ФЧХ можно установить следующее:

-

при  > 0 значения ФЧХ лежат в пределах от до , следовательно, АФХ при  > 0 лежит в третьем квадранте, точек пересечения АФХ с осями координат нет;

- при длина вектора, направленного в точки АФХ, стремится к бесконечности, угол наклона - к значению , следовательно, АФХ уходит вниз в бесконечность (при этом степень ее удаления от вертикальной оси установить не удается);

- при A() = 0, () = , следовательно АФХ стремится в начало координат вдоль горизонтальной оси;

- длина вектора направленного в точки АФХ, и угол его наклона изменяются монотонно.

Варианты АФХ, соответствующие полученным результатам (с учетом неопределенности при ), показаны на рис. 27.

Дополнительную информацию, позволяющую уточнить поведение АФХ на малых частотах, можно получить по ВЧХ и МЧХ. Получим выражения для этих характеристик и построим примерные графики (рис. 28):

,

, .

По графику и из соответствующего выражения нетрудно установить, что горизонтальная координата точек АФХ при стремится к значению –kT. Это позволяет сделать вывод о том, что правильная АФХ для данного примера – кривая 2 на рис. 27. Причем асимптотой АФХ при и является вертикальная прямая, пересекающая горизонтальную ось в точке с координатой –kT.

Отметим, что попытка выполнить приближенное построение АФХ по ВЧХ и МЧХ также вызовет затруднения: по графикам, показанным на рис. 28, не удается установить асимптотический характер АФХ при (характеристика приходит в начало координат вдоль горизонтальной оси).

Таким образом, при построении АФХ целесообразно использовать обе пары частотных характеристик: АЧХ и ФЧХ, ВЧХ и МЧХ – для получения полной информации или, по крайней мере, для проверки результата.

Пример 12. Апериодическое звено 2 порядка.

; .

Выражения для АЧХ и ФЧХ имеют вид:

, .

Их графики показаны на рис. 29.

П

о графикам на рис. 29 можно установить следующее:

- при  > 0 значения ФЧХ отрицательны и монотонно изменяются от 0 до , следовательно, АФХ при  > 0 начинается в четвертом и заканчивается в третьем квадранте, смене квадрантов соответствует точка пересечения АФХ с осью координат (вертикальной) на некоторой ненулевой частоте;

- при  = 0 A() = k, соответствующая точка АФХ лежит на положительной горизонтальной полуоси;

- при увеличении частоты длина вектора, направленного в точку АФХ, монотонно уменьшается (кривая АФХ приближается к началу координат);

- при , АФХ заканчивается в начале координат;

- вторая половина АФХ, соответствующая отрицательным частотам, может быть получена отражением относительно горизонтальной оси.

В

ид АФХ показан на рис. 30. Поскольку имеются точки пересечения АФХ с осями координат, требуется их расчет. В точке пересечения положительной ветви АФХ с вертикальной осью имеет место . Отсюда может быть получено уравнение для определения соответствующей частоты _:

.

Очевидно, при решать такое уравнение затруднительно. В то же время, можно отметить, что рассматриваемой точке соответствует и другое условие: U(₁) = 0Поэтому уравнение для определения _ может быть получено и другим способом – на основе выражения для ВЧХ. Получим выражения для ВЧХ и МЧХ:

;

, .

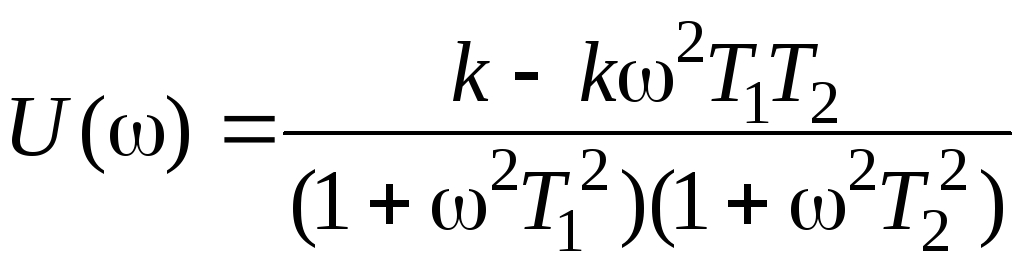Построить графики ВЧХ и МЧХ и сопоставить их с АФХ предлагается самостоятельно.

Уравнение для определения частоты _ примет вид: , откуда . Координату точки пересечения АФХ с вертикальной осью можно найти, подставив значение _ в выражение для ВЧХ:

,

или в выражение для АЧХ (в этом случае получим расстояние до искомой точки от начала координат):

.

Для отрицательных частот точка пересечения АФХ с вертикальной осью будет соответствовать частоте -_ и иметь вертикальную координату .