Пример. Определим общее число столкновений молекул h2 и Cl2 в 1 см3 смеси равных объемов газов при нормальных условиях.

Число частиц H₂ и Cl₂ в 1 см³ 1/см³.

Относительная скорость частиц см/с.

Сечение упругого соударения молекул  =1,110^-14 см².

Число соударений частиц H₂ и Cl₂ в 1 см³ за 1 секунду равно: .

Поскольку к образованию новых молекул приводят только активные соударения, общее число соударений необходимо умножить на функцию f(E_aк), определяющую долю соударений частиц, обладающих энергией большей, чем энергия активации Е_ак:

z_a = zf(E_aк).

Функцию f(E_aк) можно получить из закона распределения Максвелла - Больцмана. Доля молекул с энергией Е большей, чем энергия активации E_ак (E>E_ак), равна:

,

где n₀ – общее число молекул в системе; n_E>Eак – число молекул, обладающих кинетической энергией большей, чем энергия активации.

Энергия активации реальных реакций, протекающих не слишком быстро и не слишком медленно, составляет величину порядка Е_ак  50 –100 кДжмоль. С учетом этого при температурах близких к стандартным доля молекул, имеющих энергию больше, чем энергия активации, составляет величину порядка ~10^-9–10^-18, т. е. доля столкновений частиц, приводящих к их взаимодействию, достаточно мала.

Таким образом, число активных соударений в зависимости от температуры равно:

.

Для многих реакций важна геометрия столкновений. Сталкивающиеся активные молекулы должны быть соответствующим образом ориентированы относительно друг друга, чтобы обеспечить возможность осуществления элементарного акта взаимодействия. Геометрия столкновения учитывается множителем р, получившим название стерического фактора. Тогда число активных соударений с учетом стерического фактора (z_а^*) будет равно: z_а^*=p z_а.

Поскольку каждое активное соударение приводит к образованию новой молекулы, то число активных соударений в единице объема в единицу времени (z_а^*) соответствует, по определению скорости химической реакции, числу элементарных актов взаимодействия в единицу времени в единице объема. Таким образом, z_а^*= v,

.

Согласно закону действующих масс, скорость химической реакции A + B  AB равна:. Следовательно, константа скорости реакцииk будет определяться выражением

или ,

где – предэкспоненциальный множитель.

Произведение сечения упругих столкновений () на среднюю скорость движения молекул () представляет собойчастотный фактор (z₀):

.

Величина z₀ пропорциональна числу столкновений молекул в единице объема в единицу времени (числу соударений при единичных концентрациях частиц). Частотный фактор слабо зависит от температуры и может считаться величиной постоянной, которая может быть вычислена из молекулярно-кинетической теории газов.

Стерический фактор р учитывает ориентацию частиц в пространстве в момент столкновения по отношению друг к другу. При благоприятной ориентации для образования новых молекул р1, при неблагоприятной ориентации р1. Таким образом, k₀=pz₀.

Теория активных соударений не позволяет рассчитать величину энергии активации. Дальнейшее развитие теории элементарных реакций связано с привлечением квантово-механического описания перестройки системы химических связей в молекулах реагирующих веществ.

Теория переходного состояния. В элементарном акте химической реакции участвуют частицы исходных веществ, которые в ходе реакции превращаются в частицы продуктов. Этот переход осуществляется, как было отмечено ранее, через образование промежуточной нестабильной частицы, включающей в себя все атомы взаимодействующих частиц, объединенные общей системой химических связей. В процессе этого превращения изменяются расстояния между ядрами атомов, входящих в частицы. В модели адиабатического приближения каждому взаимному расположению ядер атомов соответствует одно определенное значение энергии, т. е. энергия системы будет определяться взаимным расположением атомов. Зависимость потенциальной энергии системы взаимодействующих частиц от их координат можно рассматривать как поверхность в многомерном пространстве – поверхность потенциальной энергии. Наиболее наглядно эту поверхность можно проиллюстрировать на примере бимолекулярной реакции АВ + С  А + ВС, в элементарном акте которой принимают участие три атома.

В общем случае энергия трех взаимодействующих атомов зависит от расстояния между ними (r_AB и r_BC) и угла . В элементарном акте угол  полагают постоянным (угол подлета частицы С к частице АВ), например, при столкновении частиц АВ и С по направлению линии связи =180 (рис.2.1). В этом случае поверхность потенциальной энергии будет функцией двух переменных E(r_AB, r_BC). Построенная в декартовой системе координат поверхность потенциальной энергии показана на рис.2.2, а.

Рис. 2.6. Пространственное расположение трех атомов при протекании элементарного акта бимолекулярной реакции АВ + С  А + ВС

В исходном состоянии энергия системы минимальна по отношению к расположению атомов в молекуле АВ (определяется r_AB) и слабо зависит от другой координаты (r_BC). На диаграмме рис.2.2, а этому состоянию соответствует долина исходных веществ. В конечном состоянии энергия системы минимальна по отношению к расположению атомов в молекуле ВС (r_BC) и слабо зависит от другой координаты (r_AB). На диаграмме этому состоянию соответствует долина продуктов. Элементарный акт химической реакции представляет собой переход системы из долины исходных веществ с долину продуктов. Энергетически выгодно, чтобы этот переход осуществлялся через точки минимумов на поверхности потенциальной энергии.

Этот переход (путь реакции) показан стрелкой на диаграмме потенциальной поверхности, изображенной на плоскости в виде системы линий, соединяющих точки с одинаковыми значениями потенциальной энергии (рис. 2.2, б). При движении из одной долины в другую энергия системы сначала возрастает, а затем уменьшается, система преодолевает перевал (точка С). Слева располагается «высокое» плато, которое соответствует состоянию системы из трех отдельных атомов А, В, С (одновременно r_AB и r_BC  ∞). Справа поверхность «круто» поднимается вверх, поскольку одновременное уменьшение расстояний между атомами (r_AB и r_BC  0) приводит к резкому возрастанию энергии отталкивания атомов (рис. 2.2, а).

Состояние системы с максимальной энергией (точка С) называется переходным состоянием, которое соответствует образованию тремя атомами короткоживущего промежуточного соединения (активированного комплекса), обладающего повышенным запасом энергии. Таким образом, элементарная химическая реакция проходит через стадию образования активированного комплекса. Он представляет собой нестабильную молекулу, в состав которой входят все атомы исходных веществ и в которой старые химические связи еще полностью не разрушены, а новые еще полностью не образованы.

Рис.2.7. Поверхность потенциальной энергии реакцииАВ + С  А + ВС (а)

и изолинии потенциальной энергии (б)

В рассматриваемой реакции система проходит через активированный комплекс (ABC)^:

Все параметры, относящиеся к переходному состоянию (активированному комплексу), обозначаются верхним индексом .

Если ввести понятие координаты реакции (X) – положение системы на пути перехода из начального состояния в конечное (рис.2.2, б), то изменение энергии системы в ходе элементарного акта будет представлять собой функцию одной переменной E(X). Вид этой зависимости представлен на энергетической диаграмме рис.2.3.

Рис. 2.8. Диаграмма изменения энергии системы в ходе реакции АВ+С  А+ВС

Максимум на диаграмме (точка С) соответствует переходному состоянию. Энергия активации реакции соответствует энергии образования активированного комплекса. Это энергия, которой должны обладать частицы, для того чтобы произошел элементарный акт химической реакции.

Необходимо отметить, что теория переходного состояния базируется на ряде допущений (постулатов). Элементарные акты проходят по пути преодоления самого низкого энергетического барьера, т. е. через образование активированного комплекса. Расчет энергии активации сводится к расчету поверхности потенциальной энергии методами квантовой механики. Считается, что активированный комплекс (ABC)^ представляет собой обычную молекулу, у которой одна колебательная степень свободы заменяется на поступательное движение вдоль координаты реакции (X). Система находится все время в состоянии термодинамического равновесия. Вероятность перехода активированного комплекса в продукты реакции определяется трансмиссионным коэффициентом , который чаще всего равен единице:

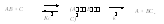
Скорость химической реакции АВ + С  А + ВС будет пропорциональна равновесной концентрации активированного комплекса: . Концентрацию активированного комплекса можно определить через константу равновесияK_C^ (см. разд. 3) реакции его образования из исходных молекул (реакция протекает при постоянном объеме и температуре Т):

, ,

следовательно, .

В теории переходного состояния константа скорости реакции распада активированного комплекса на продукты реакции определяется выражением , где – трансмиссионный коэффициент; k – константа Больцмана; h – постоянная Планка. Следовательно, скорость реакции АВ + С  А + ВС будет описываться выражением

,

в котором произведение– константа скорости реакции.

Константу равновесия можно определить через изменение термодинамических функций реакции образования активированного комплекса. Поскольку (в данном примере= –1), а

,

где А^ – изменение энергии Гельмгольца; U^ – изменение внутренней энергии, которое и является фактически энергией активации; S^ – изменение энтропии при образовании активированного комплекса, то

.

Сравнение уравнения Аррениуса и формулы для расчета константы скорости по теории переходного состояния:

дает возможность оценить значение предэкспоненциального множителя и стерический фактор р.