Конспект ТАУ / Лекция 1

Лекция 1. Основные понятия теории управления и радиоавтоматики. Фундаментальные принципы управления. Классификация систем управления. Общая характеристика задач анализа и синтеза систем

Основное содержание теории управления составляют математические методы анализа и синтеза систем. Основные задачи анализа - исследование свойств системы, прежде всего, устойчивости (в большинстве случаев неустойчивая система неработоспособна) и оценка показателей ее качества. Основные задачи синтеза – корректировка существующей системы или построение новой системы в соответствии с требованиями к ее свойствам и качеству.

Управление - это организованное воздействие на объект с целью обеспечения требуемого течения процесса в объекте или требуемого изменения его состояния.

Рисунок 1 графически интерпретирует это понятие.

На рисунке 1:

ОУ – объект управления;

y – выходной сигнал, характеризующий текущее состояние объекта управления;

g – задающее воздействие, описывающее требуемое состояние объекта управления (цель управления);

u – сигнал управления;

УУ – устройство управления (регулятор);

f – возмущающее воздействие – нерегулируемое воздействие внешней среды.

Классификация систем управления определяет выбор используемого математического аппарата и проводится по нескольким признакам. Мы ограничимся основными из них.

1. По принципу управления различают:

1а. Разомкнутые системы, общая структура которых соответствует рисунку 1. Конкретный пример представлен на рисунке 2. Здесь управляющий сигнал формируется в зависимости только от задающего воздействия. При появлении возмущающего воздействия разомкнутая система управления на него никак не реагирует, что приводит к непредсказуемому отклонению состояния объекта от требуемого. Поэтому разомкнутая система управления сама по себе неработоспособна.

1б. Замкнутые системы, реализующие управление на основе принципа обратной связи – формирование сигнала управления на основе сравнения текущего состояния объекта управления с требуемым (рисунок 3).

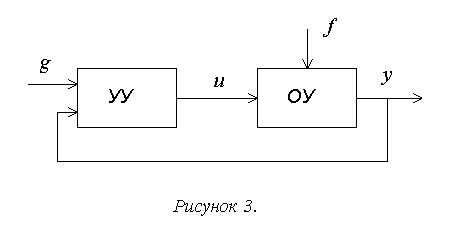
Простейший и основной вариант реализации принципа обратной связи – жесткая единичная отрицательная обратная связь. В этом случае сигнал управления формируется в соответствии с уравнением:

u(t)=k(g(t) – y(t)). (1.1)

Примеры замкнутых систем представлены на рисунках 4, 5.

Более подробная классификация замкнутых систем проводится по виду обратной связи.

1в. Системы с компенсацией возмущения. Принцип компенсации возмущающего воздействия предусматривает измерение или оценку (идентификацию) величины возмущающего воздействия и использование этой информации для формирования управляющего сигнала (рисунки 6, 7)

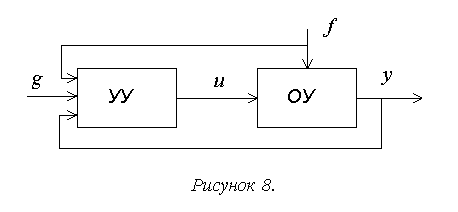
1г. Системы комбинированного управления реализуют сочетание рассмотренных выше принципов. Наиболее распространенный вариант – замкнутая система с компенсацией возмущения (рисунки 8,9).

1д. Адаптивные системы. Принцип адаптивного управления состоит в накоплении в процессе работы системы информации о поведении объекта управления и характеристиках внешней среды и использовании этой информации для корректировки структуры и параметров закона управления (настройки устройства управления).

2. По цели управления различают:

2а. Системы стабилизации: g=const. К их числу относятся все рассмотренные примеры.

2б. Системы программного управления: g= g(t). Пример – система управления ракетой-носителем. При выведении спутника на заданную орбиту законы изменения высоты, скорости, направления движения и пр. рассчитываются заранее. Задачей системы управления является обеспечение их изменения по заданным законам.

2в. Следящие системы: g=var. Пример – система управления антенной радиолокационной станции наблюдения за воздушной обстановкой. Задачей системы является обеспечение совмещения оси антенны с летательным аппаратом при заранее неизвестном законе его движения.

2г. Системы терминального управления. Пример – система самонаведения ракеты. Задачей системы является обеспечение минимального расстояния от ракеты до цели (промаха) в определенный конечный момент времени.

2д. Системы экстремального управления. Такие системы строят, когда в процессе управления требуется обеспечить максимум или минимум некоторых показателей (критериев оптимальности). Пример – система мягкой посадки космического летательного аппарата. Задачей системы является обеспечение мягкой посадки при заранее неизвестных начальных скорости и высоте с минимальным расходом топлива.

3. По структуре различают одномерные (со скалярными входными сигналами) и многомерные (с векторными входными сигналами) системы управления.

4. По форме математического описания различают линейные и нелинейные системы.

4а. Линейной является системы, для всех элементов которой может быть получено математическое описание в форме линейных алгебраических или дифференциальных уравнений.

4б. Если хотя бы один элемент системы не может быть описан линейным уравнением, вся система рассматривается как нелинейная.

5. По характеру изменения параметров различают.

5а. Стационарные системы, у которых все параметры постоянны во времени.

5б. Если в системе содержится звено, хотя бы один параметр которого зависит от времени, она рассматривается как нестационарная. Например, для системы управления летательным аппаратом, как правило, приходится учитывать изменение массы объекта управления по мере расходования топлива.

6. По характеру процесса в системе различают:

6а. Непрерывные и дискретные системы. Теория дискретных систем начала развиваться вместе с появлением первых компьютерных (цифровых) управляющих устройств. В цифровом устройстве выполняется дискретизация сигналов как по времени, так и по уровню.

6б. Системы детерминированные, стохастические и нечеткие.

Стохастической является система, хотя бы один параметр которой является случайной величиной или хотя бы один входной сигнал – случайным процессом. Случайность предполагает наличие некоторых статистических закономерностей, описываемых законом распределения, моментами распределения, корреляционной функцией и пр.

Если закономерности, которым подчиняются значения какого-либо параметра системы или входного сигнала, отсутствуют или учет их нецелесообразен, имеет место неопределенность, и рассматриваемая система классифицируется как нечеткая.

6в. Системы с запаздыванием содержат хотя бы одно звено, характеризующееся свойством запаздывания. Суть данного свойства состоит в том, что реакция звена на изменения входного сигнала начинает проявляться через некоторый постоянный момент времени.

Свойством запаздывания обладают любые цифровые устройства, а также реле.

Переходя к характеристике задач анализа и синтеза систем, рассмотрим развитие процесса в замкнутой системе стабилизации с единичной отрицательной обратной связью. На рисунке 10 показан пример процессов изменения выходного сигнала y(t) и сигнала ошибки x(t)=g(t)-y(t) в такой системе.

Если начальное значение выходного сигнала нулевое, то в момент времени подачи входного сигнала g=g₀ сигнал ошибки скачкообразно изменяется от 0 до g₀.

Точка «1» соответствует неизбежному с учетом инерционности реальных устройств продолжению роста выходного сигнала после достижения требуемого уровня g₀.

Отметим два обстоятельства, иллюстрирующие принцип действия обратной связи:

- по мере возрастания выходного сигнала (приближения текущего состояния объекта управления к требуемому) в соответствии с (1.1) величина сигнала управления, а вместе с ней и скорость роста выходного сигнала снижаются;

- после перехода выходного сигнала через требуемый уровень сигнал ошибки, а вслед за ним и сигнал управления, меняют знак, и начинается процесс торможения.

В точке «2» скорость изменения выходного сигнала меняет знак, и он начинает уменьшаться до требуемого уровня. Дальнейшее развитие процесса подчиняется отмеченным закономерностям.

Использование управления на основе принципа обратной связи не гарантирует развитие процесса управления в соответствии с рисунком 10. При увеличении коэффициента усиления k в уравнении (1.1) закона управления возможно получение законов изменения выходного сигнала, показанных на рисунках 11, 12.

В последнем случае система оказывается неработоспособной, так как цель управления не достигается. Работоспособной за исключением особых случаев может быть только устойчивая система управления. Свойство устойчивости в самом простом виде можно определить как способность системы достигать состояния равновесия.

Проверка устойчивости системы является одной из основных задач анализа.

Если в системе наблюдается процесс, соответствующий рисунку 11, устойчивость имеет место, но большие амплитуды и количество колебаний для большинства реальных систем неприемлемы (представим себе, что на рисунке 11 отображен процесс подъема лифта на 10 этаж или набора пассажирским авиалайнером требуемой высоты). Поэтому кроме качественной проверки устойчивости рассматривается также количественная оценка запаса устойчивости как степени удаления системы от границы устойчивости (рисунок 13).

Теперь отметим, что процесс, показанный на рисунках 10 и 11, в реальных системах возможен далеко не всегда. Так в системе управления двигателем (рис. 4) достижение установившегося значения выходного сигнала (скорости вращения двигателя), совпадающего по величине с g₀ невозможно, так как при y=g в соответствии с (1.1) сигнал управления (напряжение на якоре двигателя) обращается в ноль, и двигатель должен остановиться. Таким образом, в данной системе неизбежно получение установившейся ошибки (рисунок 14), значение которой является количественной характеристикой точности системы.

Добавим сюда характеристики быстродействия, позволяющие оценивать скорость достижения требуемого состояния системы или его малой окрестности, и отметим вторую основную задачу анализа систем – оценку показателей качества.

Основные задачи синтеза – обеспечение устойчивости и требуемых значений показателей качества системы.