Конспект ТАУ / Лекция 13

Лекция 13. Частотный критерий устойчивости Найквиста

Критерий устойчивости Найквиста предусматривает анализ устойчивости замкнутой системы по частотным характеристикам разомкнутой системы: и или АФХ разомкнутой системы, или и . Критерий Найквиста наиболее широко используется на практике по следующим причинам:

- передаточная функция и частотные характеристики для разомкнутой системы могут быть получены проще, чем для замкнутой;

- помимо анализа устойчивости обеспечивается определение ряда показателей качества системы;

- для анализа устойчивости и качества системы в принципе не требуется математическая модель, так как критерий допускает работу с экспериментально полученными частотными характеристиками;

- критерий Найквиста положен в основу достаточно простых и удобных процедур синтеза систем;

- “классический” вариант критерия разработан для случая единичной отрицательной обратной связи, но легко распространяется и на общий случай.

Критерий Найквиста проще всего может быть получен как следствие критерия Михайлова.

Отметим следующие обстоятельства:

1. Для системы с единичной отрицательной обратной связью имеет место следующее соотношение:

.

Следовательно, при любом изменении частоты полное приращение аргумента _1+W комплексной функции равно разности полных приращений аргумента _D характеристического комплекса замкнутой системы и _Q характеристического комплекса разомкнутой системы : _1+W =_D -_Q.

2. Для устойчивой замкнутой системы при изменении частоты от - до полное приращение аргумента составит _D =n.

3. Полное приращение аргумента при изменении частоты от - до составит _Q =n-2l, где l - количество корней знаменателя передаточной функции разомкнутой системы, лежащих в правой полуплоскости.

В результате получим необходимое и достаточное условие устойчивости замкнутой системы в следующей форме: полное приращение аргумента при изменении частоты от - до должно составлять

,

где l - количество корней знаменателя передаточной функции разомкнутой системы, лежащих в правой полуплоскости.

Если обратиться к комплексной плоскости, это условие можно сформулировать следующим образом: при изменении частоты от - до угол поворота изображающего вектора функции относительно начала координат должен составить 2l, где l - количество корней знаменателя передаточной функции разомкнутой системы, лежащих в правой полуплоскости.

Эквивалентное и значительно более удобное для практического использования условие можно получить, рассматривая непосредственно ЧПФ разомкнутой системы W(j и соответственно сместив опорную точку для измерения угла поворота из начала координат в точку (-1; 0j).

Таким образом получаем основную формулировку критерия устойчивости Найквиста: для устойчивости замкнутой системы необходимо и достаточно, чтобы при изменении частоты от - до угол поворота изображающего вектора ЧПФ разомкнутой системы относительно точки с координатами (-1; 0j) составил 2l, где l - количество корней знаменателя передаточной функции разомкнутой системы, лежащих в правой полуплоскости.

Иногда говорят: АФХ разомкнутой системы должна охватить точку с координатами (-1; 0j) l раз в положительном направлении.

Рассмотрим применение критерия для основных частных случаев.

Система, устойчивая в разомкнутом состоянии

В этом случае l=0, для устойчивости замкнутой системы угол поворота изображающего вектора относительно точки с координатами (-1; 0j) должен быть равен нулю, то есть АФХ разомкнутой системы не должна охватывать эту точку.

Пример: передаточная функция разомкнутой системы

.

Получим АЧХ и ФЧХ:

, .

АФХ разомкнутой системы показана на рисунке 98. С учетом сформулированного выше условия рисунок 98а соответствует устойчивой замкнутой системе, рисунок 98б – неустойчивой, рисунок 98в – находящейся на колебательной границе устойчивости. В последнем случае частота _, соответствующая прохождению АФХ через точку (-1; 0j), является частотой незатухающих колебаний в системе.

Из рисунка 98 следует порядок применения критерия: по виду АФХ с учетом значения l определяется требуемое для устойчивости замкнутой системы взаимное расположение точки пересечения АФХ с горизонтальной осью и точки (-1; 0j). После этого весь расчет связан с точкой пересечения. Найдем для рассматриваемого примера частоту _, приравняв к нулю мнимую частотную характеристику разомкнутой системы:

,

,

,

: .

В соответствии с рисунком 98а условие устойчивости замкнутой системы сводится к неравенству или .

Воспользуемся первым из них:

,

и так далее до итогового неравенства

В заключение отметим, что для применения критерия можно ограничиться половиной АФХ – для положительных частот, дополнив ее отрезком положительной вещественной полуоси.

Система, неустойчивая в разомкнутом состоянии

В этом случае l>0, и АФХ разомкнутой системы должна охватить точку с координатами (-1; 0j) l раз в положительном направлении. Целесообразно использовать полную АФХ.

Пример: передаточная функция разомкнутой системы

, T₁<T₂.

Получим АЧХ и ФЧХ:

, .

АФХ разомкнутой системы показана на рисунке 99. С учетом сформулированного выше условия рисунок 99а соответствует устойчивой замкнутой системе, рисунок 99б – неустойчивой. Условие устойчивости замкнутой системы сводится к неравенству или . В результате получаем k>1. Система может быть только условно устойчивой.

Система, нейтрально устойчивая в разомкнутом состоянии

Полученная выше формулировка критерия Найквиста распространяется на системы, устойчивые (l=0) и неустойчивые (l >0) в разомкнутом состоянии. Для того, чтобы критерий был универсальным, необходимо также учесть системы, находящиеся в разомкнутом состоянии на границе устойчивости, то есть учесть случаи, когда знаменатель передаточной функции разомкнутой системы Q(s) имеет нулевые

или мнимые корни. Это удается сделать, условно относя системы, находящиеся на границе устойчивости, к числу устойчивых. В таком контексте их называют нейтрально устойчивыми. Формально этот прием сводится к тому, что нулевой корень рассматривается как предельный случай отрицательного вещественного корня: s₁=→, а пара мнимых корней – как предельный случай комплексно сопряженных с отрицательной вещественной частью: s_1,2=±j→.

Рассмотрим два следующих примера.

Для передаточной функции разомкнутой системы

АЧХ и ФЧХ описываются выражениями:

, .

АФХ системы показана на рисунке 100а.

Для передаточной функции разомкнутой системы

АЧХ и ФЧХ описываются выражениями:

, .

АФХ системы показана на рисунке 100б.

В обоих случаях применить критерий не удается, так как АФХ претерпевают разрыв на частоте, соответствующей нулевым корням полиномов Q, то есть при =0.

Рассмотрим первую из этих систем как предельный случай рассмотренной выше системы (рисунок 98), представив передаточную функцию в форме

,

где , , .

Обратимся к малому диапазону частот в окрестности нуля ’<<’, где , . Для этого диапазона получим:

,

,

.

С учетом величины k’ и T₃ отметим, что при изменении частоты от ’ до ’ значение ФЧХ изменится от до при сохранении бесконечно больших значений ФЧХ. Следовательно, для АФХ на рисунке 98 участок, лежащий в первом и четвертом квадрантах, деформируется в дугу бесконечно большого радиуса длиной , движение по которой при увеличении частоты происходит по часовой стрелке.

Если теперь вернуться к исходному виду АФХ (рисунок 100а) и полному диапазону частот от - до , можно дополнить ее дугой бесконечно большого радиуса длиной  в направлении по часовой стрелке. Благодаря этому АФХ становится замкнутой кривой, что позволяет однозначно применить критерий устойчивости Найквиста (рисунок 101).

В соответствии с рисунком 101 с учетом l=0 для устойчивости замкнутой системы должно иметь место или . Найдем _:

,

,

,

: .

Получим условие устойчивости:

,

.

Аналогичные рассуждения для общего случая с кратными нулевыми корнями знаменателя передаточной функции разомкнутой системы

дают увеличение длины дополняющей дуги в r раз, где r – кратность корня.

Для рассмотренного выше примера с r=3 АФХ, представленную на рисунке 100б, потребуется дополнить дугой длиной 3, в результате чего ее анализ становится весьма трудоемким.

В таких случаях допустимо применение приема, использованного выше для систем, устойчивых в разомкнутом состоянии, – ограничиться половиной АФХ – для положительных частот, дополнив положительной вещественной полуосью и дугой бесконечно большого радиуса длиной .

Построение для рассматриваемого примера выполнено на рисунке 102.

Из рисунка видно, что условие устойчивости данной системы может быть получено на основе неравенства или . Воспользуемся первым из них.

Найдем частоту _:

,

,

,

, .

Получим условие устойчивости:

,

,

.

Теперь рассмотрим пример системы, находящейся в разомкнутом состоянии на колебательной границе устойчивости:

.

АЧХ и ФЧХ описываются выражениями:

, .

АФХ системы для показана на рисунке 103.

Прямо применить критерий, как и выше, не удается, так как АФХ претерпевают разрыв на частоте , соответствующей мнимым корням полинома Q. В окрестности этой частоты , ФЧХ изменяется скачкообразно на величину .

Воспользуемся тем же, что и ранее, приемом и представим рассматриваемую передаточную функцию в следующей форме

где .

Теперь выражения для АЧХ и ФЧХ примут вид:

,

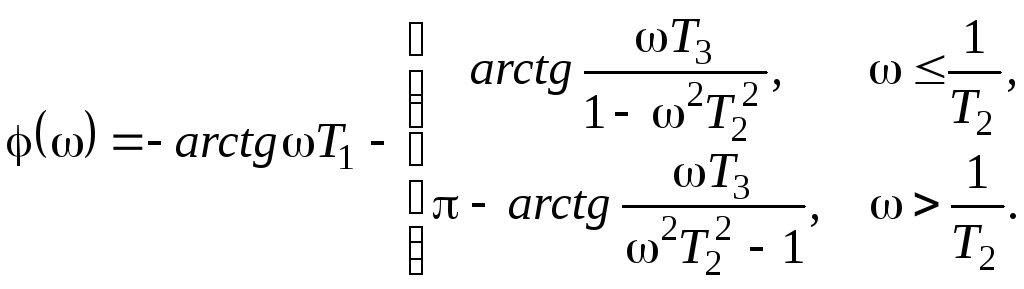
С учетом величины T₃ и известных свойств колебательного звена отметим, что величина резонансного пика в окрестности частоты будет стремиться к бесконечности и в той же малой окрестности произойдет изменение значений ФЧХ на величину, стремящуюся к .

В результате приходим к тому же правилу дополнения АФХ дугой бесконечно большого радиуса длиной  в отрицательном направлении (по часовой стрелке) на частоте, соответствующей мнимому корню знаменателя передаточной функции разомкнутой системы.

Дополненная таким образом АФХ для рассматриваемого примера представлена на рисунке 104, который позволяет сделать вывод о неустойчивости этой системы независимо от значений ее параметров.

Итак, при наличии в знаменателе передаточной функции разомкнутой системы нулевых и чисто мнимых корней для использования критерия Найквиста АФХ разомкнутой системы дополняется дугами бесконечно большого радиуса в направлении по часовой стрелке на всех частотах, соответствующих таким корням. Длина каждой дуги r, где r – кратность корня.

При использовании для анализа устойчивости ветви АФХ, соответствующей положительным частотам, она дополняется в окрестности  положительной вещественной полуосью и дугой бесконечно большого радиуса длиной .

Отметим еще одну форму критерия Найквиста, эквивалентную рассмотренной. Она основана на подсчете переходов АФХ через отрезок вещественной оси, лежащий левее точки (-1; 0j). «Положительным» называют переход в направлении против часовой стрелки, соответствующем положительному направлению отсчета углов, «отрицательным» - переход в противоположном направлении. Если АФХ или рассматриваемая ее часть начинается на указанном участке, имеет место «полупереход» с соответствующим направлению АФХ знаком.

В таких терминах критерий сводится к соблюдению равенства:

,

если рассматривается полная АФХ, или для ветви АФХ, соответствующей положительным частотам

,

где n₍₊₎ – количество «положительных» переходов, n_(-) – количество «отрицательных» переходов, l - количество корней знаменателя передаточной функции разомкнутой системы, лежащих в правой полуплоскости.

Обобщение критерия Найквиста на системы с произвольной обратной связью

Устойчивость – это собственное свойство системы, не зависящее от наличия и точек приложения входных сигналов, а также от точки наблюдения процесса в системе. Поэтому для системы с произвольной обратной связью (рисунок 105а) можно формально перенести точку, в которой наблюдается выходной сигнал (рисунок 105б), и получить следующий вывод: при использовании критерия Найквиста для системы с произвольной обратной связью следует рассматривать годограф произведения передаточных функций прямой цепи и обратной связи .