Конспект ТАУ / Лекция 18

Лекция 18. Способы повышения точности линейных систем

Вернемся к полученным в предыдущей лекции результатам расчета установившейся ошибки от задающего воздействия.

Для статической системы: , где g₀ – величина ступенчатого задающего воздействия, k – коэффициент усиления разомкнутой системы.

Для системы с астатизмом первого порядка: , где v – скорость изменения задающего воздействия. С учетом такого влияния коэффициента усиления на величину ошибки для систем с астатизмом первого порядка коэффициент усиления иногда называют добротностью по скорости и обозначают k_v.

Для системы с астатизмом второго порядка: , где  – ускорение, с которым изменяется задающее воздействие. Поэтому для систем с астатизмом второго порядка коэффициент усиления иногда называют добротностью по ускорению и обозначают k_.

Из рассмотренных выражений следует, что величина установившейся ошибки системы по задающему воздействию может быть уменьшена путем увеличения коэффициента усиления разомкнутой системы.

Анализ аналогичных соотношений для ошибки от возмущения позволяет сделать аналогичный вывод по отношению к коэффициенту передачи участка системы до точки приложения возмущения.

Однако увеличение коэффициента усиления нельзя признать универсальным способом, так как для абсолютно устойчивых систем оно может вызвать снижение запаса устойчивости или даже потерю устойчивости системы. Поэтому одновременно с увеличением коэффициента k приходится вводить в САУ корректирующие (демпфирующие) средства. Разработаны и другие способы повышения точности.

В качестве первого примера для анализа различных способов повышения точности рассмотрим систему, структурная схема которой показана на рисунке 120.

Примем k_о=2, T=1 c.

Структурные признаки показывают, что данная система не имеет астатизма ни по задающему, ни по возмущающему воздействиям. Поэтому получим для нее расчетные соотношения для ошибок от ступенчатых входных сигналов и :

, ;

;

;

, ;

;

.

Очевидно, с точки зрения точности системы, желательно повышать ее коэффициент передачи, причем для снижения ошибки от возмущения это следует делать за счет повышения коэффициента передачи участка прямой цепи до точки приложения возмущающего воздействия.

Проанализируем устойчивость рассматриваемой системы:

,

.

В результате получаем условие устойчивости в виде k<8, то есть при исходных параметрах рассматриваемая система находится на границе устойчивости.

Предположим, что требуемый запас устойчивости составляет 14 Дб. Тогда общий коэффициент передачи разомкнутой системы должен быть снижен в 5 раз.

Введем в систему простейшее устройство управления в форме П-регулятора (пропорционального регулятора). Его передаточная функция имеет вид W_р(s)=k₁, а уравнение: u(t)=k₁x(t)=k₁[g(t)-y(t)]. Для обеспечения необходимого запаса устойчивости системы нужно задать k₁=0,2 (рисунок 121).

Теперь величина общего коэффициента передачи разомкнутой системы составит , а установившаяся ошибка от задающего воздействия , то есть почти 40% от его величины.

Оценим и ошибку от возмущения: .

Точность системы, очевидно, неудовлетворительна.

Таким образом, “прямой” способ повышения точности путем повышения коэффициента передачи системы дает весьма ограниченные возможности.

Рассмотрим ряд более эффективных способов.

Введение производной в закон управления.

Этот способ непосредственно реализуется путем введения в систему пропорционально-дифференциального (ПД) регулятора с уравнением и соответственно передаточной функцией (рисунок 122). Для удобства передаточную функцию регулятора представим в форме , .

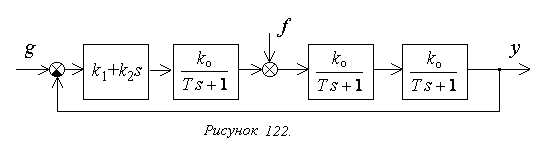
Получим характеристический полином и проанализируем устойчивость системы:

, ;

,

.

Условие устойчивости получим в виде:

.

Сравнивая это условие с полученным для исходной системы, видим, что за счет выбора величины  можно увеличить критическое значение коэффициента передачи и соответственно расширить границы изменения коэффициента k₁ регулятора.

Так для повышения критического значения от 8 до 40 нужно обеспечить и соответственно , с.

При этом для обеспечения запаса устойчивости по амплитуде величиной 14 Дб можно задать k=8, соответственно k₁=1, и получить:

,

;

,

.

Установившиеся ошибки снижаются более, чем в 3,5 раза.

При практической реализации данного способа чаще используют гибкую обратную связь (рисунок 122а).

Нетрудно убедиться, что характеристический полином замкнутой системы и результаты расчета установившихся ошибок для такой системы не изменятся по сравнению со случаем использования ПД-регулятора.

Для построения гибкой обратной связи рассмотренного вида необходимо обеспечить измерение как самой регулируемой величины, так и скорости ее изменения. Например, для рассмотренной в начале семестра следящей системы выходным сигналом является угол.

Гибкая обратная связь, обеспечивающая введение производной в закон управления, может быть построена путем добавления в систему тахогенератора.

Рассмотренный способ повышения точности можно охарактеризовать как косвенный. Само по себе введение производной в закон управления не приводит к повышению точности системы, но позволяет повысить ее запас устойчивости и увеличить коэффициент усиления, определяющий точность.

Введение интеграла в закон управления.

Дополним рассмотренную выше в качестве первого примера систему устройством управления, реализующим интегральный закон управления , то есть идеальным интегрирующим звеном (рисунок 123).

В соответствии со структурными признаками астатизма можно сделать вывод, что данный способ обеспечивает повышение порядка астатизма по всем рассматриваемым входным сигналам.

Проанализируем устойчивость системы:

, ;

,

,

.

Условие устойчивости получим в виде:

.

Критическое значение коэффициента усиления по сравнению с исходной системой снизилось в 9 раз. Для обеспечения требуемого запаса устойчивости необходимо снизить величину общего коэффициента усиления до k=0,18.

Таким образом, недостатком данного способа повышения точности является значительное снижение запаса устойчивости системы.

Рассмотрим более подробно пример следящей системы.

Система имеет первый порядок астатизма по задающему воздействию и является статической по возмущению.

Применим интегральный закон управления (рисунок 124).

Теперь, очевидно, по возмущению система получила астатизм первого порядка, а по задающему воздействию порядок астатизма повышен до второго.

Проанализируем устойчивость:

,

.

Необходимое условие устойчивости не выполняется. Рассматриваемый способ нарушил устойчивость системы.

Основной недостаток рассматриваемого способа можно в значительной степени устранить путем применения пропорционально-интегрального закона управления, или ПИ-регулятора, с законом . Передаточная функция такого регулятора соответствует изодромному звену: (рисунок 125).

Достигнутый астатизм в системе сохраняется.

Проанализируем устойчивость:

,

.

Необходимое условие устойчивости теперь выполняется, а применение критерия Гурвица позволит выбрать величину параметра в соответствии с требованиями к запасу устойчивости.

Неединичная обратная связь.

Астатизм первого порядка по задающему воздействию может быть обеспечен путем введения в систему жесткой неединичной обратной связи.

Вернемся к первому примеру и реализуем такой способ (рисунок 126).

Найдем установившуюся ошибку от задающего воздействия:

;

;

.

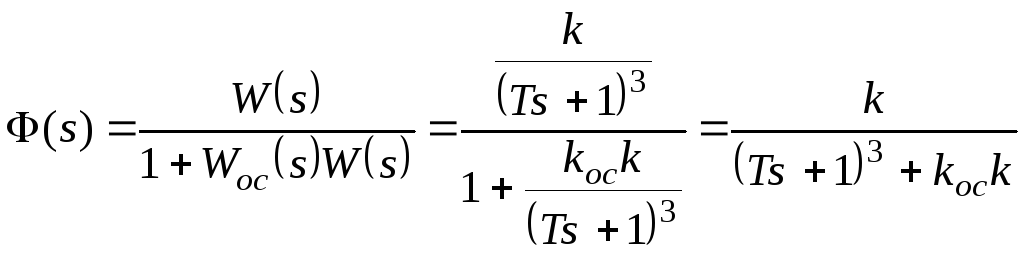Приравняв последнее выражение к нулю, получим условие обеспечения астатизма по задающему воздействию:

,

,

,

.

Предлагается самостоятельно убедиться в том, что ошибка от возмущения при этом несколько возрастет, запас устойчивости также увеличится.

Комбинированное регулирование.

Астатизм по возмущению может быть обеспечен путем дополнения структуры системы цепью компенсации возмущающего воздействия.

Структура, показанная на рисунке 127, позволяет обеспечить астатизм первого порядка по возмущающему воздействию.

Для удобства анализа преобразуем структурную схему к виду, показанному на рисунке 128 и рассмотрим раздельно преобразование системой двух возмущающих воздействий:

,

,

;

,

,

.

Суммарная ошибка от возмущающего воздействия составит:

,

откуда получим условие обеспечения астатизма по возмущению:

или .

Рассмотренный способ не влияет на ошибку от задающего воздействия, так как сигнал g(t) не проходит через цепь компенсации возмущения, и на устойчивость системы, так как указанная цепь не входит в основной замкнутый контур системы.

Недостаток данного способа связан с необходимостью точного измерения возмущающего воздействия для реализации цепи компенсации, что на практике не всегда оказывается возможным.

В заключение отметим, что рассмотренным способом теоретически можно обеспечить полную инвариантность системы к возмущающему воздействию. Для этого нужно реализовать структуру, показанную на рисунке 129.

На практике это редко оказывается возможным в силу физической нереализуемости передаточной функции (порядок ее числителя превышает порядок знаменателя).