24. Теорема Ролля. Геометрический смысл.

Теорема Ролля (Ролль, 1652-1719 – французский математик).

     Если функция f(x)непрерывна на сегменте[a, b], дифференцируема во всех его внутренних точках и на концах сегмента обращается в нуль, то естьf(a)=f(b)=0,то ее производнаяf^/(x)обращается в нуль хотя бы в одной внутренней точкеx=cэтого сегмента.

Доказательство. Так как функция непрерывна на сегменте, то она достигает на этом сегменте своего наибольшегоМи наименьшего значенияm(смотри свойства функций, непрерывных на сегменте).

     Если M=m, то функция постоянна на сегменте[a, b]и, следовательно,f^/(x)=0в любой точке этого сегмента.

     Пусть Mm, тогда одно из этих чисел, например,M0. Поэтому, если наибольшее значениеМ достигается в точкеc:f(c)=M,то точкасдолжна быть внутренней точкой сегмента[a, b],то есть должна принадлежать интервалу (a, b)(так как на концах сегментаf(a)=f(b)=0).

     Следовательно, по теореме Ферма f^/(c)=0.

Замечание. Теорема Ролля верна и в том случае, еслиf(a)=f(b)0.

Геометрический смысл.

Если график непрерывной на сегменте [a, b]и дифференцируемой внутри него функции пересекает осьOx в двух точкахx=aиx=b, то между этими точками найдется хотя бы одна точкас, a<c<b,в которой касательная к графику параллельна оси абсцисс.

Замечание. Нарушение хотя бы одного из условий теоремы Ролля может привести к тому, что для соответствующей функции заключение теоремы не будет справедливо.

Здесь нарушена непрерывность внутри отрезка[a, b].

Здесь нарушена непрерывность в точкеx=a.

25. Теорема Лагранжа о конечных приращениях. Геометрический смысл.

26. Уравнение касательной и нормали к плоской кривой.

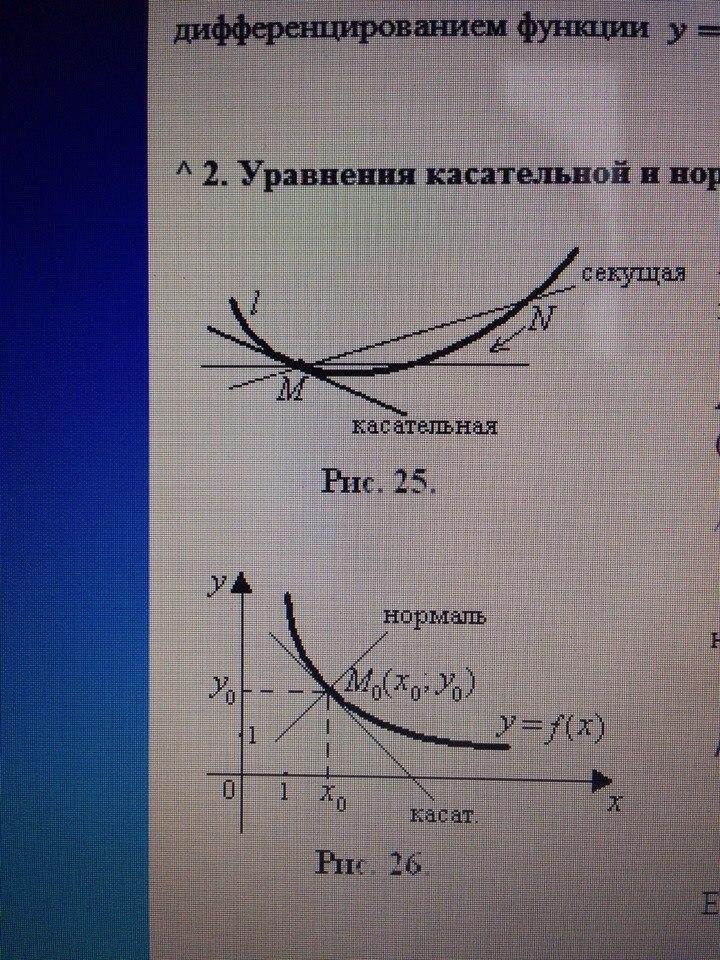
Касательной к кривой l в ее точке М называют предельное положение секущей MN, когда точка N, двигаясь по кривой l, неограниченно приближается к точке М (рис. 25).

Нормалью к кривой называется прямая, перпендикулярная касательной к этой кривой и проходящая через точку касания (рис. 26).

y = f '(x0)·(x – x0) + f(x0) (уравнение касательной)

Уравнение нормали к кривой

27. Правило Лопиталя. Раскрытие неопределенностей 0/0, ∞/ ∞, 0* ∞, 1^ ∞, 0^0, ∞ˆ0.

Неопределенность вида 0/0. Первое правило Лопиталя.

Если =0,то

когда последний существует.

 Неопределенность вида ?/?. Второе правило Лопиталя.

Если =?,то

 когда последний существует.

 Неопределенности вида 0Ч ??, ? - ?, 1? и 0⁰ сводятся к неопределенностям 0/0 и ?/? путем алгебраических преобразований

28. Формула Тейлора для многочлена. Формула Тейлора в произвольной точке. Формула Маклорена. Разложение в ряд Тейлора одной из функций e^x, sinx, cosx,

ln(1+x).

 Формула Тейлора для многочлена

 Формула Тейлора в произвольной точке

Pn(f)=f(a)+f'(a)*(x-a)+((f''(a)*(x-a)^2)/2!)+...((f^(n))(a)*(x-a))/n!)

Формула Маклорена

 Разложение в ряд Тейлора одной из функций e^x, sinx, cosx, ln(1+x).