Графовые модели программ, их взаимосвязь.

Сами программы описаны строго и следовательно сами по себе формальны. Но возникает ряд вопросов: как оптимизировать программу относительно использования кэша, регистров и пр. Особенно это важно при выявлении скрытого параллелизма.

Эти и подобные вопросы связаны с тонкой информационной структурой программ.

Информационная структура программ(ИСП)- совокупность сведений о том, как отдельные элементы связаны между собой.

В изучении ИСП сущ 2 подхода –

- денотационный- изучение на основе смены состояния памяти.

- операционный –представление программы в виде совокупности действий, связанных между собой

Операционный подход порождает ряд моделей, называемых графовыми. В этих моделях вершины – множество действий программ. Дуги – отношения между вершинами.

В рамках подхода рассматривается 2 вида действий – преобразователи и распознаватели. Преобразователи осуществляют переработку информации(им соответствуют напр. операторы присваивания), а распознаватели определяют последовательность выполнения преобразователей( напр if).

Рассмотрение вопроса продолжим на след примере

1 y=b1/a1

2 x=y

3 DO i=2,n

4. x=(bi-ci*x)/ai

5. if(x<=y) GO TO 7

6. y=x

7 END DO

После выполнения у буде равно максимальному элементу Х. 1,2,4,6 - преобразователи.

3,5,7- распознаватели.

Между действиями устанавливается 2 типа отношений. Первый определяет факт выполнения одного действия за другим (связь по управлению, операционная связь).

Второй – использования результатов одного действия в качестве операндов другого (информационная связь). Основываясь на первом типе отношений, поставим каждому действию вершину, а дуге отношение последовательности действия(от предшественника к последователю). Получим управляющий граф.

Теперь положим, что мы определили начальные данные программы и наблюдаем за ее действиями на обычном последовательном вычислителе. Каждое срабатывание оператора будем фиксировать вершиной. Получим множество, которое будет отличатся от графа управления. Соединив вершины дугами получим ориентированный граф, кот называется операционно-логической историей.(напр для случая n=3,B={0,1,1},A{1,1,1},C{undef,1,1})

1 2 3 4 5 6 7

1 2 3 4 5 6 7

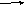
Данный граф – подмножество графа управления, однако если мы объединим всевозможные операционные графы, это не значит, что мы получим граф управления (в случае неоптимальной программы).

Опять сопоставим каждому действию вершину. Дуге же сопоставим отношение информационной связи. Получим информационный граф.

Поступим аналогично, зададим данные, получим историю реализации программы.

1 2 4 6

1 2 4 6

Все сказанное на счет операционного графа верно и для истории реализации.

Достоинства этих 4 моделей:

-существуют для всех программ(т.е. универсальны)

-возможно построение смешанных(комбинированных) моделей на их основе

-существуют преобразования, переводящие модели друг в друга.

Среди всех моделей наиболее информативна и полезна в практическом отношении четвертая. На ее основе можно ответить на любые вопросы, касающиеся реализации данного алгоритма. Напр определить множество независимых операций.

Проблема определения независимых операций сформировала целый пласт в Computer Science. Это привело к формированию идеи построения графов зависимостей. В этих моделях отношения информационной связи заменяется более широким отношением зависимости.

Два оператора зависимы, если при их выполнении происходит обращении к одной(переменной) ячейке памяти. Так как информационная связь реализуется посредством обращения к одной переменной(ячейке), то она есть частный случай зависимости. Граф зависимостей для вышеприведенного примера будет выглядеть следующим образом:

1 2 4 6

Очевидно, информационный граф является подграфом графа зависимостей. Переменные в графе зависимостей могут играть разные роли – быть как операндом, так и результатом.

Рассмотрим след пример

1 s=0

DO i=1,n

2. s=s+ai

END DO

Возможны два варианта посроения графа зависимостей

- рассматривать в качестве вершины операторы программы

1 2

-рассматривать в качестве вершины отдельное срабатывание каждого оператора,т.е. операции(n=4)

0 1 2 3 4

Заметим, что в вершину с номером n входит n дуг, c номером n-1 n-1 дуг и т д. Большое количество дуг – плата за выявление зависимостей.

Близко к графам зависимостей стоит граф влияния. Будем говорить, что одна операция влияет на другую, если изменение переменной, вычисляемой первой операцией, повлияет на другую операцию. Построим соответствующий граф(совпадает с графом зависимостей операций, но в общем случае не совпадает).

0 1 2 2 2

Будем говорить, что отношение R: АRAтранзитивно, если для любыхa,b,cпринадлежащих А

a R b,bRc=>aRc

Пример транзитивного отношения – отношение равенства “=”. Если а=bиb=c, тоa=c

Отношения управления, информационной связи и зависимости не являются транзитивными. Отношение влияния транзитивно. Граф истории реализации является остовным подграфом(минимальный граф)(граф, в кот любые две вершины соединены 1 путем, либо не соединены вовсе) графа влияния.

1 2 2 2 2

Граф влияния – транзитивное замыкание истории реализации.

Вопрос№26

MPI –общая структура