ЛЕК Устр и действ / Устройство и действие Л-1

«Устройство и действие лазерных систем»

Лекция 1:

Электромагнитное излучение и кванты

Спектральная плотность излучения абсолютно черного тела

Тепловое излучение имеет непрерывный спектр. Это означает, что нагретое тело испускает некоторое количество энергии излучения в любом диапазоне частот или длин волн. Распределение энергии излучения тела по спектру зависит от температуры тела. При этом для всех тел с увеличением температуры максимум энергии излучения смещается в коротковолновый участок спектра, а общая энергия излучения возрастает.

Так, если излучение батареи центрального отопления (350К) имеет пик энергии вдиапазоне невидимого инфракрасного излучения, то раскаленная поверхность Солнца (6000К) излучает значительную часть энергии в диапазоне видимого света, а при ядерном взрыве (1 000000К) большая доля энергии взрыва уносится коротковолновыми

рентгеновским и гамма-излучением.

Однако для этого пришлось ввести принципиально новое положение о том, что энергия,

которую несет свет, может поглощаться и испускаться не непрерывно, а отдельными порциями - квантами

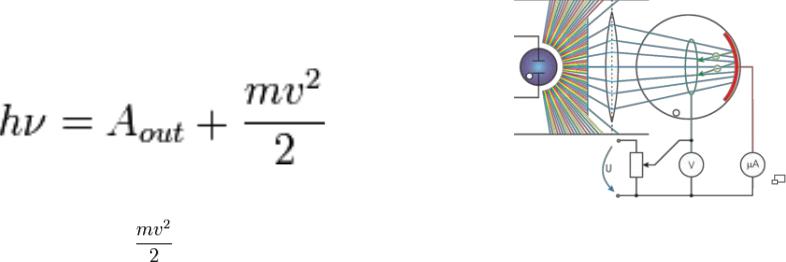
Красная граница фотоэффекта

Исследования фотоэффекта показали, что, вопреки классической электродинамике, энергия вылетающего электрона всегда строго связана с частотой падающего излучения и практически не зависит от интенсивности облучения. Фотоэффект был объяснѐн в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Карла Вильгельма Озеена, получил Нобелевскую премию) на основе гипотезы Макса Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк предположил, что свет излучается только квантованными порциями, то Эйнштейн уже считал, что свет и существует только в виде квантованных порций. Из закона сохранения энергии, при представлении света в виде частиц (фотонов), следует формула Эйнштейна для фотоэффекта:

где Aout — т. н. работа выхода (минимальная энергия, необходимая для удаления

частота падающего фотона с энергией hν, h — постоянная Планка. Из этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты, ниже которой энергии фотона уже не достаточно для того, чтобы «выбить» электрон из металла.

Схема эксперимента по исследованию фотоэффекта. Из света берется узкий диапазон частот и направляется на катод внутри вакуумного прибора. Напряжением между катодом и анодом устанавливается энергетический порог между ними. По току судят о достижении электронами анода.

Линейчатый спектр разреженных газов

Оптический линейчатый эмиссионный спектр азота

Моде́ль атома Нильса Бо́ра была предложенна в 1913 г. За основу он взял планетарную модель атома, выдвинутую Резерфордом. Однако, с точки зрения классической электродинамики, электрон в модели Резерфорда, двигаясь вокруг ядра, должен был бы излучать непрерывно, и очень быстро, потеряв энергию, упасть на ядро. Чтобы преодолеть эту проблему Бор ввел допущение, суть которого заключается в том, что электроны в атоме могут двигаться только по определенным (стационарным) орбитам, находясь на которых они не излучают, а излучение происходит только в момент перехода с одной орбиты на другую. Причем стационарными являются лишь те орбиты, при движении по которым момент количества

Энергетические уровни и квантовые переходы

Всоответствии с основными правилами квантовой механики все частицы, большие и малые, обладают дискретными уровнями энергии или состояния. Различные дискретные уровни энергии соответствуют различным периодическим движениям входящих в состав частицы электронов. В то время как самый низкий допустимый уровень энергии называют

основное состояние, все другие, относительно более

высокие энергетические уровни, называются возбужденными состояниями.

Вкачестве простой иллюстрации, рассмотрим атом водорода. Его ядро ​​имеет один протон и один электрон на орбите ядра. Этот единственный электрон может занимать только определенные

конкретные орбиты. Этим орбитам присваивается

квантовое число N, начиная с N=1. Последующим внутренним орбитам присваиваются номера N=2, N=3 … и так далее. Энергия электрона, находящегося на внутренней орбите с числом N=1, является самой низкой и, следовательно, ей соответствует состояние, называемое основным. Рисунок иллюстрирует случай

атома водорода и соответствующие возможные

уровни энергии.

Эти дискретные энергетические уровни существуют в любой форме, безотносительно от периодических движений электрона. Существуют множество типов электронных уровней, отличных от простейшей представленной схемы. Ядра различных атомов имеют свои собственные различные энергетические уровни.

Энергетические уровни и квантовые переходы

В свою очередь, молекулы, состоящие из атомов, также имеют различные энергетические уровни, зависящие от колебаний различных атомов в составе молекулы, а также энергетические уровни, соответствующие вращению самой молекулы.

Когда мы приступим к изучению различных типов лазеров, мы увидим, что все виды энергетических уровней – электронных, колебательных, вращательных – играют важные роли в излучении различных распространѐнных типов лазеров.

Переходы между электронными энергетическими уровнями, имеющими отношение к лазерному воздействию, соответствуют длинам волн, лежащим в диапазоне от ультрафиолетового до ближнего инфракрасного излучения. В качестве примеров приведѐм генерацию излучения в неодимовых лазерах (1064 нм) и аргон-ионных лазерах лазеры (488 нм): переходы между колебательными энергетическими уровнями атомов соответствуют инфракрасному диапазону. В лазерах, использующих в качестве рабочей среды углекис-

лый газ (СО2, 10 600 нм) и HF лазерах, (2700 нм), переходы между вращательными энерге-

тическими уровнями соответствуют диапазону длин волн от 100 микрон (мкм) до 10 мм.

В плотной среде, твердой, в жидкой или в газе под высоким давлением, атомы и молекулы постоянно сталкиваются, вынуждая друг друга перепрыгивать с одного уровня энергии на другой. Однако, для лазерщиков представляет интерес только случаи столкновения, вызывающие выделение энергии (фотона), то есть оптически разрешенные переходы. Оптически разрешенным переходом между двумя энергетическими уровнями называется переход, характеризующийся либо поглощением, либо испусканием фотона, который, в свою очередь удовлетворяет условиям возникновения резонанса ΔE=hν, где ΔE является разницей в энергии между двумя вовлеченными в переход уровнями энергии, h – постоянная Планка (равна 6.6260755 × 10-34 Дж/c или 4.135 669 2 × 10-15 Эв/с) и ν - частота фотона, испускаемого или поглощаемого.

Энергетические уровни и квантовые переходы

излучение кванта: ν3-2 = (Е3-Е2)/h

ν2-1 = (Е2-Е1)/h ν3-1 = (Е3-Е1)/h

поглощение кванта: ν3-1 = (Е3-Е1)/h

Квантовые переходы, скачкообразные переходы квантовой системы (атома, молекулы, атомного ядра, твѐрдого тела) из одного состояния в другое. Наиболее важными являются К. п. между стационарными состояниями, соответствующими различной энергии квантовой системы, — К. п. системы с одного уровня энергии на другой. При переходе с более высокого уровня энергии Ek на более низкий Ei система отдаѐт энергию Ek → Ei, при обратном переходе — получает еѐ (рис.). К. п. могут быть излучательными и безызлучательными. При излучательных К. п. система испускает (переход Ek → Ei) или поглощает (переход Ei → Ek ) квант электромагнитного излучения — фотон — энергии hν (ν— частота излучения, h — Планка постоянная), удовлетворяющей фундаментальному соотношению Ek - Ei = hν, (которое представляет собой закон сохранения энергии при

таком переходе). В зависимости от разности энергий состояний системы, между которыми

происходит К. п., испускаются или поглощаются фотоны радиоизлучения, инфракрасного, видимого, ультрафиолетового, рентгеновского излучения, γ-излучения. Совокупность излучательных К. п. с нижних уровней энергии на верхние образует спектр поглощения данной квантовой системы, совокупность обратных переходов — еѐ спектр испускания

При безызлучательных К. п. система получает или отдаѐт энергию при взаимодействии с др. системами. Например, атомы или молекулы газа при столкновениях друг с другом или

с электронами могут получать энергию (возбуждаться) или терять еѐ.

Три типа квантовых переходов

Излучательные квантовые переходы могут быть спонтанными ("самопроизвольными"), не зависящими от внешних воздействий на квантовую систему (спонтанное испускание фотона), и вынужденными, стимулированными

— под действием внешнего электромагнитного излучения резонансной частоты ν.

Важнейшей характеристикой любого К. п. является вероятность, определяющая, как часто происходит данный К. п. Вероятность перехода

измеряют числом переходов данного типа в

рассматриваемой квантовой системе за единицу Вынужденное испускание фотона времени (1 сек); поэтому она может принимать

любые значения от 0 до ω (в отличие от вероятности единичного события, которая <1)

Поглощение, cпонтанное и стимулированное излучение.

Для того, чтобы достичь необходимых и благоприятных условий, при которых возможно вынужденное излучение и, тем самым установить критерии для получения лазерного воздействия, важно проанализировать значения скоростей с которыми эти процессы должны произойти.

Основу для определения относительных скоростей этих процессов заложил Эйнштейн, определивший хорошо известные константы «А» и «В», ныне известные как коэффициенты Эйнштейна.

Коэффициент «А» относится к вероятности спонтанного излучения. Коэффициент «В» относится к вероятности вынужденного излучения и поглощения. Поглощение и вынужденное излучение – процессы аналогичные. Поэтому относительные скорости как поглощения, так и вынужденного излучения, зависят от населѐнности верхнего и нижнего уровней энергии соответственно. В качестве иллюстрации рассмотрим двухуровневую систему с более низким энергетическим уровнем 1 и находящимся выше более энергетически насыщенным уровнем 2, имеющими населѐнности N1 и N2, соответственно.

Коэффициенты Эйнштейна для трех процессов выглядят следующим образом: В12 (поглощения), А21 (спонтанное излучение) и B21 (вынужденное излучение). Нижние индексы для коэффициентов Эйнштейна здесь представляют направление перехода. Например, В12 - коэффициент Эйнштейна для перехода с уровня 1 на уровень 2. Кроме того, поскольку процессы поглощения и вынужденного излучения аналогичны, то в соответствии с законами

квантовой механики, B12 = B21.

Если E1 и E2 – энергии, соответствующие уровням 1 и 2, тогда населенность этих уровней может быть выражена уравнением, известным, как распределение Больцмана:

N2/N1 = exp [- (E2 - E1)/kT]

где k = 1.38×10-23 Дж×K-1 или 8.6×10-23 эВ×K-1 - постоянная Больцмана

T – абсолютная температура в градусах Кельвина