
- •Введение
- •1. История развития теории надежности
- •2. Надежность как прикладная научная дисциплина
- •3. Надежность и качество
- •4. Физико-химические процессы, влияющие на надежность
- •Влияние некоторых внешних воздействий на полупроводниковые приборы
- •5. Классификация основных состояний объекта
- •6. Номенклатура и классификация показателей надежности
- •Номенклатура показателей надежности
- •7. Количественные характеристики надежности технических устройств
- •7.1. Показатели безотказности невосстанавливаемых объектов
- •7.2. Показатели безотказности восстанавливаемых объектов
- •7.3. Показатели долговечности
- •7.4. Показатели ремонтопригодности
- •7.5. Показатели сохраняемости
- •7.6. Комплексные показатели надежности
- •7.7. Аналитические зависимости между показателями надежности
- •8. Нормирование показателей надежности
- •9. Моделирование и анализ надежности технических устройств и систем
- •9.1. Методология моделирования надежности
- •9.2. Методы анализа структурной надежности сложных технических систем (см. Также пз 2)
- •9.2.1. Основные типы структурных схем надежности Системы с последовательным соединением элементов
- •Системы с параллельным соединением элементов
- •9.2.2. Структурно-логический метод анализа системы
- •9.3. Вероятностные методы анализа надежности
- •9.3.1. Вероятностная модель внезапного отказа
- •9.3.2. Вероятностная модель постепенного отказа
- •9.4. Топологические методы
- •9.5. Принципы расчета надежности при проектировании
- •Обоснование норм надежности
- •Расчет надежности
- •Значения поправки для разных условий эксплуатации
- •Интенсивности отказов элементов радиоэлектронной аппаратуры
- •10. Методы повышения и обеспечения надежности
- •10.1. Методы повышения структурной надежности
- •Классификация способов резервирования элементов систем
- •10.2. Надежность систем при разных способах структурного резервирования
- •10.3. Обеспечение надежности при эксплуатации
- •Классификация ремонта
- •11. Испытания на надежность (определение надежности по экспериментальным данным)
- •11.1. Классификация испытаний и планов испытаний на надежность
- •Классификация испытаний технического объекта
- •Цели испытаний технических устройств
- •Планы испытаний на надежность
- •Рекомендуемые планы испытаний на надежность
- •11.2. Определительные испытания на надежность
- •Планирование испытаний
- •Определение объема испытаний для плана испытаний [nun]
- •Определение объема испытаний для плана [nUr]
- •Определение объема испытаний для плана [nuт]
- •Определение объема испытаний для планов [nMr], [nmt], [nRr], [nrt]
- •11.3. Оценка показателей надежности
- •11.3.1. Экспериментальные методы
- •Точечная оценка непараметрическим методом
- •Формулы для вычисления значений точечных оценок показателей надежности
- •Точечная оценка параметрическим методом
- •Формулы для вычисления значений точечных оценок показателей надежности при известном законе распределения
- •Точечные оценки параметра λ экспоненциального распределения
- •Интервальные оценки показателей надежности
- •Вычисление интервальных оценок показателей надежности непараметрическим методом
- •Экспоненциальное распределение
- •Распределение Вейбулла
- •Интервальные оценки показателей надежности
- •Оценка остаточного ресурса по результатам испытаний
- •Оценка показателей безотказности при испытаниях с измерением определяющих параметров
- •11.3.2. Расчетно-экспериментальные методы
- •Коэффициенты отношения параметров распределений
- •Типовые ситуации
- •Интервальная оценка вероятности безотказной работы систем с последовательной ссн при биномиальных испытаниях
- •Оценка показателей безотказности систем с последовательной ссн при планах испытаний с измерением наработки до отказа
- •Оценки параметра λ
- •Оценка показателей долговечности систем с последовательной ссн
- •Оценки среднего ресурса системы по ресурсу элементов
- •Оценка гамма – процентного ресурса системы
- •11.3.3. Контрольные испытания на надежность
- •Применяемость контрольных испытаний на надежность по гост 27.410-87
- •Метод одноступенчатого контроля
- •Контроль показателя безотказности Один контрольный уровень
- •Два контрольных уровня
- •Одноступенчатые планы контроля вероятности безотказной работы
- •Контроль наработки
- •Одноступенчатые планы контроля наработки
- •Метод многоступенчатого контроля
- •Метод последовательного контроля
- •Контроль безотказности
- •Контроль наработки
- •11.3.4. Контроль надежности сложных систем по данным о надежности их элементов
- •Объем испытаний для контроля вероятности безотказной работы при биномиальном плане
- •Объем испытаний для контроля наработки при экспоненциальном законе распределения
- •11.3.5. Методы ускоренных испытаний
- •12. Исследование риска
- •12.1. Методы анализа риска Стандарты, устанавливающие и использующие понятия риска и его оценок, а также относящиеся непосредственно к менеджменту риска:
- •Перечень наиболее распространенных методов, используемых при анализе риска (по гост р 51901.1-2002)
- •Перечень дополнительных методов, используемых при анализе риска
- •Исследование опасности и связанных с ней проблем (hazop)
- •Анализ видов и последствий отказов (fmea)
- •Анализ диаграммы всех возможных последствий несрабатывания или аварии системы (анализ «дерева неисправностей») (fта)
- •Анализ диаграммы возможных последствий события (анализ «дерева событий») (ета)
- •Предварительный анализ опасности (рна)
- •Оценка влияния на надежность человеческого фактора (hra)
- •12.2. Оценивание риска
- •Матрица риска
- •Матрица критичности отказов
- •12.3. Количественный анализ технического риска
- •Рекомендации по выбору методов анализа риска
- •Рассмотрим простой экспрессный метод количественного анализа риска
Интервальная оценка вероятности безотказной работы систем с последовательной ссн при биномиальных испытаниях
ПРИМЕР 31
Система
состоит из mпоследовательно соединенных элементов,
вероятность безотказной работы каждого
из которыхPiнеизвестна. Отказы элементов независимы.
Каждыйi-ый элемент
как бы проходитNiавтономных испытаний по биномиальному
плану, с регистрацией числа отказовli.
Испытания проходят в номинальном режиме
без остановок. По результатам испытаний
каждого элемента требуется найтиγ- нижнюю границу для вероятности безотказной работы
системы на интервале времени [0,t0],
т.е. для заданной доверительной вероятностиγдолжно выполняться неравенство:P(
для вероятности безотказной работы
системы на интервале времени [0,t0],
т.е. для заданной доверительной вероятностиγдолжно выполняться неравенство:P(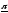 )≥γ.
)≥γ.
Даже при таких, упрощенных условиях, решение задачи неоднозначно. Рассмотрим один из вариантов решения:
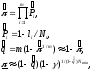
где Nmin– минимальное число испытаний из всехNi.
Пусть задано: m=3,Ni=10 (для всех элементов),li=2 (для всех элементов).γ=0,8.
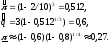
Оценка показателей безотказности систем с последовательной ссн при планах испытаний с измерением наработки до отказа
В данном случае известны план испытаний и вид закона распределения (или его класс) наработки до отказа i–того элемента. Из всех возможных ситуаций рассмотрим наиболее «определимую», а именно: все элементы испытываются по одному и тому же плану, закон распределения показателей безотказности для всех элементов один и тот же, неизвестны лишь его параметры, есть данные о наработках до отказа или цензурирования каждого из элементов системы.
По этим данным оценивают неизвестные параметры закона распределения наработки до отказа каждого элемента, а затем находят точечные и интервальные оценки вероятности безотказной работы системы с последовательной ССН.
Рассмотрим случай экспоненциального закона распределения наработки до отказа. При этом выберем наиболее простую систему – систему, состоящую из n последовательно соединённых однотипных элементов (типовая ситуация ТС-1). Вероятность безотказной работы такой системы определяется выражением:

Точечные и интервальные оценки вероятности безотказной работы системы находят по соотношениям:
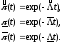
Точечные и интервальные оценки параметра Λ находят по формулам, приведённым в табл. 23.
Таблица 23
Оценки параметра λ
|
План испытаний |
Точечная
оценка
|
Доверительная граница |
Примечание | ||
|
нижняя |
верхняя | ||||
|
[NiUTi] |
|
|
|
| |
|
[NiUri] |
|
|
|
| |
|
[NiUzi] |
|
|
|
| |
Примечание: При одной группе однородных элементов ni= 1.
ПРИМЕР 32
Система состоит из последовательно соединенных однотипных элементов (типовая ситуация ТС-1). Вычислить оценки вероятности безотказной работы (точечную и доверительные границы при доверительной вероятности 0,9) при исходных данных:
- число последовательных элементов в системе n = 2;
- испытания элементов проведены по плану [NiUTi];
- для 1-го элемента проведено 5 испытаний до наработки 10 часов, зафиксировано 2 отказа после наработок 5 и 7 часов;
- для 2-го элемента проведено 8 испытаний до наработки 10 часов, зафиксировано 3 отказа после наработок 5, 6 и 9 часов;
- закон распределения экспоненциальный;
- наработка для оценки показателя надёжности t0= 10 часов.
S1=5+7+10(5-2)=42 часа, λ1=2/42=0,0476, S2=5+6+9+10(8-3)=70 часов, λ2=3/70=0,0429,
 =0,0476+0,0429=0,0905.
=0,0476+0,0429=0,0905.
Для q = 0,9 иdΣ= 2+3=5 по таблицам для квантилей χ2- распределения находим:

Оценки показателей безотказности систем с разнотипными элементами, другими типовыми ситуациями и иными законами распределения подробно рассмотрены в справочниках.













