ЛАБОРАТОРНАЯ РАБОТА № 6

ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПОЛЕЗНОЙ МОЩНОСТИ,

К.П.Д. ИСТОЧНИКА ТОКА И СИЛЫ ТОКА В ЦЕПИ ОТ НАГРУЗКИ

Цель работы - исследование зависимости полезной мощности, к.п.д. источника тока и силы тока в цепи от нагрузки.

Приборы и принадлежности: исследуемый источник тока, реостат, вольтметр, амперметр и ключ.

Краткие сведения из теории

При комнатной температуре (Т ≈ 300 К) электроны проводимости в металле можно рассматривать как классические частицы массой m и зарядом е, равномерно распределенные по объему проводника. Они находятся в постоянном хаотическом тепловом движении и взаимодействуют с атомами проводника только при столкновениях. Взаимодействием между электронами можно пренебречь. Движение электронов проводимости по объему проводника аналогично движению молекул газа, поэтому очень часто говорят, что электроны проводимости образуют в металле «электронный газ».

Так как движение электронов проводимости при отсутствии внешних полей хаотично, средняя скорость теплового движения электронов < u > равна нулю. Однако после включения внешнего однородного электрического поля напряженностью Е на электроны проводимости действует сила F = — еЕ, которая одинакова для всех электронов. Под действием этой силы электроны получают дополнительную ско­рость υ в противоположном вектору Е направлении (см. рис. 6.1). Среднее время τ, в течение которого электрон проводимости движется в поле Е между двумя столкновениями с ионами проводника, называется временем свободного пробега.

Рис. 6.1

Будем считать, что в результате столкновения с атомом металла электрон полностью теряет дополнительную скорость υ, которую он приобрел в электрическом поле.

Из классической теории электропроводности металлов следует, что удельное сопротивление проводника можно вы­числить по формуле

, (6.1)

где n — число электронов проводимости в единице объема.

Рассмотрим движение электрона проводимости после столкновения с атомом решетки проводника. В начальный момент его дополнительная скорость υ равна нулю. Ускорение, с которым движется электрон в электрическом поле, равно a = E.

Это значит, что за время свободного пробега дополнительная скорость электрона увеличится от 0 до величины υ_max:

υ_max = Eτ,

а его полная скорость составит u' = u + υ_max. В результате столкновения с атомом решётки проводника электрон теряет дополнительную скорость υ_max, увеличивая энергию колебаний атомов решетки. За время свободного пробега τ каждый электрон в среднем один раз сталкивается с атомами крис­таллической решетки и передает им энергию:

.

Общее количество энергии, которое получат атомы решетки за время τ, будет равно: , где V — объем проводника. Иначе говоря, полная мощность Р, рассеиваемая в проводнике, вычисляется по формуле

.

Она равна энергии, которую получают атомы проводника от электронов проводимости в единицу времени. Выразим мощ­ность Р, рассеиваемую во всем объеме проводника, исполь­зуя формулу (6.1), в следующем виде:

,

где j – плотность тока (j = E – закон Ома в дифференциальной форме).

Учитывая, что для цилиндрического проводника объем V = SL и падение напряжения U = EL, получим: (закон Джоуля - Ленца), где . Мощность, выделяемая в единице объема, вычисляется по формуле (закон Джоуля - Ленца в дифференциальной форме).

Таким образом, в рамках классической теории электропроводности получен закон Джоуля - Ленца. На основании предыдущего рассмотрения движения электронов в проводнике можно сделать следующий вывод. В рамках классической теории выделение тепла в проводнике при протекании по нему электрического тока объясняется увеличением энергии колебаний атомов решетки проводника в ре­зультате столкновений с электронами проводимости, уско­ренными в электрическом поле.

Рассмотрим цепь, состоящую из источника тока с внут­ренним сопротивлением R₀ и электродвижущей силой Э₀ (см. рис. 6.2) и резистора с переменным сопротивлением R.

Рис. 6.2

Сила тока в цепи

. (6.2)

Мощность, расходуемая во внешнем участке цепи, называется по­лезной мощностью источника тока, так как она может быть использо­вана для практических целей. Она равна

, (6.3)

где U — падение напряжения на внешнем сопротивлении R.

Полная мощность источника тока .

Коэф­фициент полезного действия источника тока

. (6.4)

С учетом формулы (6.2) и того, что U = IR, выражения для полезной мощности и к.п.д. примут следующий вид:

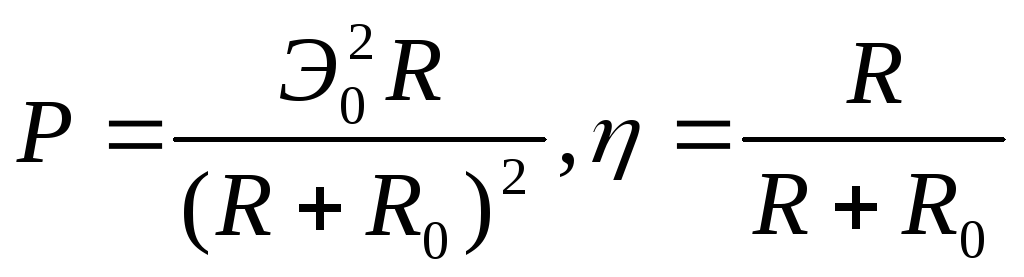. (6.5)

Исследование выражений (6.2) и (6.5) показывает, что требования получения максимального тока в цепи, максимальной полезной мощности и максимального к.п.д. противоречивы (см. рис. 6.3). Для получения возможно большего тока сопротивление нагрузки должно быть малым по сравнению с внутренним сопротивлением источника, но при этом близки к нулю полезная мощность и к.п.д.: почти вся совершаемая источником работа идет на выделение тепла во внутреннем сопротивлении. Чтобы получить максимальную полезную мощность, следует взять нагрузку с сопротивлением, равным внутреннему сопротивлению источника, но величина к.п.д. при этом составит только 0,5. Любую полезную мощность, меньшую максимальной, можно получить при двух значениях сопротивления нагрузки. В практических целях для получения заданной полезной мощности в этом случае следует выбирать нагрузку с большим сопротивлением, так как к.п.д. при этом выше.

Рис. 6.3

Описание экспериментальной установки

Схема установки представлена на рис.6.2. В цепь ис­точника постоянного тока включены реостат R, электроизме­рительные приборы (амперметр А и вольтметр V) и ключ К.

Порядок выполнения работы

1. Собрать схему, изображенную на рис.6.2.

2. Выбрать предел измерений по амперметру и записать в протокол наблюдений:

а) предел измерений амперметра в амперах;

б) число делений по шкале амперметра;

в) класс точности амперметра;

3. Повторить выбор предела измерений для вольтметра и записать в протокол наблюдений его параметры.

4. Изменяя сопротивление реостата R, снять отсчеты по амперметру и вольтметру, соответствующие каждому положению движка реостата (всего 15 точек). Результаты занести в таблицу (см. табл. 6.1).

5. Разомкнуть внешнюю цепь ключом К и измерить вольт­метром электродвижущую силу источника Э₀. Результат за­нести в протокол наблюдений.

Таблица 6.1

U		I (эксп.)		I (теор.), А	R, Ом	Р, Вт	η
дел.	В	дел.	А

Обработка и анализ результатов измерений

1. Вычислить значения полезной мощности источника Р по формуле (6.3), к.п.д. источника тока η — (6.4) и сопротивления R — по формуле . Результаты вычислений занести в таблицу (табл. 6.1).

2. Построить графики зависимостей P = P(R), η = η(R), I = I(R).

3. Определить ошибки измерения силы тока ΔI и напря­жения ΔU по формулам погрешности прямых измерений (с учетом класса точности приборов). Затем определить по­грешности измерения сопротивления внешней цепи ΔR, полезной мощности ΔР и к.п.д. источника Δη, используя формулы

4. Погрешности измерения силы тока, полезной мощности, к.п.д. и внешнего сопротивления отразить на графиках, по­строив на каждом прямоугольники ошибок для трех экспе­риментальных значений.

5. Вычислить величину внутреннего сопротивления источника, используя формулу для нескольких (пяти — шести) значений пар величин U и I. При расчете не следует использовать результаты измерений, соответству­ющие малым токам, так как при этом величина Э₀ — U мала и ошибка определения R₀ значительна. Усреднить полученные значения R_0.

6. Используя формулу (6.2), определить теоретические значения силы тока в цепи и на одном графике построить теоретические и экспериментальные зависимости силы тока I от внешнего сопротивления цепи R.

Контрольные вопросы

1. Каков механизм выделения тепла в проводнике при протекании по нему электрического тока?

2. Привести формулировки закона Джоуля - Ленца в интегральной и дифференциальной формах.

3. Сформулировать закон Ома для участка цепи, содержащего источник э.д.с., и для замкнутой цепи.

4. При какой величине внешнего сопротивления цепи полезная мощность источника тока максимальна (вывести)?

Библиогр.: [2] гл. VIII, § 8.5; гл. IX, §§ 9.2, 9.3; [6] гл. V, §§ 34, 35, 37, 38.