
Балтийский Государственный Технический Университет
«ВОЕНМЕХ», Имени Д.Ф.Устинова
Лабораторная работа № 1 «Определение орбиты по двум фиксированным положения методом Ламберта-Эйлера»
Работу выполнил:
студент группы А-591
Проверил:
Санников В. А.
Санкт-Петербург,
2012
Определение орбиты по двум фиксированным положениям методом Ламберта-Эйлера
1.Описание метода
Метод Ламберта-Эйлера
предназначен для определения параметров
орбиты перелета за время ![]() между начальным и конечным положениями
КА, заданными радиусами-векторами
между начальным и конечным положениями
КА, заданными радиусами-векторами ![]() и угловой дальностью Φ
(рис.1.1)
и угловой дальностью Φ
(рис.1.1)
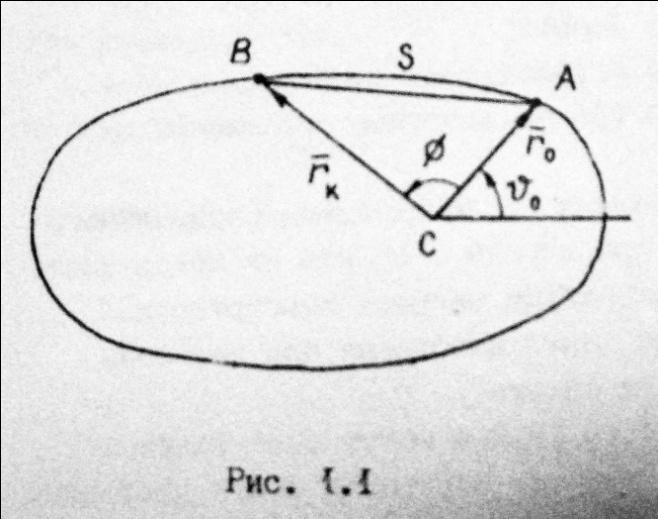
Итак, пусть
задан начальный радиус-вектор ![]() =
= ![]() , конечный радиус-вектор
, конечный радиус-вектор ![]() =
= ![]() , угловая дальность полета Φ
(угол АСВ) и время полета
, угловая дальность полета Φ
(угол АСВ) и время полета ![]() из точки А в точку В. Требуется определить
параметры орбиты перелета: р – фокальный
параметр; е – эксцентриситет орбиты;
из точки А в точку В. Требуется определить
параметры орбиты перелета: р – фокальный
параметр; е – эксцентриситет орбиты;
d – большая полуось.
Для расчета параметров орбиты методом Ламберта-Эйлера используется следующий алгоритм [1 -3].
1. Определяется расстояние между начальной и конечной точками полета:
S
= ![]() =
= ![]() .
.
2. Вычисляется
время перелета между заданными векторами
в предположении, что орбита является
параболической: ![]() где μ
– гравитационная постоянная.
где μ
– гравитационная постоянная.
3. Определяется
тип орбиты. Если ![]() >
>
![]() ,
то перелет может быть реализован только
по эллиптической орбите. Если
,
то перелет может быть реализован только
по эллиптической орбите. Если ![]() <
<
![]() ,
то перелет между заданными радиусами-векторами
возможен только по гиперболической
орбите.
Если же
,
то перелет между заданными радиусами-векторами
возможен только по гиперболической
орбите.
Если же ![]() =
=
![]() ,
то перелет между заданными векторами
должен производиться по параболической
траектории.
,
то перелет между заданными векторами
должен производиться по параболической
траектории.
4. Если перелет происходит по эллиптической орбите, то большая полуось эллипса α определяется из решения следующего трансцендентного уравнения (формула Ламберта):
![]() , (1.1)
, (1.1)
где ![]() ;
;
Sign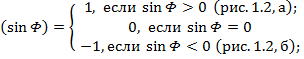
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
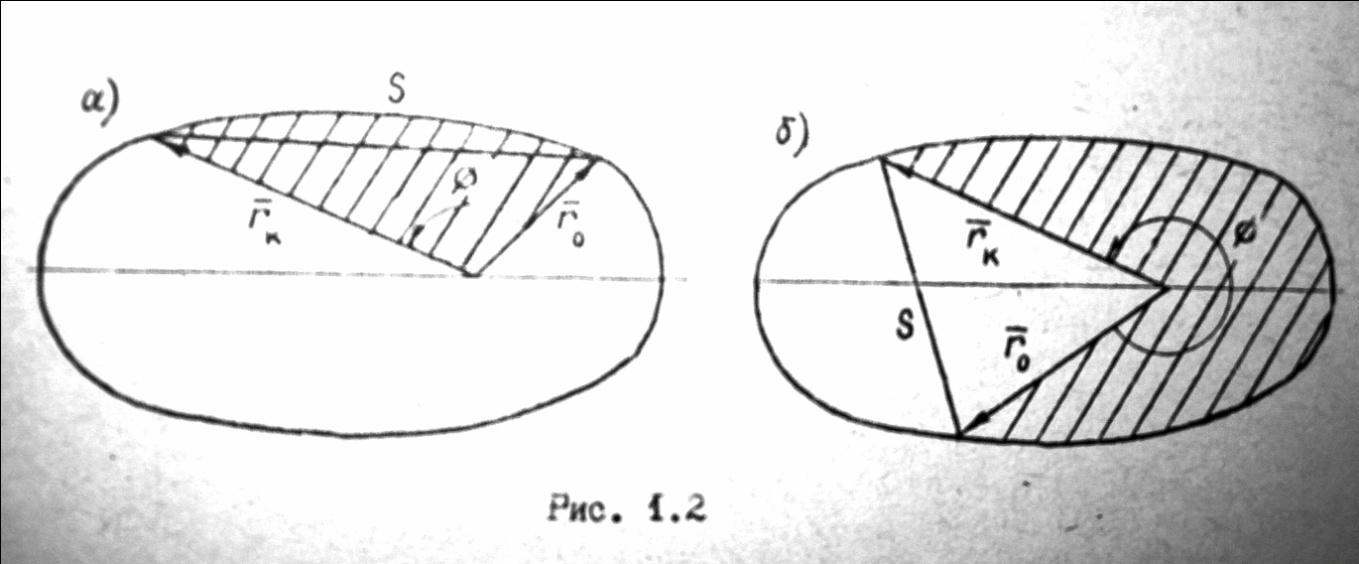
Если перелет проходит по гиперболической орбите, то большую полуось орбиты находят из решения следующего трансцендентного уравнения:
![]() (1.2)
(1.2)
Где
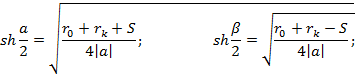
причем ![]()
Трансцендентные уравнения (1.1) и (1.2) решаются численно на ЭВМ с использование итерационного метода.
5. После
нахождения большой полуоси перелетной
орбиты ![]() вычисляется фокальный параметр
вычисляется фокальный параметр ![]() и эксцентриситет орбиты
и эксцентриситет орбиты ![]()
Из уравнения орбиты, записанного для начальной и конечной точки траектории, можно получить соотношения
![]()
Добавив к ним
уравнение орбиты ![]() ,
получим выражения для искомых параметров:
,
получим выражения для искомых параметров:
для эллиптической орбиты:
![]() (1.3)
(1.3)
![]()
для гиперболической орбиты:
![]() (1.4)
(1.4)
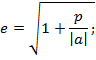
для параболической орбиты:
![]() (1.5)
(1.5)
![]()
При выполнении лабораторной работы трансцендентные уравнения решаются методом последовательных приближений.
А. Задают
минимальное ![]() и максимальное
и максимальное ![]() значения полуоси
значения полуоси ![]()
Для эллиптической орбиты принимают:
![]() (1.6)
(1.6)
![]()
Для гиперболической орбиты выбирают
![]()
(1.7)
![]()
Б. Вычисляют значения функции невязки
![]() =
= ![]() -
- ![]() (α)
(1.8)
(α)
(1.8)
для двух значении
α, т.е. ![]() =
= ![]() и
и ![]() =
= ![]() ,
причем для эллиптической траектории
,
причем для эллиптической траектории
![]() вычисляют по формуле (1.1), а для
гиперболической по формуле (1.2).
вычисляют по формуле (1.1), а для
гиперболической по формуле (1.2).
В. Новое
значение полуоси ![]() определяют методом хорд [4]:
определяют методом хорд [4]:
![]() =
= ![]() -
- ![]() ∙ (
∙ (![]() )
(1.9)
)
(1.9)
При использовании
(1.9) предполагается, что ![]() ∙
∙ ![]() < 0.
< 0.
Г. Вычисляют
![]() .
.
Д. Если ![]() = 0, то
= 0, то ![]() =
= ![]() .
В противном случае определяют новый
диапазон изменения
.
В противном случае определяют новый
диапазон изменения ![]() : принимают
: принимают ![]() =
=
![]() ,
если
,
если ![]() ∙
∙ ![]() < 0;
< 0;
или ![]() =
=
![]() ,
если
,
если ![]() ∙
∙ ![]() ≥ 0 ; и переход к новой итерации.
≥ 0 ; и переход к новой итерации.
Итерации
продолжают до тех пор, пока ![]() не станет меньше некоторой допустимой
величины β.
не станет меньше некоторой допустимой
величины β.
