лекции_ дисретной математики / ДМ(л14) / Лекция 15
.docЛекция 14
-
Пересечение графов
-
Соединение графов
-
Лемма о рукопожатиях
-
Список смежности
-
Вектор дерева
Пересечение графов
Пусть
и
– произвольные графы. Пересечением
графов
и
называется граф
со множеством вершин
и множеством ребер
.
Операция пересечения графов обладает следующими свойствами, которые следуют из определения операции и свойств операции пересечения множеств:
-
для любых графов
и
– свойство коммутативности; -
для любых графов
,
,
– свойство ассоциативности.
Для того чтобы
операция пересечения была всеобъемлющей,
необходимо ввести понятие пустого
графа. Граф G
называется пустым,
если его множество вершин пусто. Заметим,
что в этом случае множество ребер графа
также пусто. Пустой граф обозначается
символом
Пустой граф может быть получен в
результате выполнения операции
пересечения графов, у которых множества
вершин, а следовательно и множества
ребер, не пересекаются. Операция
пересечения графов распространяется
на любое конечное число графов по
индукции:
.
Операция пересечения графов может быть выполнена в матричной форме.
Теорема 1.
Пусть
и
– два графа (ориентированные или
неориентированные одновременно), и
пусть
и
– матрицы смежности вершин этих графов.
Тогда матрицей смежности вершин графа
является матрица А, полученная поэлементным
взятием минимума вспомогательных матриц
и
.
Матрицы
,
i=1,
2, получаются из
с помощью удаления строк и столбцов,
соответствующих вершинам, не вошедшим
в
.
Следствие.
Если элементы матриц смежности вершин
и
графов
и
принимают только значение 0 и 1, то
операция взятия минимального элемента
для нахождения матрицы смежности вершин
графа
соответствует логическому (обычному)
произведению элементов.
П
ример
1. На
рис. 1 представлены графы
,
и их пересечение
.
Рис 1
Составим матрицы смежности вершин исходных графов.
,
.
Находим множество
вершин результирующего графа:
Составим матрицы
смежности вершин вспомогательных графов
и
.
,
.
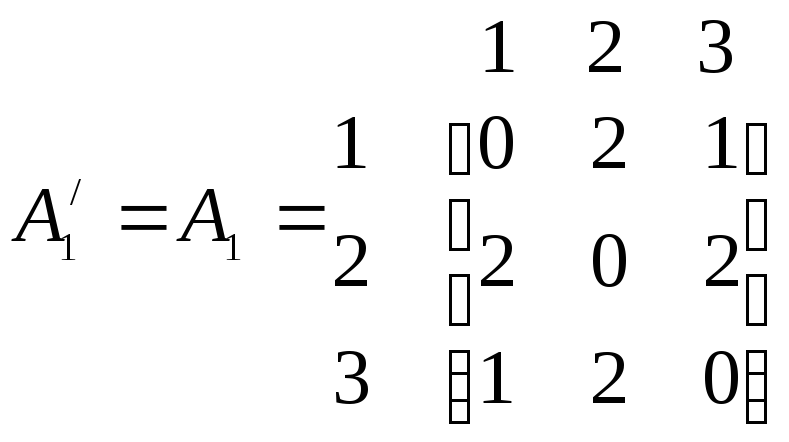Найдем матрицу смежности вершин графа G.
.
Полученная матрица смежности вершин А соответствует графу G, изображенному на рис.1.
Соединение графов
Эта операция была
введена А.А. Зыковым. Пусть
и
– два одновременно неориентированных
или ориентированных графа с непересекающимися
множествами вершин. Соединение
графов
состоит из
и всех ребер в случае неориентированного
графа (пар нестрого параллельных дуг в
случае орграфа), соединяющих
и
.
В частности,
,
по определению полного двудольного
графа. Эта операция иллюстрируется на
рис. 2, где
и
.
Рис. 2
Операция соединения графов обладает следующими свойствами, которые следуют из определения и свойств операции объединения:
-
для любых графов
и
– свойство коммутативности; -
для любых графов
,
,
– свойство ассоциативности.
Операцию соединения можно распространить на любое конечное число графов, все множества вершин которых различны:
G1+…+Gn–1+Gn=(G1+…+Gn–1)+Gn.