10
2 |
1 |
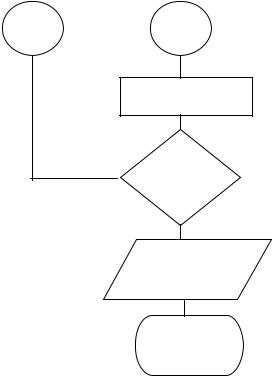
y1 = y
да
D > d нет нет
Вывод x, y
Конец
Рис. 2.6. Окончание
2.3. Сложные циклы
Вычислительные процессы, содержащие два или более включенных друг в друга циклов, называют сложными циклическими процессами (алгоритмами). Цикл, который содержит внутри себя другой цикл, называют внешним в противоположность внутреннему (вложенному). Необходимо учитывать, что за одно исполнение внешнего цикла внутренний цикл повторяется многократно.
Пример 5. Составить алгоритм вычисления и вывод на печать функции y = x*z / (A + B) при изменении аргументов 1≤ x ≤ 10 c шагом ∆x = 2 и 1≤ z ≤4 с шагом ∆z = 0.5.
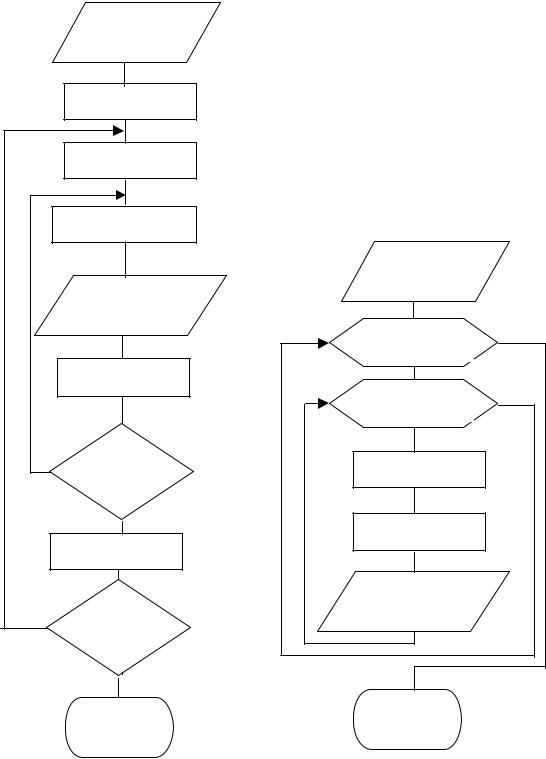
Решение данного примера показано на рис. 2.7. Внутренний цикл организован по переменной z , а внешний – по переменной x . На каждом шаге изменения переменной x (переменной внешнего цикла) переменная z (переменная внутреннего цикла) проходит весь заданный диапазон изменения от 1 до 4 с шагом 0.5. Блок вывода на печать помещен во внутреннем цикле, что позволяет регистрировать переменные во всем диапазоне их изменения. На рис. 2.8 эта же задача решена с помощью модифицированной блок-схемы алгоритма. В ней циклы представлены с помощью более компактных условных обозначений, принципы организации которых становятся ясными из рис. 2.9. Первая цифра внутри фигуры (рис. 2.9) определяет начальное значение переменной, вторая –
11
ее конечное значение, а третья – шаг изменения переменной. По умолчанию (при отсутствии последней цифры) шаг изменения переменной принимается равным 1.
Ввод A,B |
x = 1 |
z = 1 |
y = x*z /(A+B) |
Вывод x,y,z |
z=z+0.5 |
z ≤ 4 |
x = x + 2 |
x ≤10 |
Конец |
Рис. 2.7 |
Ввод A,B
x = 1,10,2 |
z = 1,4,0.5 |
y = x*z /(A+B) |
y1 = y |
Вывод x,z,y |
Конец |
Рис. 2.8 |
12
|
|
Вход в цикл |
|||
Вход i+1 |
|
|
|
|
|
|
|
|
|
|
|
|
X = 1,10,2 |
||||
шага цикла |
|
|
|
|
Выход из |
|
|
|
|
|
цикла |
Выход i-го шага цикла
Рис. 2.9
2.4. Алгоритмы с массивами
Наряду с одиночными переменными в задачах часто используются организованные переменные – массивы. Под массивом понимают совокупность данных, имеющих общее имя. По способу организации чаще всего различают одномерные и двумерные массивы. Одномерный массив – вектор, элементы которого снабжаются одним индексом, определяющим их порядковый номер в массиве. Двумерный массив – это матрица. Элементы одного массива снабжаются двумя индексами, первый из которых определяет номер строки, а второй – номер столбца. На пересечении номера строки и номера столбца расположен искомый элемент. Например, в массиве
A(2,2) = |
|
а11 |
а12 |
|
|||
|
а21 |
а22 |
элемент а11 расположен на пересечении первой строки и первого столбца, элемент а12 – на пересечении первой строки и второго столбца, элемент а21 – на пересечении второй строки и первого столбца и т. д. Элементы массива называются переменными с индексами или индексными переменными.
Пример 6. Составить алгоритм вычисления элементов массива Y(10) по элементам массива X(10), если
|
xi + а |
|||
уi ,j = |
|
|
|
. |
√ |
|
|
||
|
xi2 + 1 |
|
||
Алгоритм решения данной задачи приведен на рис. 2.10. В нем показано, что после блоков ввода переменной а и массива X(10) организуется цикл по индексной переменной i для вычисления элементов массива уi по элементам массива xi
.
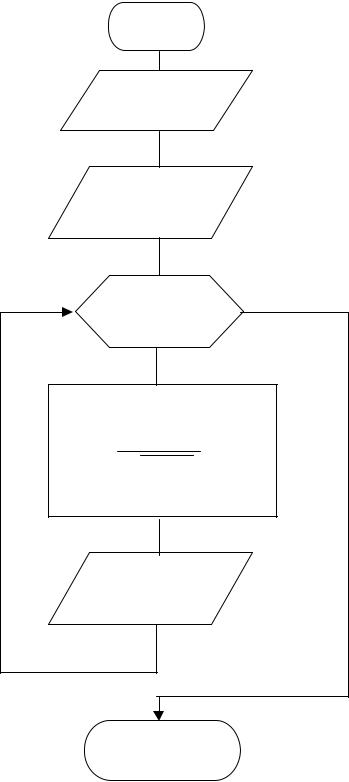
13
Начало
Ввод а
Ввод массива
X(10 )
i = 1,10,1
xi + а
yi =
√ xi2 + 1
Вывод yi
Конец
Рис. 2.10
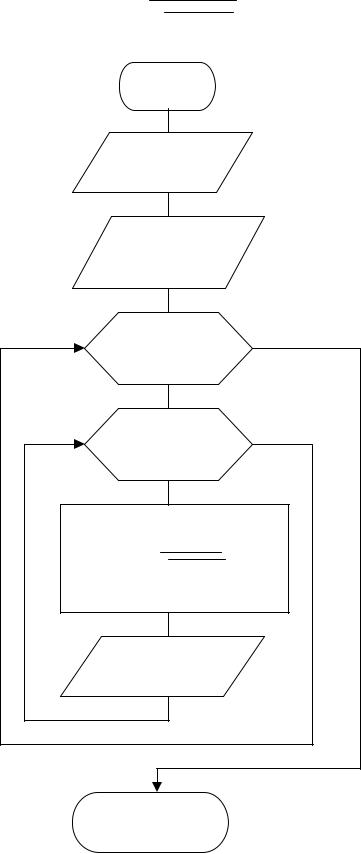
14
Пример 7. Составить алгоритм получения элементов массива Y(5,4) по элементам массива X(5,4), если
|
xi, j + a |
|
|
yi, j = |
. |
|
√ xi2, j + 1 |
|
. |
Начало |
|
|
|
|
|
Ввод а |
|
|
Ввод массива |
|
|
X(5,4} |
|
|
i = 1,5,1 |
|
|
j =1,4,1 |
|
|
xi + a |
|
|
yi, j = |
|
|
√ xi2, j + 1 |
|
|
Вывод yi,j |
|
|
Конец |
|
|
Рис. 2.11 |
. |
15
Алгоритм решения задачи из примера 7 приведен на рис. 2.11. Он отличается от предыдущего алгоритма наличием второго цикла по переменной j, так как адрес каждого элемента двумерного массива определяется двумя индексами.
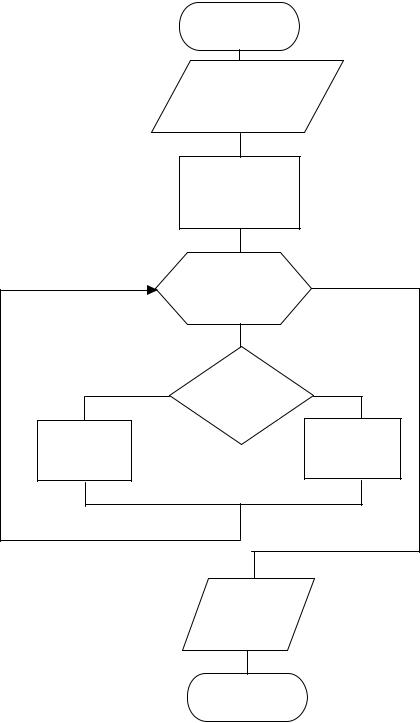
Пример 8. Дан массив ненулевых элементов А(10). Необходимо определить количество положительных и отрицательных элементов.
Пусть Р – количество положительных элементов, а Q – количество отрицательных элементов, тогда алгоритм решения задачи будет иметь вид, показанный на рис. 2.12.
|
Начало |
|
Ввод массива |
|
А(10 ) |
|
P = 0 |
|
Q = 0 |
|
i = 1,10,1 |
да |
нет |
|
аi>0 |
P=P+1 |
Q=Q+1 |
|
Вывод |
|
P, Q |
Конец
Рис. 2.12
16
Принцип работы данного алгоритма ясен из блок-схемы, однако надо иметь в виду, что перед входом в цикл необходимо выполнить обнуление переменных P и Q. В этих переменных формируются суммы по количеству положительных и отрицательных элементов, которые должны быть равны нулю перед входом в цикл.
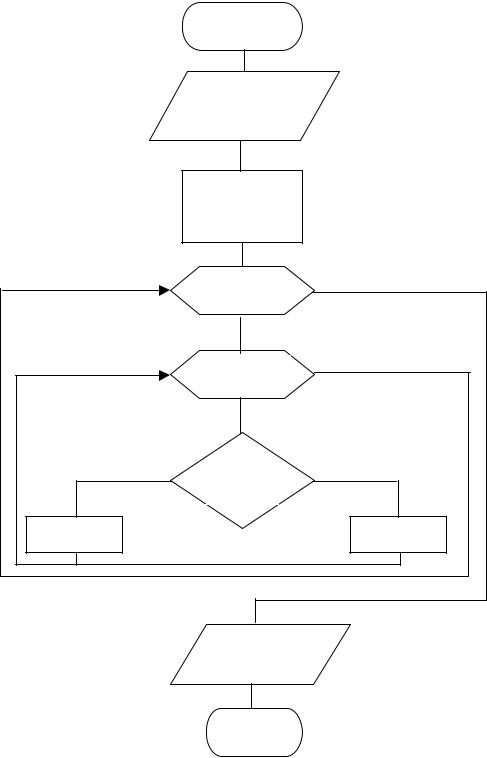
Пример 9. Задан массив ненулевых элементов В(2,3). Определить количество положительных и отрицательных элементов.
|
Начало |
|
Ввод мас- |
|
сива В(2,3) |
|
P = 0 |
|
Q = 0 |
|
i = 1,2,1 |
|
j = 1,3,1 |
да |
нет |
|
bi,j >0 |
P = P+1 |
Q = Q+1 |
Вывод P,Q
Конец
Рис. 2.13