5
2. Классификация алгоритмов
По типу используемого вычислительного процесса различают линейные (прямые), разветвляющиеся и циклические алгоритмы.
Линейные алгоритмы описывают линейный вычислительный процесс, этапы которого выполняются однократно и последовательно один за другим. Он включает последовательное выполнение следующих этапов:
-ввод исходных данных в память ЭВМ;
-вычисление искомых величин по формулам;
-вывод результатов из памяти ЭВМ на информационный носитель.
Пример 1. Составить алгоритм вычисления площади круга по формуле S = π R2. Решение показано на рис. 2.1.
Начало
Ввод R
S = πR2
Вывод S
Конец
Рис. 2.1
Разветвляющийся алгоритм описывает вычислительный процесс, реализация которого происходит по одному из нескольких заранее предусмотренных направлений. Направления, по которым может следовать вычислительный процесс, называются ветвями. Выбор конкретной ветви вычисления зависит от результатов проверки выполнения некоторого логического условия. Результатами проверки являются: “ истина” (да), если условие выполняется, и “ ложь ” (нет), при невыполнении условия.
6
Пример 2. Составить алгоритм решения для функции F(x) = 1 при x > 0 и F(x) = 0 при x ≤ 0. Блок – схема разветвляющегося алгоритма показана на рис. 2.2.
Начало
Ввод x
x >0
F = 0 |
|
|
F = 1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вывод F
Конец
Рис.2.2
Циклический алгоритм описывает вычислительный процесс, этапы которого повторяются многократно. Различают простые циклы, не содержащие внутри себя других циклов, и сложные (вложенные), содержащие несколько циклов. В зависимости от ограничения числа повторений выделяют циклы с известным числом повторений и циклы, число повторений которых заранее неизвестно.
2.1. Циклы с известным числом повторений
При организации этих циклов присутствуют стандартные элементы, сопровождающие любой цикл:
7
-подготовка первого выполнения цикла (присвоение счетчику цикла начального значения);
-тела цикла, которое образуют блоки , выполняемые многократно;
-изменение значения счетчика циклов и сравнение его с конечным значением. Блок-схемы циклических алгоритмов существенно отличаются структурами
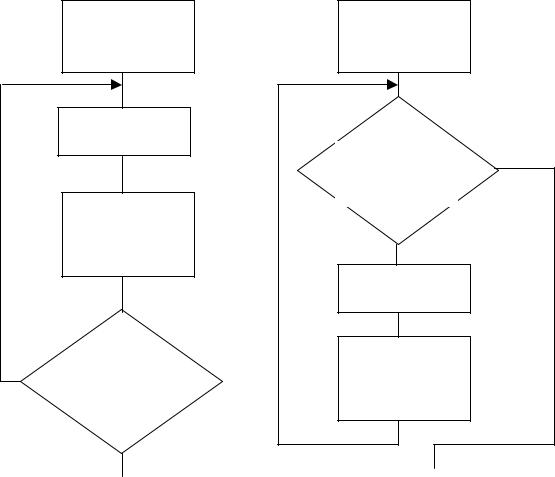
повторения “повторять ДО ”(повторять до выполнения условия окончания цикла) или “повторять ПОКА ” (повторять пока выполняются условия продолжения циклического процесса). В первом варианте проверка условий окончания циклических вычислений осуществляется в конце цикла (рис. 2.3, а), а во втором – в начале цикла (рис. 2.3, б). Как видно из рисунка, цикл “повторять ДО ”выполняется, по крайней мере, один раз, а цикл “повторять ПОКА”может сразу привести к выходу из цикла.
|
Подготовка вы- |
Подготовка вы- |
|
|
полнения пер- |
полнения пер- |
|
|
вого цикла |
вого цикла |
|
|
Тело цикла |
|
|
|
|
Условие |
да |
|
|
|
|
|
|
окончания |
|
|
Подготовка |
|
|
|
выполнения |
нет |
|
|
следующего |
|
|
|
цикла |
Тело цикла |
|
|
|
|
|
|
|
Подготовка вы- |
|
|
Условие |
полнения сле- |
|
нет |
окончания |
дующего |
|
|
цикла |
|
|
|
да |
|
|
|
а) |
б) |
|
|
|
Рис. 2.3 |
|
Пример 3. Составить алгоритм решения задачи вычисления N первых членов геометрической прогрессии, используя формулу bn+1 = bn *q для любых b и q, где n – текущий член геометрической прогрессии.
8
Блок-схема алгоритма решения данного примера показана в двух вариантах: с использованием цикла “ДО” (рис. 2.4, а) и цикла “ПОКА”( рис. 2.4, б).
Ввод b,q,N |
Ввод b,q,N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
n=1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
b = b*q |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
n≤N |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
да |
||||
|
|
Вывод b |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b = b*q |
|
|
||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
n = n +1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Вывод b |
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
нет |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
n > N |
|
|
|
|
n = n +1 |
|
||||||
|
|
|
||||||||||||
|
|
|
|
|
да |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Конец |
|
|
|
|
Конец |
||||||
|
|
|
|
|
a) |
|
|
|
|
|
б) |
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
Рис. 2.4
2.2. Циклы с неизвестным числом повторений
Примером циклов, число повторений которых не задано, являются итерационные вычислительные процессы. В них решение задачи реализуется путем последовательного приближения к искомому результату. Процесс является циклическим, поскольку заключается в многократных вычислениях. Начальное приближение Y0 выбирается заранее или задается по определенным правилам. Заканчивается итерационное вычисление при выполнении условия
Yi – Yi – 1 ≤ d ,
где d – допустимая ошибка вычисления.
9
Типовая структура алгоритма итерационных вычислений имеет вид, показанный на рис. 2.5.
|
|
|
|
|
|
Задание начальных |
|
Y1=Y(0) |
|||||
|
условий |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y= f(Y1) |
Первая итерация |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D = Y- Y1 |
|
|
Вычисление текущей |
||
|
|
|||||
|
|
|
|
|
|
ошибки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y1= Y |
Переприсвоение |
||||
|
|
|
|
|
|
|
D ≤ d |
Оценка точности |
нет
да
Рис. 2.5
Пример 4. Составить алгоритм вычисления функции y = √ x c точностью d, используя рекуррентную формулу yi+1 = 0.5 (x / yi + yi )
Если начальное приближение y1 = x , тогда на первом цикле вычисления будем иметь y = 0.5 (x / y1 + y1) Блок - схема алгоритма решения примера 4 приведена на рис. 2.6.
Ввод x , d
y1= x
y=0.5(x/y1 +y1 )
D = y - y1
2 |
1 |
Рис. 2.6