Логические базисы и-не, или-не
Булевый базис не является единственной функционально полной системой логических функций. Среди других наибольшее распространение получили базис И-НЕ и базис ИЛИ -НЕ.
Чтобы доказать логическую полноту любого базиса, достаточно показать, что в этом базисе можно реализовать базовые функции И, ИЛИ, НЕ.
Для базиса И-НЕ в качестве базового элемента используется элемент приведенный на рисунке рис.1.2.10,а.
a
b
Рис. 1.2.9
Реализация с помощью функции И-НЕ базовых функций алгебры Буля осуществляется следующим образом.
ИЛИ:
И:
Функция НЕ реализуется с помощью схемы И -НЕ с одним входом.
На рис.1.2.11 риведена схемная реализация функций И, ИЛИ, НЕ в базисе И - НЕ.
Рис. 1.2.10
Реализация с помощью логической функции ИЛИ-НЕ базовых функций алгебры Буля осуществляется следующим образом.
ИЛИ:
И:
Функция НЕ реализуется с помощью схемы ИЛИ -НЕ с одним входом.
На рис.1.2.12 приведена схемная реализация операции И, ИЛИ, НЕ в базисе ИЛИ – НЕ
И
ИЛИ НЕ
Рис. 1.2.11.
При синтезе логических схем в заданном базисе логических элементов (например, в базисе И-НЕ, или ИЛИ - НЕ) целесообразно предварительно исходное выражение привести к форме, в которой в выражении будут использованы только логические операции, соответствующие используемым логическим элементам в заданном базисе.
Пример
Синтезировать логическую схему в базисе И - НЕ, соответствующую выражению
.
Решение
Используя правило де Моргана преобразуем исходное выражение таким образом, чтобы последней операцией было отрицание и в выражение были бы только операции И.
Полученное выражение, представленное в виде вложенных операции И-НЕ, позволяет синтезировать соответствующую логическую схему в заданном базисе, которая приведена на рис.1.2.13.
Рис. 1.2.12
Пример
Синтезировать логическую схему в базисе ИЛИ - НЕ, соответствующую выражению
Решение
Используя правило де Моргана преобразуем исходное выражение таким образом, чтобы последней операцией было отрицание и в выражение были бы только операции ИЛИ.
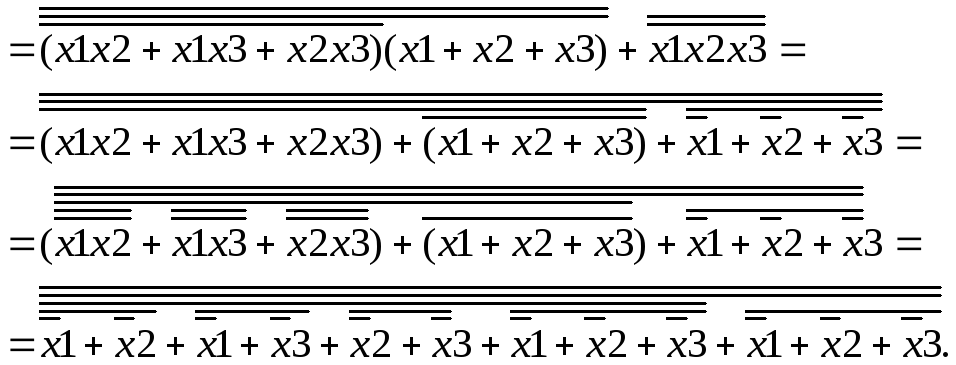
Полученное выражение, представленное в виде вложенных операций ИЛИ-НЕ, позволяет легко синтезировать соответствующую логическую схему в заданном базисе, которая приведена на рисунке рис.1.2.14.
Рис. 1.2.13