10.2. Логические базисы и–не, или–не

Булевый базис не является единственной функционально полной системой логических функций. Среди других наибольшее распространение получили базис И–НЕ и базис ИЛИ–НЕ.

Чтобы доказать логическую полноту любого базиса, достаточно показать, что в этом базисе можно реализовать базовые функции И, ИЛИ, НЕ.

Для базиса И-НЕ в качестве базового элемента используется элемент приведенный на рисунке рис. 2.5,а.

y =

___

=x₁x₂

x₁

х₂

x₁

x₂

y =

_____

=x₁+ x₂

&

1

а б

Рис. 2.5. Базовые элементы: а – И–НЕ;б– ИЛИ–НЕ

Реализация с помощью функции И-НЕ базовых функций алгебры Буля осуществляется следующим образом.

ИЛИ: _;

И:

Функция НЕ реализуется с помощью схемы И-НЕ с одним входом.

На рис. 2.6. приведена схемная реализация функций И, ИЛИ, НЕ в базисе И-НЕ.

y=x₁+х ₂

x₁

х₂

&

&

y= x₁

&

x₁

y=x₁*х₂

x₁

x₂

&

&

ИЛИ И НЕ

а б в

Рис. 2.6. Реализация булевых функций в базисе И–НЕ: а – функция ИЛИ; б – функция И; в – функция НЕ

Реализация с помощью логической функции ИЛИ-НЕ базовых функций алгебры Буля осуществляется следующим образом.

ИЛИ: _;

И:

Функция НЕ реализуется с помощью схемы ИЛИ-НЕ с одним входом.

Н

x₁

x₂

а рис.2.7. приведена схемная реализация операций И, ИЛИ, НЕ в базисе ИЛИ-НЕ

y =

= x₁+х₂

y=

_

=x₁

x₁

х₂

1

1

1

1

x₁

y = x₁.х₂

1

И ИЛИ НЕ

абвв)

Рис. 2.7. Реализация булевых функций в базисе ИЛИ–НЕ: а – функция И; б – функция ИЛИ; в – функция НЕ

10.3.Синтез логических схем в базисах И–НЕ, ИЛИ–НЕ

При синтезе логических схем в заданном базисе логических элементов (например, в базисах И–НЕ, или ИЛИ–НЕ) целесообразно предварительно исходное выражение привести к форме, в которой в выражении будут использованы только логические операции, соответствующие используемым логическим элементам в заданном базисе.

Пример

Синтезировать логическую схему в базисе И–НЕ, соответствующую выражению

.

Решение

Используя правило де Моргана преобразуем исходное выражение таким образом, чтобы последней операцией было отрицание и в выражение были бы только операции И.

Полученное выражение, представленное в виде вложенных операции И-НЕ, позволяет синтезировать соответствующую логическую схему в заданном базисе, которая приведена на рис.2.8.

x₁x₂x₃

&

y

&

&

&

&

&

&

&

&

&

Рис. 2.8. Реализация логического выражения в базисе И–НЕ

Пример

Синтезировать логическую схему в базисе ИЛИ-НЕ, соответствующую выражению

Решение

Используя правило де Моргана, преобразуем исходное выражение таким образом, чтобы последней операцией было отрицание и в выражение были бы только операции ИЛИ.

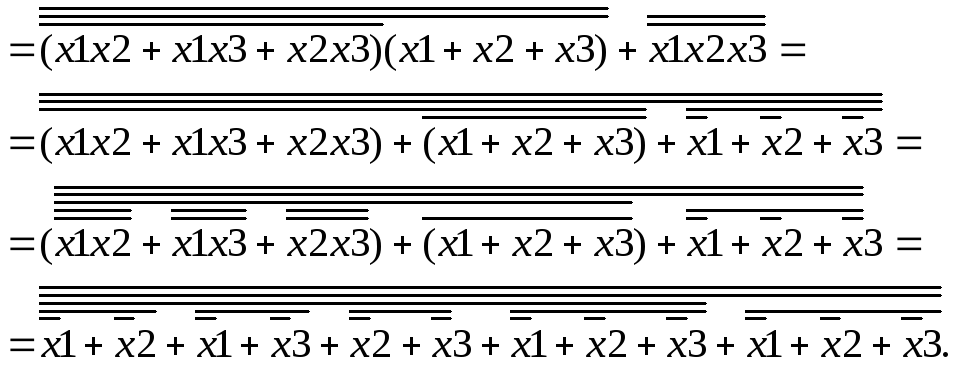
Полученное выражение, представленное в виде вложенных операций ИЛИ-НЕ, позволяет легко синтезировать соответствующую логическую схему в заданном базисе, которая приведена на рисунке рис. 2.9.

x₁ x₂x₃