19 Статистическая проверка гипотез

Под статистической гипотезой (или просто гипотезой) понимают всякое высказывание (предположение) о генеральной совокупности, проверяемое по выборке.

Статистические гипотезы делятся на гипотезы о параметрах распределения известного вида (параметрические гипотезы) и гипотезы о виде неизвестного распределения (непараметрические гипотезы).

Одну из гипотез выделяют в качестве основной (или нулевой) , а другую, являющуюся логическим отрицанием— в качествеконкурирующей (или альтернативной) гипотезы .Процедура проверки соответствия высказанного предположения (гипотезы) с выборочными данными называетсяпроверкой гипотезы.

Правило, по которому принимается решение принять или отклонить гипотезу , называетсястатистическим критерием (или просто критерием) проверки гипотезы .

Применение статистических критериев проверки нулевой гипотезы основывается на специально подобранной СВ – выборочной статистике, характеризующей меру расхождения между теоретическим и эмпирическим распределением. Часто саму СВ называют статистическим критерием или критической статистикой.

Критерием согласия называют статистический критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Одним наиболее распространённым критерием проверки непараметрических гипотез о виде функции распределения изучаемой случайной величины является критерий(Пирсона). Данный критерий проверяет гипотезу о возможном законе распределения и применяется для разных распределений.

Схема применения критерия для проверки гипотезыо законе распределения изучаемой случайной величинызаключается в следующем:

1. Рассматриваем гипотезу Н₀ о законе распределения случайной величины (дискретной или непрерывной);

2. По выборке находим оценки инеизвестных параметров предполагаемого закона распределения;

3. Определяем частоты , с которымивстречаются в выборке значениядискретной СВ или выборочные значения непрерывной СВ, принадлежащие соответствующим интервалам;

4. Находим теоретические вероятности − для дискретной СВ,− для непрерывной, в частности, для нормального закона распределения имеем

;

5. Вычисляем наблюдаемое значение критической статистики критерия −:;

6. Контроль вычислений осуществляется равенством.

7) Принимаем статистическое решение: гипотеза Н₀ не противоречит выборке наблюдений на данном уровне значимости , если, где− число степеней свободы, а− число параметров распределения. Если же, то гипотезаН₀ отклоняется и может быть выдвинута другая гипотеза Н₁, которая проверяется по той же схеме[3-5].

25.Симплекс метод

1 Этап. Построение первоначального базисного плана.

Рассмотрим ЗЛП в канонической форме. Предположим, что среди векторов условий найдутсялинейно независимых единичных векторов (единичный базис). Соответствующие им переменные (компоненты вектора) назовембазисными, а оставшиеся − небазисными переменными. Пусть далее , т.е.. Не ограничивая общности, предполагаем, что базисными являются первыепеременных. Тогда ЗЛП приобретает вид.при ограниченияхЗначения небазисных переменных принимаем равными нулю, тогда из (11) вытекает, чтои получим первоначальный базисный план вида. Если задача задана в нормальной форме и, то всегда легко найти первоначальный базисный план, переходя к канонической форме. За единичный базис нужно взять векторы, соответствующие свободным переменным.При решении ЗЛП симплекс-методом удобно пользоваться симплексными таблицами (таблица 1), которые составляются для каждого плана.Последнюю, (m+1)−ю строку симплексной таблицы называют индексной строкой. 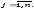В нее заносят значение целевой функции для начального опорного плана и оценкивекторов условий:,Оценки базисных векторов всегда равны нулю.