
- •1,Основные понятия Теории Вероятности
- •2, Сумма событий. Теорема сложения вероятностей
- •4 Формула полной вероятности.
- •3. Произведение событий
- •5 Формула Бернулли.
- •6. Лаплас .Пуассон
- •7. Дискретной случайной величиной
- •8. Числовые характеристики дискретных случайных величин.
- •16 Точечные оценки параметров распределения
- •9.Непрерывные функции распределения
- •10 Числовые характеристики непрерывных случайных величин.
- •17 Интервальные оценки параметров распределения при известном
- •11, Законы распределения
- •13. Двумерные случайные величины
- •12 Нормальный закон распределения.
- •15 Основные понятия мат статистики
- •18 Интервальные оценки параметров распределения при неизвестнов
- •20. Элементы корреляционного анализа
- •19 Статистическая проверка гипотез
- •25.Симплекс метод
- •1 Этап. Построение первоначального базисного плана.
- •21.Линейная регрессия
- •22.Примеры производственных задач лесного комплекса, приводящие к задачам линейного программирования
- •26. М –задача. Свойства решений м- задачи
- •23.Постановка задачи линейного программирования
- •28. Поток событий. Основные понятия и характеристики
15 Основные понятия мат статистики
Пусть наблюдается (при неизменных условиях) определенный признак некоторой совокупности однородных объектов. Такая совокупность называется генеральной. Совокупность n объектов, отобранных (случайным образом) из генеральной совокупности, называется выборкой (репрезентативной) объема n.
Операция
расположения значений СВ
 (признака) по неубыванию называетсяранжированием
статистических
данных. Упорядоченная таким образом
по неубыванию последовательность
выборочных значений СВ
(признака) по неубыванию называетсяранжированием
статистических
данных. Упорядоченная таким образом
по неубыванию последовательность
выборочных значений СВ
 :
: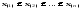 ,
где
,
где ,
,
 ,
называется вариационным
ряд Размахом выборки W
называется разность между максимальным
и минимальным значениями элементов
выборки:
,
называется вариационным
ряд Размахом выборки W
называется разность между максимальным
и минимальным значениями элементов
выборки:
 .В
случае, когда число значений признака
(СВ
.В
случае, когда число значений признака
(СВ )
велико или признак является непрерывным
(т.е. когда СВ
)
велико или признак является непрерывным
(т.е. когда СВ может принимать любое значение в
некотором интервале), составляютинтервальный
статистический ряд
может принимать любое значение в
некотором интервале), составляютинтервальный
статистический ряд
Эмпирической
функцией распределения
называется функция
 ,
определяющая для каждого значения
,
определяющая для каждого значения частость события
частость события :
: ,
,
где
 — объем выборки,
— объем выборки,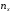 —
число выборочных значений
—
число выборочных значений ,
меньших
,
меньших (
( ).
).
Полигоном
частот
называют ломаную, отрезки которой
соединяют точки с координатами
 ,
, ,…,
,…, ;
полигоном относительных частот —
ломаную, соединяющую точки
;
полигоном относительных частот —
ломаную, соединяющую точки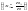

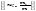 .Гистограммой
частот (относительных частот) называют
ступенчатую фигуру, состоящую из
прямоугольников, основаниями которых
служат частичные интервалы длины
.Гистограммой
частот (относительных частот) называют
ступенчатую фигуру, состоящую из
прямоугольников, основаниями которых
служат частичные интервалы длины
 ,
а высоты равны отношению
,
а высоты равны отношению плотность частоты (
плотность частоты ( —
плотность относительной частоты).
Площадь гистограммы частот равна объему
выборки, а площадь гистограммы
относительных частот равна единице.
—
плотность относительной частоты).
Площадь гистограммы частот равна объему
выборки, а площадь гистограммы
относительных частот равна единице.
.
18 Интервальные оценки параметров распределения при неизвестнов
При
неизвестной дисперсии генеральной
совокупности используется формула
 ,
(6)где
,
(6)где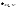 определяется с помощью таблицы значений
распределения Стьюдента (приложение
2) по данному числу степеней свободы
определяется с помощью таблицы значений
распределения Стьюдента (приложение
2) по данному числу степеней свободы и уровню значимости
и уровню значимости .S
− исправленное выборочное среднее
квадратическое отклонение. Отметим,
что при объеме выборки
.S
− исправленное выборочное среднее
квадратическое отклонение. Отметим,
что при объеме выборки
 вместо распределения Стьюдента часто
пользуются нормальным распределением.
вместо распределения Стьюдента часто
пользуются нормальным распределением.
Эмпирическая
функция распределения выборки
 являетсянесмещенной
состоятельной оценкой теоретической
функции распределения
являетсянесмещенной
состоятельной оценкой теоретической
функции распределения
 .
.
Точечные
оценки неизвестного параметра
 хороши в качестве первоначальных
результатов обработки наблюдений.
Недостатком является то, что неизвестно
с какой точностью они дают оцениваемый
параметр.
хороши в качестве первоначальных
результатов обработки наблюдений.
Недостатком является то, что неизвестно
с какой точностью они дают оцениваемый
параметр.
Оценка неизвестного параметра называется интервальной, если она определяется двумя числами — концами интервала, покрывающего оцениваемый параметр.
20. Элементы корреляционного анализа
Корреляционный
анализ исследует взаимосвязь случайных
величин (СВ) на основе экспериментальных
данных. Предположим, что результаты
эксперимента описываются двумя СВ
 и
и .
Они могут быть: 1) независимы; 2) связаны
функциональной зависимостью; 3) связаны
статистической зависимостью.
.
Они могут быть: 1) независимы; 2) связаны
функциональной зависимостью; 3) связаны
статистической зависимостью.
СВ связаны функциональной зависимостью, если одна из них является функцией другой.
Статистической называется зависимость, при которой изменение одной величины влечет изменение распределения другой. Статистическая зависимость возникает из-за того, что на результат эксперимента влияют какие-то неучтенные случайные факторы.
Для
определения статистической зависимости
данные наблюдений СВ
 иY
- двумерной СВ (X,Y),
записывают в виде корреляционной
таблицы
иY
- двумерной СВ (X,Y),
записывают в виде корреляционной
таблицы
В
случае, когда число наблюдаемых
значений СВ
 иY
велико
или СВ являются непрерывными ( т.е.
могут принимать любое значение из
соответствующих интервалов), аналогично
интервальному статистическому ряду
(лаб. раб. №3) составляется интервальная
корреляционная таблица.
иY
велико
или СВ являются непрерывными ( т.е.
могут принимать любое значение из
соответствующих интервалов), аналогично
интервальному статистическому ряду
(лаб. раб. №3) составляется интервальная
корреляционная таблица.
Условным
средним
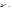 называют среднее арифметическое
значений СВ Y,
соответствующих
значению
называют среднее арифметическое
значений СВ Y,
соответствующих
значению
 .
Например,
.
Например,
 .
.
Корреляционной
зависимостью
Y
от
 называют зависимость условной средней
называют зависимость условной средней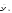 от
x:
от
x:
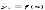
Уравнение
(1) называют
эмпирическим
уравнением
регрессии
Y
на
X;
функцию

 называют
эмпирической
регрессией Y
на
X,
а
ее график - линией регрессии Y
на
X
.
называют
эмпирической
регрессией Y
на
X,
а
ее график - линией регрессии Y
на
X
.
Аналогично
определяются условная средняя
 и корреляционная зависимость
и корреляционная зависимость отY:
отY:

Предварительное
представление о характере зависимости
между
 и
и можно получить, если элементы выборки
можно получить, если элементы выборки ,
, ,
отметить в виде точек на плоскости в
выбранной системе координат. Эта
точечная диаграмма называетсякорреляционным
полем.
,
отметить в виде точек на плоскости в
выбранной системе координат. Эта
точечная диаграмма называетсякорреляционным
полем.
