
- •4. Определенный интеграл с переменным верхним пределом:
- •6. Интегрирование по частям:
- •7. Вычисление площади в декартовой системе координат:
- •12. Несобственные интегралы второго рода:
- •9. Вычисление объема тела вращения:
- •10. Работа переменной силы:
- •11. Несобственные интеграла с бесконечными пределами интегрирования:
- •21. Метод вариации произвольных постоянных:
- •33. Достаточные признаки сравнения:
- •39. Ряды Маклорена для некоторых функций:
- •40. Приложения степенных рядов:
- •53. Нормальное распределение
Если интегральная сумма Sn имеет предел при n-∞(λ-0), который не зависит ни от способа разбиения отрезка на частичные отрезки, ни от выбора точек в них, то он называется определенным интегралом от функции у=f(х) на отрезке [а,в].
Достаточное
условие:
если функция у=f(х)
непрерывна на [а,в], то
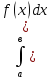 существует.
существует.
Необходимое условие: ограниченность функции на отрезке, но есть функции которые ограничены на отрезке но интегрируемы на нем.
2. Свойства определенного интеграла:
1).
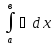 =⍺(b-a)
(⍺-некоторое
число)
=⍺(b-a)
(⍺-некоторое
число)
2).
Пусть f(х)
интегрируема на [а,в] тогда функция ⍺
f(х)
также интегрируема на [а,в] причем
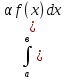 =
=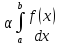
3).
Если f(х),
g(x)
функции интегрируемые на [а,в] то
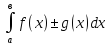 =
=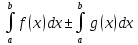
4). Пусть f(х) интегрируема на [а,в], тогда она интегрируема на любом отрезке содержащемся в [а,в], если f(х) интегрируема на [а,с],[с,в], то она интегрируема и на [а,в], причем
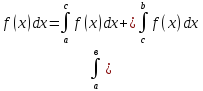
5).
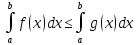 (a˂b)
6).
Пусть m-наименьшее,
М-наибольшее значение функции на отрезке
m≤
f(х)≤М
m(b-a)
(a˂b)
6).
Пусть m-наименьшее,
М-наибольшее значение функции на отрезке
m≤
f(х)≤М
m(b-a)
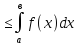 ≤M(b-a)
(a˂b)
≤M(b-a)
(a˂b)
7).
Пусть (а˂в), если f(х)≥0,
х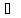 [а,в],
то
[а,в],
то
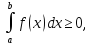 если f(x)≤0
если f(x)≤0
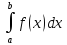 ≤0.
≤0.
8).
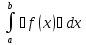 (a˂b) ≥
(a˂b) ≥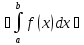
3. Теорема о среднем: -пусть функция f(х) непрерывна на отрезке [a,b] , тогда на этом отрезке существует такая точка С, что
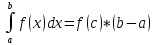
Замечание: величину f(c) равную
f(C)=1/(b-a)*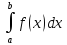
называют средним значением функции f(x) на [a,b].
4. Определенный интеграл с переменным верхним пределом:
Пусть
f(x)
непрерывна на [a,b]
, тогда она интегрируема на любом отрезке
[a,x],
где xϵ
[a,b].
Рассмотрим Ф(х)=
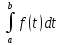 ,
называемую определенным интегралом с
переменным верхним пределом.
,
называемую определенным интегралом с
переменным верхним пределом.
Теорема Барроу: производная определенного интеграла от непрерывной функции по переменному верхнему пределу равна подынтегральной функции вычисленной на верхнем пределе:
(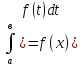
5. Теорема:
если функция f(x)
непрерывна на [a,b],
F(x)-первообразная
для f(x)
на [a,b],
то интеграл
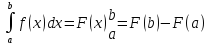 – Формула Ньютона-Лейбница (основная
формула интегрального исчисления).
– Формула Ньютона-Лейбница (основная
формула интегрального исчисления).
6. Интегрирование по частям:
Теорема:
пусть функция u(x),
v(x)
и их производные u,(x),
v,(x),
непрерывны на [a,b],
тогда справедлива формула
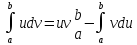 .
.
Метод замены переменных в определенном интеграле:
Теорема: пусть функция f(x) непрерывна на [a,b], а функция x=ϕ(t) непрерывно-дифференцируема на [α,β], причем ϕ(α)=а, ϕ(β)=b и функция a≤ϕ(t)≤b, тогда имеет место формула:
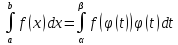
Интегрирование
четных и нечетных функций: пусть
функция f(x)
непрерывна
на [a,b],
тогда вычисление интеграла
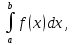 можно упростить учитывая свойства
четности и нечетности функцииf(x).
Имеет место формула:
можно упростить учитывая свойства
четности и нечетности функцииf(x).
Имеет место формула:

7. Вычисление площади в декартовой системе координат:
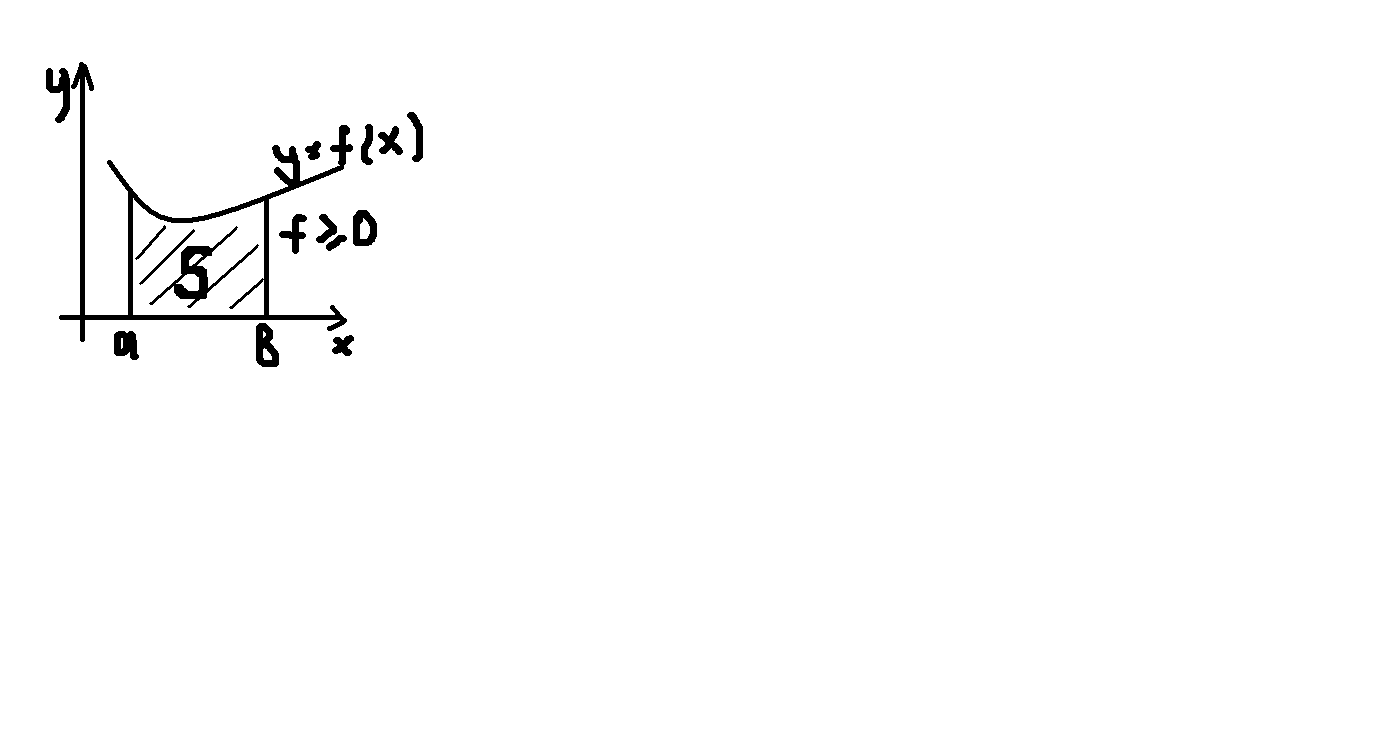
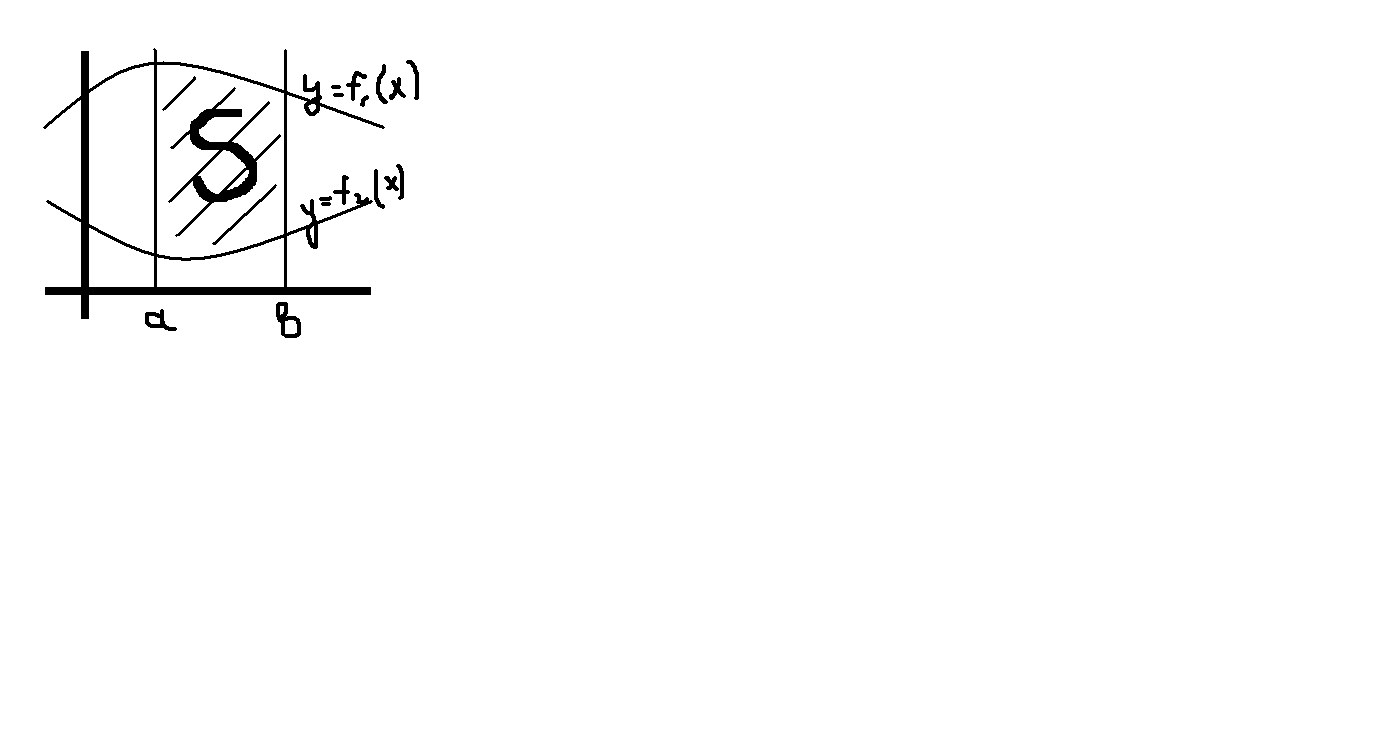
f2(x)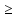 f1(x)
xϵ[a,b]
f1(x)
xϵ[a,b]
S=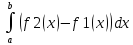

f2≥f1
S=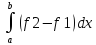
Параметрическое
задание:
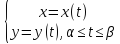
x(α)=a,
x(β)=b
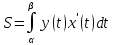
В
полярных координатах:
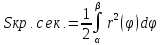
12. Несобственные интегралы второго рода:
Пусть
f(x)
непрерывна на промежутке [a,b)
и неограниченна при x→b
(f(x)→∞
при x→b)
в этом случае несобственный интеграл
2-го рода принимают следующим образом:
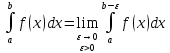 .
.
Если предел существует, говорят, что интеграл сходится, не существует или бесконечен – расходится.
Теорема
(сравнения): пусть
на промежутке [a,b)
функции f(x),
ϕ(x)
непрерывны и f(x)→∞,
ϕ(x)→∞
при x→b
при этом 0≤f(x)≤ϕ(x)
тогда из сходимости интеграла: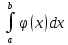 следует сходимость
следует сходимость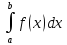 ,
а из расходимости
,
а из расходимости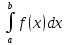 следует расходимость
следует расходимость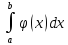 .
.
Теорема
(предельный признак сравнения):
пусть на промежутке [a,b)
функции f(x),
ϕ(x)
непрерывны и f(x)→∞,
ϕ(x)→∞
при x→b
при этом 0≤f(x)≤ϕ(x)
если существует предел:
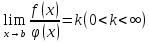 ,
то интегралы
,
то интегралы
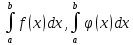 либо оба сходятся либо оба расходятся.
либо оба сходятся либо оба расходятся.
9. Вычисление объема тела вращения:
Пусть
вокруг оси Ох вращения криволинейная
трапеция, ограниченная кривой у=f(x)
,
прямыми
х=0, х=в и Ох и пусть f(x)
непрерывная на [a,b]
функции (f˃0),
получим тело вращения V
которого вычисляется по формуле:
(Vox=π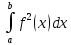 )*
)*
Разобьем
отрезок [a,b]
на n
частей в каждой части произвольно
выберем точку Ci
ϵ
[Xi-1,X1],
проведем, через точки Xi
плоскости ˔
Ох получим слоев тела вращения, каждый
слой замещением цилиндра высотой
ΔXi=Xi-Xi-1
и основанием является круг радиуса
f(Ci).
Сумарный объем ступенчатого тела равен
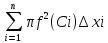 ,
переходя к пределу прі n
,
переходя к пределу прі n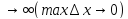 получім
формулу (*).
получім
формулу (*).
10. Работа переменной силы:
Пусть
материальная точка переменной под
действием силы F
направленной вдоль оси Ох и имеющей
переменную величину зависящей от х
F=F(x),
покажем, что работа совершаемая силой
F
по перемещению точки вдоль оси Ох из
х=а в х=в вычисляется по формуле: A=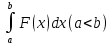
(F , непрерывна на [a,b])
