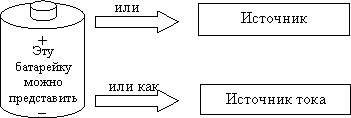
1 Реальные и идеальные источники эл. энергии. Схемы замещения. Любой источник электрической энергии преобразует другие виды энергии (механическую, световую, химическую и др.) в электрическую. Ток в источнике электрической энергии направлен от отрицательного вывода к положительному за счет сторонних сил, обусловленных видом энергии, которую источник преобразует в электрическую. Реальный источник электрической энергии при анализе электрических цепей можно представить либо в виде источника напряжения, либо в виде источника тока. Ниже это показано на примере обыкновенной батарейки.

Рис. 14. Представление реального источника электрической энергии либо в виде источника напряжения, либо в виде источника тока

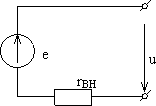
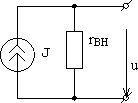
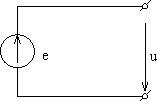
Способы представления реального источника электрической энергии отличаются друг от друга схемами замещения (расчетными схемами). На рис. 15 реальный источник представлен (замещен) схемой источника напряжения, а на рис. 16 реальный источник представлен (замещен) схемой источника тока.

	Рис. 15. Схема замещения реального источника  напряжения		Рис. 16. Схема замещения реального источника  тока

Как видно из схем на рис. 15 и 16, каждая из схем имеет идеальный источник (напряжения или тока) и собственное внутреннее сопротивление r_ВН. Если внутреннее сопротивление источника напряжения равно нулю (r_ВН=0), то получается идеальный источник напряжения (источник ЭДС). Если внутреннее сопротивление источника тока бесконечно велико (r_ВН=), то получается идеальный источник тока (источник задающего тока). Схемы идеальных источника напряжения и идеального источника тока показаны на рис. 17 и 18. Отметим особо, что обозначать идеальный источник тока будем буквой J.

 

 

Рис. 17. Схема замещения идеального источника  напряжения (источника ЭДС)

Рис. 18. Схема замещения идеального источника  тока

2. Цепи переменного тока. Однофазный переменный ток. Основные хар-ки, частоты фазы, начальная фаза. ПЕРЕМЕННЫЙ ОДНОФАЗНЫЙ ТОК. Ток, изменяющийся во времени по значению и направлению, называется переменным. В практике применяют периодически изменяющийся по синусоидальному закону переменный ток (рис. 1).Синусоидальные величины характеризуются следующими основными параметрами: периодом, частотой, амплитудой, начальной фазой или сдвигом фаз.

Рис. 1   График синусоидальной величины

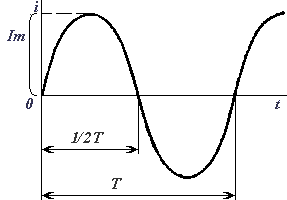
Период (T) - время (с), в течение которого переменная величина совершает полное колебание. Частота - число периодов в секунду. Единица измерения частоты - Герц (сокращенно Гц), 1 Гц равен одному колебанию в секунду. Период и частота связаны зависимостью T = 1 / f. Изменяясь с течением времени, синусоидальная величина (напряжение, ток, ЭДС) принимает различные значения. Значение величины в данный момент времени называют мгновенным. Амплитуда - наибольшее значение синусоидальной величины. Амплитуды тока, напряжения и ЭДС обозначают прописными буквами с индексом: I_m, U_m, E_m, а их мгновенные значения - строчными буквами i, u, e. Мгновенное значение синусоидальной величины, например тока, определяют по формуле i = I_msin(ωt + ψ), где ωt + ψ — фаза-угол, определяющий значение синусоидальной величины в данный момент времени; ψ - начальная фаза, т. е. угол, определяющий значение величины в начальный момент времени. Синусоидальные величины, имеющие одинаковую частоту, но разные начальные фазы, называются сдвинутыми по фазе.

3 На рис. 2 приведены графики синусоидальных величин (тока, напряжения), сдвинутых по фазе. Когда же начальные фазы двух величин равны ψ_i = ψ_u, то разница ψ_i − ψ_u = 0 и, значит, сдвига фаз нет φ = 0 (рис. 3). Эффективность механического и теплового действия переменного тока оценивается действующим его значением. Действующее значение переменного тока равно такому значению постоянного тока, который за время, равное одному периоду переменного тока, выделит в том же сопротивлении такое же количество тепла, что и переменный ток. Действующее значение обозначают прописными буквами без индекса: I, U, E. Рис. 2   Графики синусоидальных тока и напряжения, сдвинутых по фазе. Рис. 3   Графики синусоидальных тока и напряжения, совпадающих по фазе

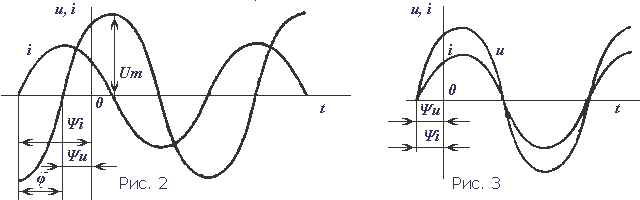
Для синусоидальных величин действующие и амплитудные значения связаны соотношениями:

I=I_M/√2;   U=U_M/√2;   E=E_M√2. Действующие значения тока и напряжения измеряют амперметрами и вольтметрами переменного тока, а среднее значение мощности - ваттметрами.

4.Действующим (эффективным) значением силы переменного тока называют величину постоянного тока, действие которого произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток за время одного периода. В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение силы переменного тока. Иначе говоря, действующее значение тока можно определить по формуле:

.

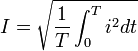Для гармонических колебаний тока

 

5Формула индуктивного сопротивления:

где L — индуктивность.

Формула емкостного сопротивления:

где С — емкость.

Предлагаем рассмотреть цепь переменного тока, в которую включено одно активное сопротивление, и нарисовать ее в тетрадях. После проверки рисунка рассказываю, что в электрической цепи (рис. 1, а) под действием переменного напряжения протекает переменный ток, изменение которого зависит от изменения напряжения. Если напряжение увеличивается, ток в цепи возрастает, а при напряжении, равном нулю, ток в цепи отсутствует. Изменение направления его также будет совпадать с изменением направления напряжения

(рис. 1, в).

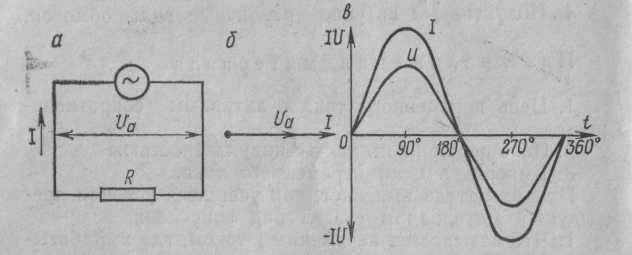
Рис 1. Цепь переменного тока с активным сопротивлением: а – схема; б – векторная диаграмма; в – волновая диаграмма

Графически изображаю на доске синусоиды тока и напряжения, которые совпадают по фазе, объясняя, что хотя по синусоиде можно определить период и частоту колебаний, а также максимальное и действующее значения, тем не менее построить синусоиду довольно сложно. Более простым способом изображения величин тока и напряжения является векторный. Для этого вектора напряжения (в масштабе) следует отложить вправо из произвольно выбранной точки. Вектор тока преподаватель предлагает учащимся отложить самостоятельно, напомнив, что напряжение и ток совпадают по фазе. После построения векторной диаграммы (рис. 1, б) следует показать, что угол между векторами напряжения и тока равен нулю, т. е. ? = 0. Сила тока в такой цепи будет определяться по закону Ома: Вопрос 2. Цепь переменного тока с индуктивным сопротивлением Рассмотрим электрическую цепь переменного тока (рис. 2, а), в которую включено индуктивное сопротивление. Таким сопротивлением является катушка с небольшим количеством витков провода большого сечения, в которой активное сопротивление принято считать равным 0.

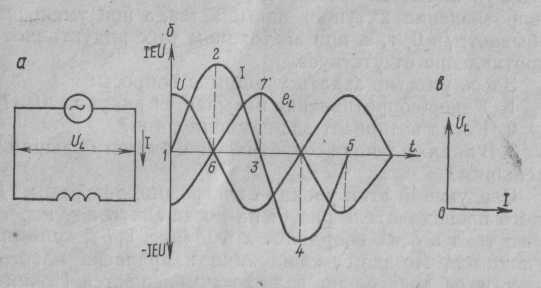
Рис. 2. Цепь переменного тока с индуктивным сопротивлением

Вокруг витков катушки при прохождении тока и будет создаваться переменное магнитное поле, индуктирующее в витках эдс самоиндукции. Согласно правилу Ленца, эде индукции всегда противодействует причине, вызывающей ее. А так как эде самоиндукции вызвана изменениями пе-ременного тока, то она и препятствует его прохождению. Сопротивление, вызываемое эде самоиндукции, называется индуктивным и обозначается буквой x_L. Индуктивное со-противление катушки зависит от скорости изменения то-ка в катушке и ее индуктивности L: где Х_L– индуктивное сопротивление, Ом; – угловая частота переменного тока, рад/с; L–индуктивность ка-тушки, Г.

Угловая частота == ,

следовательно, .

Емкостное сопротивление в цепи переменного тока. Перед началом объяснения следует напомнить, что имеется ряд случаев, когда в электрических цепях, кроме активного и индуктивного сопротивлений, имеется и емкостное сопротивление. Прибор, предназначенный для накопления электрических зарядов, называется конденсатором. Простейший конденсатор – это два проводка, разделенных слоем изоляции. Поэтому многожильные провода, кабели, обмотки электродвигателей и т. д. имеют емкостное сопротивление. Объяснение сопровождается показом конденсатора различных типов и емкостных сопротивлений с подключением их в электрическую цепь. Предлагаю рассмотреть случай, когда в электрической цепи преобладает одно емкостное сопротивление, а активным и индуктивным можно пренебречь из-за их малых значений (рис. 6, а). Если конденсатор включить в цепь постоянного тока, то ток по цепи проходить не будет, так как между пластинами конденсатора находится диэлектрик. Если же емкостное сопротивление подключить к цепи переменного тока, то по цепи будет проходить ток /, вызванный перезарядкой конденсатора. Перезарядка происходит потому, что переменное напряжение меняет свое направление, и, следовательно, если мы подключим амперметр в эту цепь, то он будет показывать ток зарядки и разрядки конденсатора. Через конденсатор ток и в этом случае не проходит. Сила тока, проходящего в цепи с емкостным сопротивлением, зависит от емкостного сопротивления конденсатора Хс и определяется по закону Ома 

где U – напряжение источника эдс, В; Хс – емкостное сопротивление, Ом; / – сила тока, А.

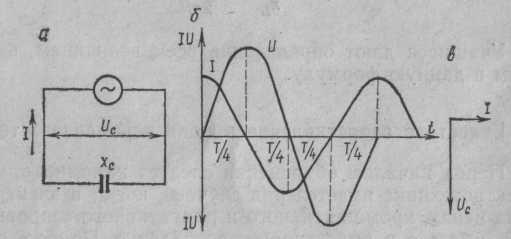
Рис. 3. Цепь переменного тока с емкостным сопротивлением

Емкостное сопротивление в свою очередь определяется по формуле 

где С – емкостное сопротивление конденсатора, Ф. Предлагаю учащимся построить векторную диаграмму тока и напряжения в цепи с емкостным сопротивлением. Напоминаю, что при изучении процессов в электрической цепи с емкостным сопротивлением было установлено, что ток опережает напряжение на угол ф = 90°. Этот сдвиг фаз тока и напряжения следует показать на волновой диаграмме. Графически изображаю на доске синусоиду напряжения (рис. 3, б) и дает задание учащимся самостоятельно нанести на чертеж синусоиду тока, опережающую напряжение на угол 90°