
Метрология В-5 .doc пятый вариант... может помо
...doc46. При определении концентрации кофеина в кофе молотом в зернах хроматографическим методом были получены следующие результаты (мг/г):
|
16,20 |
16,39 |
13,75 |
13,71 |
14,08 |
16,06 |
16,18 |
16,14 |
15,90 |
15,86 |
14,99 |
17,97 |
|
16,45 |
16,41 |
16,52 |
16,48 |
14,56 |
15,84 |
16,06 |
16,00 |
13,87 |
13,99. |
|
|
Погрешность жидкостного хроматографа составляет 9,8 %. Погрешность пробоподготовки состоит из погрешности чистоты применяемого реактива – 0,5 %, погрешности взвешивания навески – 0,1 г на равноплечих весах 2-го кл. точности (погрешность ±0,15 мг) и погрешности измерения объемов – 4,5 % . Рассчитанное значение погрешности построения градуировочного графика составляет 10 %. Провести обработку и оценить точность результата.
Решение:
Правила обработки результатов прямых измерений с многократными наблюдениями регламентирует ГОСТ 8.207-76.
Обработка результатов наблюдений проводится в следующей последовательности.
1. Исключаем известные систематические погрешности из результатов наблюдений (введение поправки).
2. Исключить из результатов наблюдений результаты с грубыми погрешностями.
Воспользуемся
критерием «трех сигм»,
![]() ,
в нашем случае
,
в нашем случае
![]() .
.
![]() – промах, если
выполняется следующее условие
– промах, если
выполняется следующее условие
![]() .
.
Величины
![]() и
и
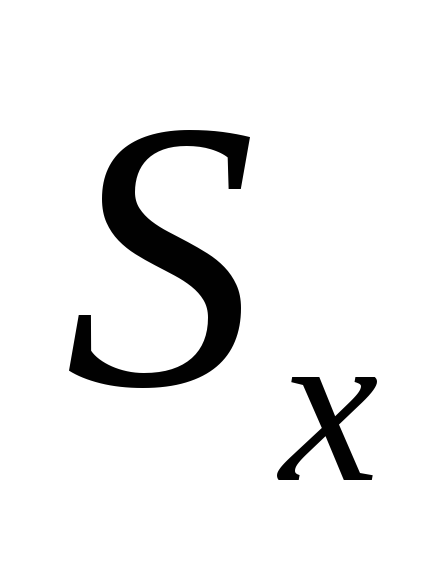 вычисляют без учета экстремальных
значений
вычисляют без учета экстремальных
значений
![]() .
.
Проверим на наличие
промаха
![]() .
.
![]()
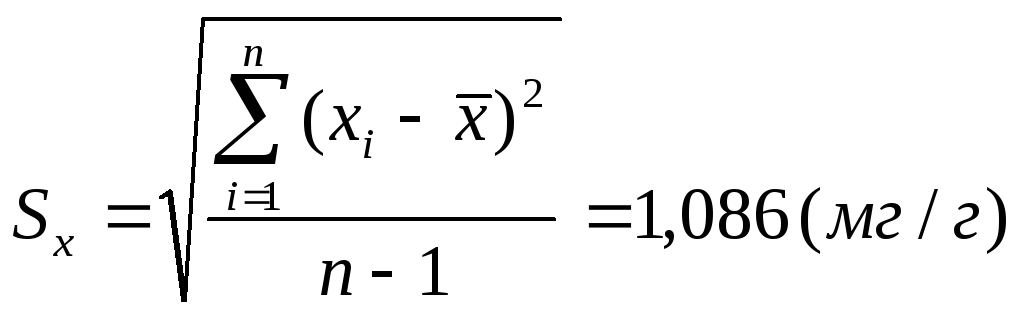
![]()
![]() – не является
промахом.
– не является
промахом.
Проверим на наличие
промаха
![]() .
.
![]()
![]()
![]()
![]() – не является
промахом.
– не является
промахом.
3.
Вычислим среднее арифметическое
исправленных (после введения поправки)
результатов наблюдений
![]() ,
принимаемое за результат измерения,
,
принимаемое за результат измерения,
![]()
4.
Вычислим оценку среднего квадратического
отклонения результатов наблюдений
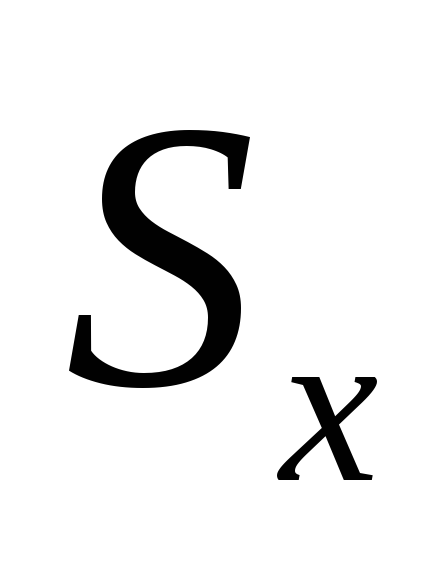
![]()
5.
Вычислим оценку среднего квадратического
отклонения результата измерения
(среднего арифметического)
![]()
![]()
6.
Определим доверительные границы
случайной погрешности результата
измерения
![]() при заданной доверительной вероятности
при заданной доверительной вероятности
![]() и
и
![]() :
:
При
![]() доверительные границы определяют по
формуле:
доверительные границы определяют по
формуле:
![]()
Воспользуемся
формулой нахождения истинного значения
в доверительном интервале
![]() .
Отсюда значение
.
Отсюда значение
![]() ,
т.е.
,
т.е.
![]() По таблицам значений функции нормированного
нормального распределения находим
значение аргумента
По таблицам значений функции нормированного
нормального распределения находим
значение аргумента
![]() ,
при котором функция примет значение,
равное
,
при котором функция примет значение,
равное
![]() .
Доверительные границы равны:
.
Доверительные границы равны:
![]()
7. Вычислим границы суммарной неисключенной систематической погрешности результата измерений, которая образуется из неисключенных систематических погрешностей метода, средств измерений, погрешностей поправок и др.
![]()
где
![]() – коэффициент, определяемый принятой
доверительной вероятностью и
количеством неисключенных составляющих;
– коэффициент, определяемый принятой
доверительной вероятностью и
количеством неисключенных составляющих;
![]() – количество
неисключенных составляющих;
– количество
неисключенных составляющих;
![]() – границы
– границы
![]() -й
неисключенной составляющей
систематической погрешности. При
доверительной вероятности
-й
неисключенной составляющей
систематической погрешности. При
доверительной вероятности
![]() ,
если число суммируемых неисключенных
систематических погрешностей более
четырех
,
если число суммируемых неисключенных
систематических погрешностей более
четырех
![]() .
.
![]()
![]()
8. Вычислим доверительные границы погрешности результата измерения.
![]()
Поскольку
![]() ,
то случайной погрешностью можно
пренебречь и принять границы погрешности
результата
,
то случайной погрешностью можно
пренебречь и принять границы погрешности
результата
![]() равными
равными
![]() .
.
![]()
9. Представим результат измерений.
![]() ,
при
,
при
![]()
![]() ,
при
,
при
![]()
Литература
1. Н.И. Заяц Метрология. Программа, методические указания и контрольные задания для студентов-заочников специальности «Физико-химические методы и приборы контроля качества продукции». – Мн.: БГТУ, 2005
2. Ламоткин, С.А. Основы стандартизации, сертификации, метрологии: учеб. пособие для студентов экономических специальностей / С.А. Ламоткин, З.Е. Егорова, Н.И. Заяц. – Мн.: БГТУ, 2005, – 372.
.
