

ТЕМА VIІІ. ПЕРЕРІЗ КРИВИХ ПОВЕРХОНЬ ПЛОЩИНОЮ І ПРЯМОЮ ЛІНІЄЮ.
VIІІ.1 Переріз кривих поверхонь площиною.
При перетині поверхні площиною одержуємо плоску фігуру, яка називається перерізом. Визначення проекцій ліній переріза починають з будови опорних точок – найвищих , найнижчих, лівих, правих, точок злому й переходу від видимої до невидимої частини. Розглянемо приклад переріза сфери фронтально-проеціюючою площиною. Переріз сфери будь якою площиною є круг. Фронтальна проекція круга (Рис.70) збігається із слідом – проекцією площини (2). Горизонтальна проекція – еліпс. Побудову еліпса починаємо з опорних точок. Точки А і В належать великої осі еліпса у яку проеціюється круг. Знайдемо малу вісь еліпса. Ділимо А2В2 навпіл і отримуємо точку N, яка належить паралелі, радіус якої дорівнюється відстані від осі обертання до фронтального меридіану сфери. Знайдемо горизонтальну проекцію точок N1 і N'1. Визначаємо точки переходу від видимої до невидимої частини, які належать екватору сфери точки M1 M'1. додаткові точки знаходимо за допомогою паралелів, проведених через точки взяті на сліді – проекції проеціюючої площини.
Рис.70
VIІІ.2 Перерізи конічних поверхонь.
На Рис.71 показано можливі випадки перерізів прямого кругового конуса січною площиною. При цьому можуть бути такі фігури перерізу:
—коло – січна площина перпендикулярна до осі обертання конуса (Рис.71а);
—прямі лінії (твірні) – січна площина проходить через вершину (Рис.71б);
—еліпс – січна площина перетинає всі твірні бічної поверхні (Рис.71в);
—парабола – січна площина паралельна одній з твірним бічної поверхні (Рис.71г)
—гіпербола – січна площина паралельна двом твірним бічної поверхні (Рис.71д).
а) |
б) |
1

в) |
г) |
д) Рис.71
Розглянемо приклад побудови переріза прямого кругового конуса фронтальнопроеціюючою площиною (Рис.72). Січна площина перетинає всі твірні бічної поверхні.
Побудуємо проекцію фігури перерізу на П1 і її дійсний розмір. Площина 2 фронтально-проеціююча і на П2 вона проеціюється прямою (слід-проекція площини ). Фронтальна проекція еліпса збігається зі слідом – проекцієй 2. Для побудови еліпса на П1 виділяємо точки на твірних бічної поверхні конуса А2, В2 і проеціюємо їх на П1 – велика вісь еліпса. Ділимо А2В2 навпіл і отримуємо точку С. Через т. С(С2) проводимо пряму паралельну основі конуса. Проекція на П1 цієї прямої є коло. Радіус кола дорівнюється відстані до осі обертання конуса. На П1 проводимо коло цього радіуса і на нього проеціюємо т. С(С1С'1). С1С'1 – мала вісь еліпса (Рис.72).Точку С(С')можна побудувати іншим способом. Через вершину конуса S(S2) і точку С(С2) проводимо пряму до перетину її з основою. Знаходимо горизонтальну проекцію цієї прямої і на неї проеціюємо т. С, С'. Дійсний розмір еліпса визначаємо за допомогою способу заміни площин проекцій.
На Рис.73 приведено приклад побудови еліпса при перерізі конуса площиною (h ∩ f) загального положення. Спочатку визначаємо особливі точки – точки, які належать крайнім твірним бічної поверхні, а також вищу й нищу точки.
Для побудови цих точок застосовуємо допоміжні площини (січні), як правило, проеціюючи, або площини рівня. Крайні точки А і В знайдені за допомогою площини (1) – площина фронтального рівня. Ця площина перетинає конус по трикутнику, а площину (h ∩ f) по фроталі. Перетин трикутника із фронталлю дає точки А і В. Точки А (А2) і В(В2) ділять січну на видиму й невидиму. Вищу і нищу точки визначаємо за допомогою горизонтально-проеціюючої площині (1). Вища і нища точки належать лінії найвищого нахилу площини (h ∩ f). Січну площину (1) П1 проводимо перпендикулярно h1 площини (h ∩ f) і через вершину S(S1) конуса. Площина (1) перетинає конус по трикутнику 52S262, а площину ( h ∩ f) по прямій 1 – 2. Перетин трикутника 52S262 і прямої 12 - 22 дає вищу і нищу точки D і C. Додаткові точки знаходимо за допомогою січних площин горизонтального рівня.
2
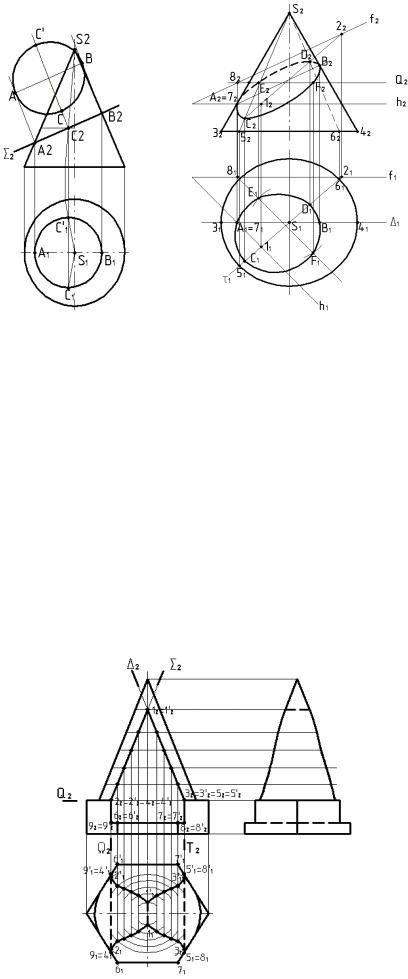
Рис.72 Рис.73
Розглянемо приклад побудови зображень геометричних тіл з одинарним проникненням.
Геометричне тіло з одинарним проникненням (Рис.74) складається з двох геометричних фігур – конуса (верхня частина) і призми (нижня частина). В цьому геометричному тілі виготовлено складний наскрізний отвір, обмежений різними площинами (площини рівня, проеціюючи площини). При зображенні проекцій цього тіла вся складність полягає в побудові ліній перетину цих площин з поданими фігурами, які треба будувати по точкам. Так, площини ∆2 і 2 перетинають конус по параболам, які обмежені точками зверху 12 (видима), 12 (невидима), на основі 22(22 ) і 32(32 ). Для того, щоб знайти горизонтальні проекції точок 11(11), 21(21), 31(31 ), та допоміжних точок проводимо на фронтальній проекції через ці точки лінії перпендикулярні вісі обертання конуса. які на П1 проеціюються колами радіус яких дорівнюється відстані від осі
обертання до бічної твірної. Площини Q2, T2 , 2 будуть перетинати шестикутну призму по лініях, обмежених точками 4(4), 9(9 ), 6(6 ), 7(7 ), 8(8 ), 5(5), які належать граням і ребрам фігури. Знаючи положення всіх точок на горизонтальній і фронтальній проекціях будуємо профільну проекцію.
Рис.74
3

VІІІ.3 Перетин прямої й поверхні.
Пряма перетинає поверхню у двох її точках. Для того, щоб знайти точки перетину прямої з поверхнею (призми, піраміди, конуса, циліндра тощо) діють так же як у випадку знаходження точки перетину прямої й площини.
1) через пряму проводимо допоміжну січну площину і знаходимо лінію перерізу із січною площиною. Перетин лінії перерізу поверхні з однойменною проекцією прямої, дає шукані точки перетину прямої й поверхні.
Якщо пряма, або поверхня, які перетинаються, займають у просторі часткове положення, то точка їх перетину збігається зі слідом – проекцій проеціюючої прямої, або поверхні (Рис.75а, б, в).
а) |
б) |
в) |
|
Рис.75 |
|
Приклад визначення точок перетину прямої l з поверхнею похилої тригранної призми приведений на Рис.76. Через пряму проводимо допоміжну січну площину (фронтально – проеціюючу) (2). Площина (2) перерізає призму по трикутнику 123. Перетин горизонтальної проекції трикутника 123 (112131) із горизонтальною проекцією прямої l(l1) дає точки перетину XY.
Рис.76
Для визначення точок перетину прямої з поверхнею еліптичного циліндра, або похилого конуса через пряму проводимо допоміжну січну площину загального положення. Січна площина перерізає поверхню циліндра по чотирикутнику, якщо вона завдана двома пересічними прямими – для циліндра – одна пряма завдана, а друга, паралельна твірній циліндра, а для конуса – одна пряма завдана, а інша проходить через вершину конуса (Рис.77, 79).
4

Площина основ циліндра та конуса розташовані у площині П1, тобто на П1 вони спроеціювались своїм горизонтальним слідом. Перетин горизонтальних проекцій слідів січної площини, та основи поверхні дає точки, із яких будується чотирикутник, або трикутник перерізу поверхні січною площиною. Перетин однойменних проекцій чотирикутника, або трикутника з прямою дає точки перетину прямою з поверхнею
(Рис.78, 80).
Рис.77 |
Рис.78 |
Рис.79 |
Рис.80 |
ЗАПИТАННЯ ДО ТЕМИ.
1.Якщо пряма чи поверхня, що перетинаються, займають у просторі проеціююче положення, як визначаємо точки їх перетину?
2.Які площини – посередники застосовуються для визначення точок перетину прямої і поверхні?
3.Покажіть графічно, як побудувати точки перетину прямої з конусом та похилим циліндром.
4.Яку назву має фігура перетину поверхні площиною.
5.Перелічити можливі випадки перерізів прямого кругового конуса.
6.З яких точок розпочинають побудову проекцій фігури переріза?
7.При перетині прямого кругового конуса площиною загального положення, як знаходять особливі точки фігури переріза?
8.Які способи використовують для знаходження точок, які належать лінії перерізу поверхні площиною?
5

ЗАДАЧІ ДЛЯ САМОСТІЙНОЇ РОБОТИ |
|
а, б, в – побудувати переріз поверхонь площиною. |
|
2 |
2 |
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
б) |
в) |
||||||
l2
l2
l2
l1 |
l1 |
l1
г) д) е)
г, д, е – побудувати точки перетину прямої і поверхні.
6
ЛІТЕРАТУРА
Базова
1.Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии. М. «Наука»,
1988.
2.Нарисна геометрія. Фольта О.В., Антонович Е.А., Юрковський Б.В. Л. “Світ”, 1994.
3.Бубенников А.В. Начертательная геометрия. – М.: Наука, 1985. – 296 с.
4.Виноградов В.Н. Начертательная геометрия: Учебник. – 2-е изд., пере раб. – М.: Просвещение, 1989. – 239 с.
5.Чекмарев А.А. Начертательная геометрия и черчение: Учеб. пособие для студентов пед. ин-тов. – М.: Просвещение, 1987. – 400 с.
6.Нарисна геометрія: Підручник / В.Є. Михайленко, М.Ф. Євстіфєєв, С.М. Ковальов, О.В. Кащенко; За ред. В.Є. Михайленко. – 2-ге вид., переробл. – К.: Вища школа., 2004. – 303 с.: іл.
Допоміжна
1.Ванін В.В.та ін. Оформлення графічної документації: Навчальний посібник.-К.: Каравела,-2003.-160 с.
2.Посвянский. Краткий курс начертательной геометрии. – М.: Наука, -1979.
3.Посвянский. Сборник задач по начертательной геометрии. – М.: Высшая школа, 1978.- 320 с.
4.Система конструкторської документації. Терміни та визначення основних понять. ДСТУ 3321-96. Держстандарт України. – К. 1996. – 80 с.
5.ЕСКД. Основные положения. М.: Изд-ство стандартов,1984. – 344 с.
6.ЕСКД. Общие правила выполнения чертежей. ГОСТ 2.301-68…2.320-82.
7.Збірник задач з інженерної та комп’ютерної графіки: Навч. посіб. / В.Є. Михайленко, В.М. Найдиш, А.М. Підкоритов, І.А. Скидан; За ред. В.Є. Михайленко. – К.: Вища шк., 2002. – 159 с.: іл.
Інформаційні ресурси
1.Начертательная геометрия. Электронный учебник. Св-во № 2001611308, РОСПАТЕНТ, Москва, 1.10.01 г. [Електронний ресурс]. Режим доступу: http://degispstu.narod.ru/
2.Мультимедийные лекции по начертательной геомтерии / И.Д. Столбова, Е.С. Дударь [Електронний ресурс]. Режим доступу: http://nachertalka.siteeditworld.ru/files
http://nachertalka.siteeditworld.ru/files
3.Библиотека технической литературы. ГОСТы. [Електронний ресурс]. Режим доступу: http://tehlib.com.ua/Gost_1_30.htm
4.Учебник «Начертательная геометрия» / В.А. Лалетин, Е.П. Александрова и др. [Електронний ресурс]. Режим доступу: http://nachertalka.siteeditworld.ru/files
7
