
ТЕМА ХІ. АКСОНОМЕТРИЧНІ ПРОЕКЦІЇ.
Аксонометричними називають зображення, що дістали в результаті проеціювання паралельними променями предмета разом з осями прямокутних координат на одну площину проекцій. Якщо проеціюючі промені перпендикулярні до площини аксонометричних проекцій, то аксонометрію називають прямокутною, коли проеціюючі промені не перпендикулярні до площини аксонометричних проекцій – косокутною. Напрям проеціювання вибирають таким, щоб проеціюючі промені не були паралельними жодній з площин, утворених осями координат. Тому на аксонометричному зображенні предмета видно всі три його головні виміри: висоту, що вимірюється вздовж осі Z, а ширину – вздовж осі Y, довжину – вздовж осі Х. Унаслідок цього аксонометричне зображення предмета виходить наочнішим, ніж зображення його в ортогональних проекціях.
Відрізки осей координат проеціюються на площину аксонометричних проекцій у загальному випадку із спотворенням.
Спотворюються і розміри предметів, що проеціюються. Зміна лінійних розмірів уздовж осей характеризується показниками створення. Показником спотворення називається відношення довжини відрізка на аксонометричній осі до довжини того самого відрізка на відповідній осі прямокутної системи координат у просторі.
Якщо умовно показник створення по осі Х позначити буквою k, по осі Y – буквою m і осі Z – буквою n, то K = Ok Xk / OX, m = OkYk / OY, n = OkZk / OZ.
Показники спотворення можуть бути меншими, більшими, дорівнювати одиниці; їх, величина залежить від взаємного положення осей координат і площини аксонометричних проекцій.
Аксонометричні проекції називаються ізометричними, або ізометрією, якщо показники спотворення по всіх осях однакові, тобто k = m = n.
Якщо показники спотворення однакові тільки по двох осях, тобто k = n m проекції називаються диметричними, або диметрією.
Ізометрія, диметрія можуть бути прямокутними або косокутними.
Для наочного зображення предметів ГОСТ 2. 317 – 69 встановив такі види аксонометричних проекцій: прямокутну ізометричну, прямокутну диметричну, косокутну (фронтальну) ізометричну, косокутну (горизонтальну) ізометричну.
За ГОСТ 2. 317 – 68 ізометричну проекцію пропонують будувати без скорочення по осях X, Y, Z, а диметричну – без скорочення по осях X і Z та із скороченням у два рази по осі Y. Тим самим в ізометрії, які вимірюються вздовж аксонометричних осей збільшуються у 1 / 0,82 = 1,22, а в симетрії у 1 / 0,94 = 1,06 рази. У косокутній (фронтальній) диметричній проекції показники спотворення по осях X і Z дорівнюють 1, по осі Y – 0,5.
ХІ.1 Ізометрична проекція.
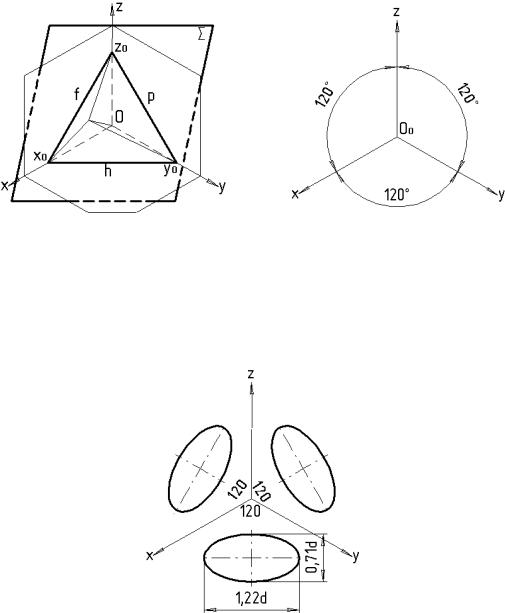
Ізометрія – аксонометрична проекція з коефіцієнтами спотворення, однаковими по всіх трьох осях. Кути між осями дорівнюють 120° (Рис.99а, б).
1
а) |
б) |
Рис.99
Кола, розміщенні у площинах, паралельних площинам проекцій, проеціюються у вигляді однакових еліпсів, великі осі яких розташовані на площині XOY під кутом 90° до осі Z, на площині XOZ – під кутом 90° до осі Y. На площині YOZ – під кутом до осі Х. Великі осі дорівнюють 1,22, а малі – 0,71 діаметра кола (Рис.100).
Рис.100
ХІ.2 Диметрична проекція.
Диметрія – аксонометрична проекція з коефіцієнтами спотворення, однаковими по двох осях. Як правило, диметричну проекцію виконують без спотворення по осях X і Z, із коефіцієнтом спотворення 0,5 по осі Y.
Кола, що лежать у площинах, паралельних площині проекцій, проеціюються на аксонометричну площину проекцій у вигляді еліпсів (Рис.101). Якщо диметричну проекцію виконують без спотворення по осях X і Z, то велика вісь еліпсів дорівнює 1,06 діаметра кола, а мала вісь площин XOY, ZOY – 0,35 діаметра кола. Для площин XOZ мала вісь еліпса дорівнює 0,95 діаметра.
2
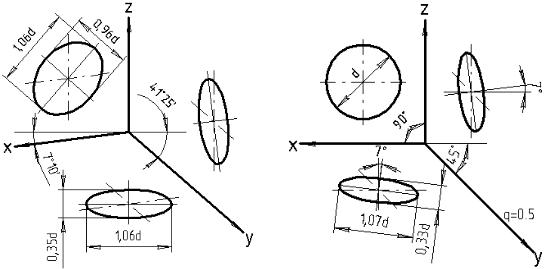
Рис.101 |
Рис.102 |
ХІ.3 Фронтальна диметрична проекція.
Положення диметричних осей при цьому і кути між ними показано на Рис.102, коефіцієнти спотворення по осі У – 0,5, а по осях X і Z – 1.
Кола, що лежать у площинах, паралельних горизонтальній і профільній площинам проекцій проеціюються у еліпси. Велика вісь еліпсів паралельних П1і П3 дорівняє 1,07, мала – 0,33 діаметра кола. Кола, що лежать у площинах, паралельних фронтальній площині проекцій, проеціюються у кола (Рис.102). Фронтальна диметрична проекція, простіша за будовою, ніж прямокутна диметрична, але остання научніше.
ХІ.4 Приклад побудови прямокутної диметрії призми.
Для призми осі координат проводимо так, щоб вони співпадали з головними осями симетрії. При цьому початок координат буде знаходитись в центрі нижньої основи призми, вершини чотирикутника основи на осях x і y (Рис.103).
Будуємо осі координат в прямокутній діметрії. На осі x відкладаємо по обидва боки від точки 00 відрізки 0010 і 0030 рівні відповідно відрізкам 0111 і 0131 на горизонтальній проекції призми. На осі y по обидва боки від точки 00 відкладаємо відрізки 0020 і 0040, рівні відповідно половинам відрізків 0121 і 0141. Сполучая точки 10, 20, 30, 40 отримуємо аксонометричне зображення основи призми. Відкладаючи від початку координати по осі Z відрізок, рівний висоті призми, будуємо її верхню основу. З’єднав точки верхньої і нижньої основи, отримаємо аксонометричне зображення призми. Призму перерізають п’ять площин T(T2), Δ(Δ2), Σ(Σ2), Q(Q2), (2) (площини рівня та фронтально-проеціюючі площини). Точки лінії перетину належать ребрам призми.
3
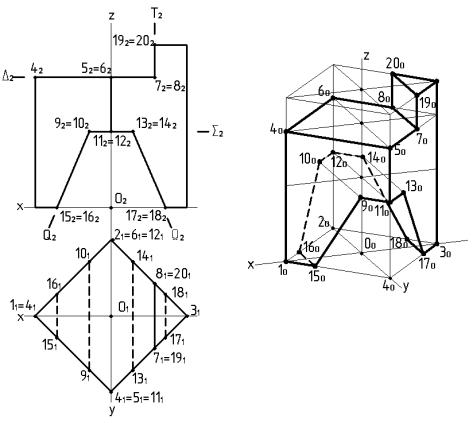
Рис.103
Площина Δ(Δ2) перерізає призму по п’ятикутнику 4, 5, 7, 8, 6. Площина T(T2) перерізає призму по чотирикутнику 7, 8, 20, 19. Площина Σ(Σ2) перерізає призму по шестикутнику 11, 9, 10, 12, 14, 13. Площина Q(Q2) і (2) перерізають призму по чотирикутникам 15, 16, 10, 9 та 13, 17, 18, 14. Визначивши із горизонтальної, та фронтальної проекцій координати цих точок будуємо їх аксонометричне зображення.
ЗАПИТАННЯ ДО ТЕМИ.
1.Як називають аксонометрію?
2.Що таке косокутна і прямокутна аксонометрична проекція?
3.Що таке показники спотворення?
4.Які аксонометричні проекції називають ізометричними і під якими кутами розташавані їх осі координат?
5.Які аксонометричні проекції називають диметричні? Указати показники спотворення у прямокутній диметрії.
6.Як проеціюються кола, що лежать у площинах, паралельних площині проекцій на аксонометричну площину проекції
7.Назовіть розміри малої та великої осі еліпса в диметричній проекції.
8.Назовіть розміри малої та великої осі еліпса в ізометричній проекції.
4
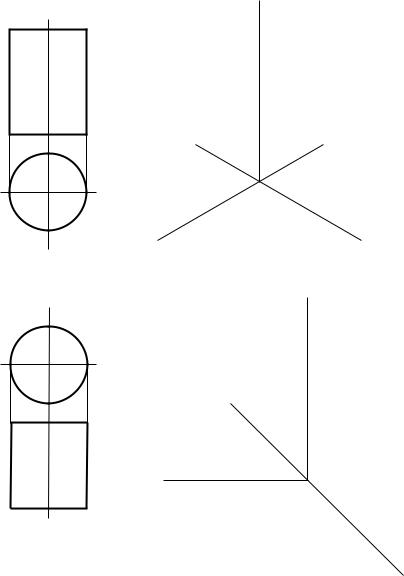
ЗАДАЧІ ДЛЯ САМОСТІЙНОЇ РОБОТИ Побудувати аксонометричне зображення циліндрів.
Z
Х |
У |
Z
X
У
5
ЛІТЕРАТУРА
Базова
1.Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии. М. «Наука»,
1988.
2.Нарисна геометрія. Фольта О.В., Антонович Е.А., Юрковський Б.В. Л. “Світ”, 1994.
3.Бубенников А.В. Начертательная геометрия. – М.: Наука, 1985. – 296 с.
4.Виноградов В.Н. Начертательная геометрия: Учебник. – 2-е изд., пере раб. – М.: Просвещение, 1989. – 239 с.
5.Чекмарев А.А. Начертательная геометрия и черчение: Учеб. пособие для студентов пед. ин-тов. – М.: Просвещение, 1987. – 400 с.
6.Нарисна геометрія: Підручник / В.Є. Михайленко, М.Ф. Євстіфєєв, С.М. Ковальов, О.В. Кащенко; За ред. В.Є. Михайленко. – 2-ге вид., переробл. – К.: Вища школа., 2004. – 303 с.: іл.
Допоміжна
1.Ванін В.В.та ін. Оформлення графічної документації: Навчальний посібник.-К.: Каравела,-2003.-160 с.
2.Посвянский. Краткий курс начертательной геометрии. – М.: Наука, -1979.
3.Посвянский. Сборник задач по начертательной геометрии. – М.: Высшая школа, 1978.- 320 с.
4.Система конструкторської документації. Терміни та визначення основних понять. ДСТУ 3321-96. Держстандарт України. – К. 1996. – 80 с.
5.ЕСКД. Основные положения. М.: Изд-ство стандартов,1984. – 344 с.
6.ЕСКД. Общие правила выполнения чертежей. ГОСТ 2.301-68…2.320-82.
7.Збірник задач з інженерної та комп’ютерної графіки: Навч. посіб. / В.Є. Михайленко, В.М. Найдиш, А.М. Підкоритов, І.А. Скидан; За ред. В.Є. Михайленко. – К.: Вища шк., 2002. – 159 с.: іл.
Інформаційні ресурси
1.Начертательная геометрия. Электронный учебник. Св-во № 2001611308, РОСПАТЕНТ, Москва, 1.10.01 г. [Електронний ресурс]. Режим доступу: http://degispstu.narod.ru/
2.Мультимедийные лекции по начертательной геомтерии / И.Д. Столбова, Е.С. Дударь [Електронний ресурс]. Режим доступу: http://nachertalka.siteeditworld.ru/files
http://nachertalka.siteeditworld.ru/files
3.Библиотека технической литературы. ГОСТы. [Електронний ресурс]. Режим доступу: http://tehlib.com.ua/Gost_1_30.htm
4.Учебник «Начертательная геометрия» / В.А. Лалетин, Е.П. Александрова и др. [Електронний ресурс]. Режим доступу: http://nachertalka.siteeditworld.ru/files
6
